探寻重合本质建构度量模型——《角的度量》教学

陈 慧

【教学内容】

人教版四年级上册第40、41页。

【教学过程】

一、激趣导入

师：（课件出示图1）游乐场里有几个滑梯，你想玩哪个？说说你的理由。

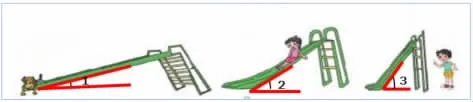
图1

生：我想玩3号，因为这个滑梯最陡，玩起来最刺激。

师：同学们说的陡实际上是指滑板和地面形成的角比较大。（课件抽象出三个滑梯上的三个角）角是我们的老朋友了，关于角，我们都知道什么？

生：角有一个顶点和两条边；角分直角、锐角和钝角。

二、探究新知

1.提出猜想，感知重合。

师：这些角有大有小，如果想知道它们到底有多大，该怎样度量呢？可以用直尺吗？

生：不行，因为尺子是测量物体长度的。

师：（出示图2）我们一起来回忆长度和面积的度量方式。

图2

师：（出示图3）我们在度量长度时，用一小段长度作标准去度量；在度量面积时，用一个小正方块的面积作标准去度量；猜一猜在度量角度时，用什么作标准去度量呢？用什么工具去测量？

图3

生：我猜也是用一个小角作标准去量角，我还听家长说过，可以用量角器来测量角的大小。

师：这节课我们就一起研究用量角器来测量角的大小。（板书：角的度量）

2.梳理问题，初步认知。

师：关于角的度量这节课，你有哪些想知道的？

生：量角器为什么是半圆形的？

生：量角器为什么有两圈刻度？

生：怎样用量角器测量角？

师：请大家带着我们的猜测和问题，自学数学书第40页到41页的内容。

3.互动交流，构建模型。

师：谁来分享你的自学成果？

生：我知道了人们将圆平均分成360份，将其中1份所对的角作为度量角的单位，它的大小就是1度，记作 1°。

（教师播放微课，帮助学生直观建立1度角的表象）

师：（课件演示图4：10个1°角叠加起来）现在10个1°角叠加起来了，这个角是多少度？为什么？

生：这个角是 10°。因为 10个 1°是 10°。

图4

师：（课件演示 2个 10°角叠加成 20°角，3个10°角叠加成30°角）现在这些角又是多少度呢？

生：20 个 1°是 20°，或 2 个 10°是 20°。

生：30 个 1°是 30°，或 3 个 10°是 30°。

师：（课件出示60°的角）估一估，这个角是多少度？

生：估计 50°或 60°。

师：（课件出示图5：依次从60°角不断叠加形成180°角的过程）这里有 180 个 1°角，180 个 1°角叠加起来，形成了一个半圆。观察这180个1°角的顶点，你们有什么发现？

图5

生：这些角的顶点都相交于一点。

师：（出示图6）我们把这个交点称为中心点。为了方便读数，我们给它加上刻度（只出示外圈刻度），刻度为0的线称为0刻度线。

图6

4.画角体验，完善思维。

师：你能在《作业单》的量角器上找出一个刻度为50°的角，并把它画出来吗？

展示作品（展示图7）。

师：能说说你是怎样找到那个开口向右的50°的角的吗？

生：我在量角器上数出了5个连着的10°，就是50°的角。

图7

师：角的开口方向有左有右，以后遇到开口向右的角我们都得10°、10°地数吗？有没有什么好办法？

生：可以在量角器上增加一圈刻度。（课件演示增加内圈的刻度）

师：现在谁能说说为什么量角器有两圈刻度？

5.辩论化错，突破难点。

师：现在我们已经能在量角器上找角、画角，还能读出它的刻度，你会用量角器测量角吗？独立尝试测量作业单上角的度数。

（展示学生作业单）

生：1号是错的，因为量角器的0刻度线没有和角的一条边重合。

生：2号也是错的，因为量角器的中心点没有和角的顶点重合。

生：3号读数错了，应该从0刻度线所在的那一圈刻度读起，应该是读内圈刻度，是50°。

生：4号是正确的测量方法。

师：现在谁来说说怎样测量角的大小？你特别想提醒同学们注意什么？

生：量角器的中心点要和角的顶点重合，量角器的0刻度线要和角的一条边重合，再观察另一条边所对的刻度。我要提醒同学们读数时要正确选择内圈或是外圈的刻度。

展示四位同学的作业单，全班交流，明晰相应的操作流程，在辩论化错的过程中帮助学生逐渐梳理出用量角器度量角的方法，并进行归纳提炼：三个重合。特别通过对3号作品错误方法的反复说理，突破难点——读数时，要特别关注被测量的角的一条边是对准内圈还是外圈的0刻度线。

三、收获与延伸

师：这节课你有什么收获？在高年级，我们将会研究如何度量一个物体所占空间的大小，也就是物体的体积，有兴趣的同学下课后可以接着想一想！