关注本质夯实概念——《倍的认识》教学设计（一）

殷 芊

【教学内容】

苏教版三年级上册第4、5页。

【教学过程】

一、直观感知，找准思维生长的起点

师：公园有许多美丽的花朵，你能数一数吗？

预设：蓝花有2朵，红花有6朵。

师：根据学过的知识，你能提出哪些数学问题？

预设：两种花一共有多少朵？红花比蓝花多多少朵？蓝花比红花少多少朵？

师：我们可以把这三个问题分一分类，怎么分？

预设：第一个问题是求和，用加法解决。第二个和第三个问题都是在比较两个数量，用减法解决。

师：同学们，对两个数量进行比较，除了比较多少，还有一种比较方法，今天我们就来学习这种特别的比较方法。

【设计意图：引发学生自己提出数学问题，唤醒其原有的认知结构，运用差比的关系比较两个数量，这是学生思维的起点。“倍”的产生也源于比较，它是另一种比较两个数量关系的方式，从“比多少”的比较到“倍的认识”的比较是一个质的飞跃。】

二、操作体验，建立“倍”的概念本质

1.交流分享，引出“倍”。

师：同学们，像这样把2朵蓝花圈起来看作1份（边说边圈），那红花有这样的几份呢？让我们一起圈一圈。

演示：

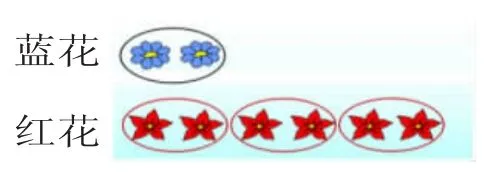
小结：蓝花有2朵，红花有3个2朵，我们就说红花的朵数是蓝花的3倍。（板书）

2.对比分析，认识“倍”。

师：红花又开了2朵，现在红花的朵数是蓝花的几倍？能用圈一圈的方法解决吗？在练习纸上试一试。

师：为什么要2个2个地圈？

预设：因为要把2朵蓝花看作1份。

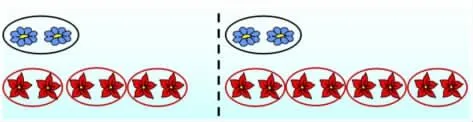
对比：仔细观察这两幅图，怎么一眼看出第一幅红花的朵数是蓝花的3倍，第二幅红花的朵数是蓝花的4倍？

预设：有3个圈表示有这样的3份，也就是3倍。有4个圈表示有这样的4份，也就是4倍。

3.突出变化，理解“倍”。

师：蓝花的朵数变成了4朵，现在红花的朵数是蓝花的几倍？

展示错例：

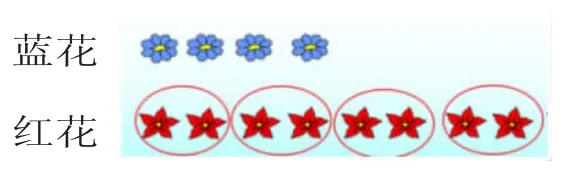
指出：要根据蓝花的朵数来圈，蓝花有几朵，就几个几个地圈。

对比：红花的朵数没有变，为什么刚才红花的朵数是蓝花的4倍，现在红花的朵数却是蓝花的2倍呢？

预设：左边的红花和2朵蓝花比，8朵红花里有4个2朵；右边的红花和4朵蓝花比，8朵红花里有2个4朵。

小结：同样是8朵红花，但蓝花的朵数变了，也就是一份数变了，标准就变了，倍数也就改变了。

【设计意图：教学注重在动态变化中厘清对倍的认识，让学生经历了两次对比和抽象的过程，第一次先固定每份数不变，变化几份数，让学生对比倍数的变化，成功建立“倍”与“几个几”之间的关联；在前面几次都是蓝花的朵数不变，学生充分认识到“把2朵蓝花看作1份，有几个2朵就是蓝花朵数的几倍”之后，第二次变化每一份数，对比倍数发生的变化，成功制造了认知冲突，引发学生再一次深入地思考，丰富了“倍”的表象，突出强化了对标准量的理解，让学生在变与不变中充分理解“倍”。】

三、提升经验，沟通“倍”的联系

1.沟通与除法的联系。

师：同学们真棒，能够从相似的图中找出不同之处，接下来请你们开动脑筋，要求红花的朵数是蓝花的几倍，可以怎样计算？选择一幅图自己研究。

预设：6÷2=3（倍），8÷2=4，8÷4=2。

师：为什么用除法来计算？

预设：想红花里面有几组这样的蓝花，8里面有几个4，所以用除法。

师：注意，倍是表示两种数量之间的关系，所以不写单位名称。

小结：我们要知道一个数是另一个数的几倍，不仅可以圈一圈，还可以用除法来计算。

2.整体把握倍的意义。

课件出示要求：摆出的红花的朵数是蓝花的2倍。

师：摆的红花、蓝花的朵数各不相同，为什么红花的朵数都是蓝花的2倍？

师：如果是摆小棒呢？怎样摆才能使得第二行小棒根数是第一行的2倍？

小结：这就是我们今天学习的“倍”的知识。

【设计意图：给予学生充分研究的空间，基于图示表征下对“倍”概念的理解，自主探究新知“倍”与旧知“除法”的内在联系，感悟“倍”的本质，即表示的是两个量之间的关系。让学生的思维逐渐过渡到算式表征，抽象对倍的概念的理解。在摆花片环节，精心设计逆向思维任务，已知倍数关系，如何确定标准量、比较量？在交流过程中，学生不难发现这里摆出的红花、蓝花朵数各不相同，在“你变我也变”之中依然存在着不变的那条线，帮助学生系统地把握“倍”的本质。】

四、深化认知，促进思维延展

1.画一画，比一比。

出示要求：

师：请同学们画一画，你想创造出几倍？和你的同桌分享。

预设：我画出来的第二行是第一行的4倍，第一行画了3个圆，第二行画了12个圆。

在采访中，他常常爽朗地大笑着，说起他们每到一处，就四处打听哪里有带花纹带文字的石头，拎着墨汁就去了。因为在某单位厕所里拓汉画石像时间太久，挨了如厕人的骂。他们被那些精美的线条、图案所感染，根本意识不到时间的流逝、也忘记了环境的香臭。人家骂得火冒三丈，他们拓得心满意足：你们上你们的厕所，我们拓我们的拓片，互不影响互不影响。

预设：我创造出了1倍。第一行画了1个三角形，第二行画了1个正方形。

师：当两个量相等时，它们之间还存在着一种特殊的倍数关系。

2.猜水果。

哪一箱是苹果？哪一箱是梨子？

师：我这里有三个箱子，猜一猜哪一箱是苹果？哪一箱是梨子？

线索一：苹果的个数是梨子的2倍。

预设：可能①号箱是苹果，②号箱是梨子；也可能②号箱是苹果，③号箱是梨子；③号箱肯定不是苹果。

线索二：苹果和梨子的个数相差2个。

预设：只能②号箱是苹果，③号箱是梨子。

3.装球游戏。

师：可以怎样装球，使第一个口袋里的个数是第二个口袋里的2倍？

预设：一共要把这12个球装完，我可以分几次装，每一次都在第一个口袋里放2个，在第二个口袋里放1个，直到放完为止。

预设：要使第一个口袋里球的个数是第二个口袋里的2倍，可以用画图的方法。把第二个口袋里的球看作1份，第一个口袋里就有这样的2份。所以12个球就是 3份的总和。12÷3=4（个），就是第二个口袋里球的个数。

【设计意图：创造性地使用教材，放手让学生自己创造“倍”，突出学生个性化的对“倍”概念的本质特征进行表征，给学生提供参与几何直观活动的机会，积累用图示学习数学的经验。思维发展的载体随着游戏形式不断变化，将两种比较的途径融进猜水果游戏中，将“差比”与“倍比”共生，再次激活学生对新知与旧知联系的认知。在装球游戏环节，渗透“和倍问题”的解决策略，借助已有的情境图，让学生在实际操作中感受策略的多样性，尝试利用“比较量÷标准量=倍数”模型进行逆向思考，让学生的思维向更深处延展。】

五、全课小结

师：同学们，今天我们认识了“倍”，你知道了什么？