基于RGARCH-Copula模型的中美股市尾部相关性研究※
郭云康 吴鑫育 侯信盟
(安徽财经大学,安徽 蚌埠 233030)
一、引言
相关性分析在金融分析中具有非常重要的作用。在产品定价、波动溢价研究、评估投资组合绩效、风险管理研究等领域中,相关性的研究均有涉及。伴随着全球化进程的推进,世界金融经济的发展衔接越来越紧密,尤其中国金融的发展,在世界范围内都有着举足轻重的地位。近年来,中国金融市场迅速发展,与各国股市间的相关性程度也在不断的加强。在各国金融市场中,美国股市是最为发达的股市,鉴于中美两国经济越来越密切,因此,从相关性分析的角度来研究中美股市就显得尤为必要。
近年来,已经有部分学者对于中美股市相关性进行研究。其中,张兵等(2010)中美股票市场的联动性研究指出美股收盘收益率对上证开盘收益率的影响呈现U型曲线,在极端条件下美股变动对中国股市的冲击较为显著[1]。赵喜仓,董小亮(2011)在股权分置改革前后中美股市相关性比较分析中指出在我国股权分置改革之前,中美股市的相关性不强,但是随着我国股权分置改革和QFII的引入,中美股市的相关性越来越大,中国股市将更大程度地受到美国股市的影响[2]。刘伟江等(2015)宏观经济与中美股市动态相关性研究中表明自QDII出台后中美股市相关性进入了一个相对平稳的上升通道,但经济危机爆发时相关性却表现出短期下降后迅速增加的走势[3]。
而伴随着计算机的迅猛发展,对于Copula理论的研究更加深入,Copula函数逐渐成为相关性研究领域极为重要的工具。不仅如此,Copula的研究还更多地与其他模型相互组合,更精确化地定量分析各种金融资产之间的相关性。本文从GARCH模型与Copula模型组合角度出发,来研究中美股市尾部相关性。在此之前,许多学者已经作出很多研究。Embrechts等(1999)开创性的将Copula模型应用到了金融风险分析领域内,为后来人们的应用提供了很好的参考[4]。Dias等(2003)在金融时间序列模型GARCH模型的基础之上,将Copula函数与GARCH模型相结合使得GARCH模型比单独使用的时候其结果更能准确的刻画金融时间序列之间的相关性关系[5]。Roch等(2006)构造了ARMA-GARCH边缘分布模型,选取西班牙股票市场的数据进行研究,并利用最小方差检验法选出了对金融时间序列拟合程度较高的Copula函数,从而通过Copula函数来研究不同股票市场之间的相关关系[6]。Jondeau和Rockinger(2006)通过实证分析建立了有条件的Copula-GARCH模型,当回报与反向移动时相比,相关性会受到更大的影响[7]。杜方欣等(2013)通过建立两个时间序列模型GARCH-GED和EGARCH-GED,用这两个模型计算边缘分布,运用混合Copula函数分析金融市场中收益率的相关性[8]。徐映梅等(2013)通过Copula-GARCH-t模型对中国沪深A股指数和恒生指数的收益率和联动性特征进行了分析[9]。张学功等(2016)提出Pair Copula-SV-t模型来度量金融资产间的相关性,该模型在运用SV-t模型度量边缘分布的基础上,通过Pair-Copula方法来得到高维联合分布[10]。基于已实现测度理论,Hansen、Huang和Shek(2012)提出在传统GARCH模型中引入已实现测度,即RGARCH模型,用来刻画已实现测度波动情况以及其对条件方差的影响。Realized GARCH不仅有杠杆效应,还能够描述波动率的非对称效应[11]。
由于中美股市相关性研究的文献较少,传统GARCH模型与Copula模型组合研究相对成熟,相比传统GARCH模型,RGARCH模型对于高频数据的处理能够利用更多的市场信息,更好的滤过波动率,从而提高模型估计精确性。因此,在此基础上,本文采用RGARCH模型与Copula模型相结合的形式对中美股市的尾部相关性进行研究。不同于传统的GARCH模型与Copula模型的组合,本文是先利用RGARCH模型对资产收益率过滤,而后通过累积分布函数的转换,得到Copula模型的边缘分布函数,最后利用极大似然函数估计中美股市尾部间的相关性。这种选择能够比传统Copula-GARCH模型更准确的提取市场间的相关性信息,对于尾部相关性的度量具有重要意义。
二、RGARCH-Copula模型
(一)Copula
Copula函数是一种将单变量分布函数连接在一起形成一种多元分布函数,它反映着变量之间的依赖关系。Copula也可以解释为“相依函数”或“连接函数”,是把多维随机变量的联合分布用其一维边际分布连接起来的函数。我们可以将金融资产分解成单个资产和投资组合两部分,其中单个金融资产可以由它们各自的边缘分布来描述,而投资组合则完全由连接它们的Copula函数来描述。
假设一个向量随机变量X=[X1,X2,…,Xn]',联合分布函数为F,边际分布函数分别为F1,F2…,Fn,根据sklar’s定理,可以得出copula函数:
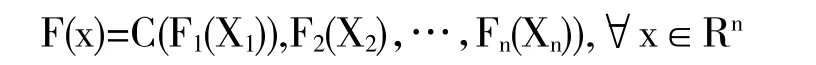
对于任意多元分布F,都可以将其分解成边缘分布Fi和一个copula函数。
周梅,樊毅斌(2017)指出GARCH模型能够较为精确地描述金融时间序列的尾部分布特征,并且认为收益率方差是可预测的。由于不同的金融资产收益率序列可能具有不同的边缘分布,因此,可以利用GARCH模型得到时间序列边缘分布,再利用Copula函数对概率积分变换后的时间序列进行连接,以此来描述中美股市间收益率之间的相关结构[12]。
(二)RGARCH模型
模型RGARCH(p,q)具体形式如下:
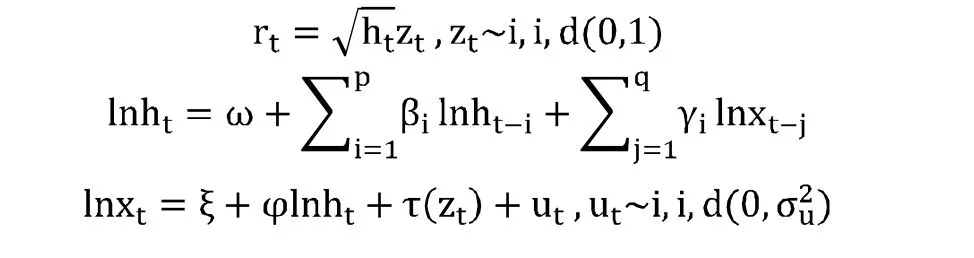
其中,rt表示日对数收益率,ht=var(rt|Ωt-1)为收益率的条件方差,xt为已实现测度。一般情况下,zt与ut相互独立。τ(zt)为杠杆函数,本文将τ(zt)设定为以下二次形式:
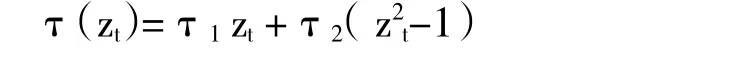
为了更好地刻画收益波动的杠杆效应,从而解释收益波动的非对称特征,因此在上述RGARCH模型的基础上引入新的参数。
(三)IFM(两步估计法)
实际中比较常用的Copula估计方法是两步估计法(IFM),IFM方法比EML方法估计更有效,由joe(1997)提出,他证明了在正则条件下,IFM所得参数会依分布收敛于真实参数。这种方法是一种两步最优化的方法,要求边际分布中参数和Copula参数是可以分开的(龚玉婷(2015)金融资产相依性的动态Copula建模及应用)。因此,先估计边际分布模型中的参数[13]:
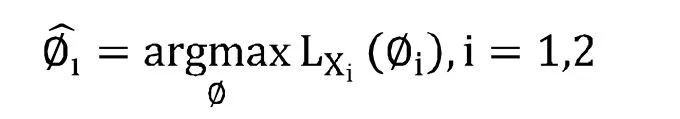
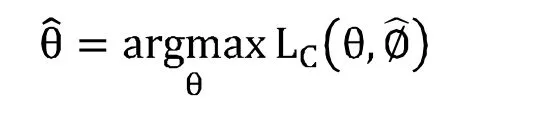
可以看出,用IFM方法将边际分布参数和Copula参数估计分离开来处理,能够减少运算量。
三、实证分析
(一)样本选取
本文采用中国上证综合指数和美国标普500指数日收盘价数据和基于5min高频数据构建的已实现测度作为研究样本。数据抽样的时间跨度为2010年1月4日到2018年9月28日,两种指数均有2058个数据,数据来源于Oxford-Man Institute of Quantitative Finance数据库。本文对两指数日收盘价对数化处理,分别算出对数收益率r1t、r2t,对应的计算公式为:rit=(lnpit-lnpit-1),i=1,2,从而得到日收益率序列retsse={r1t},retspx={r2t}。其中,Pit为第i个指数第t个交易日的收盘价格。两指数已实现测度分别记为RVsse、RVspx。表1给出了上证综合指数与实证成分指数对数日收益率的描述性统计结果。
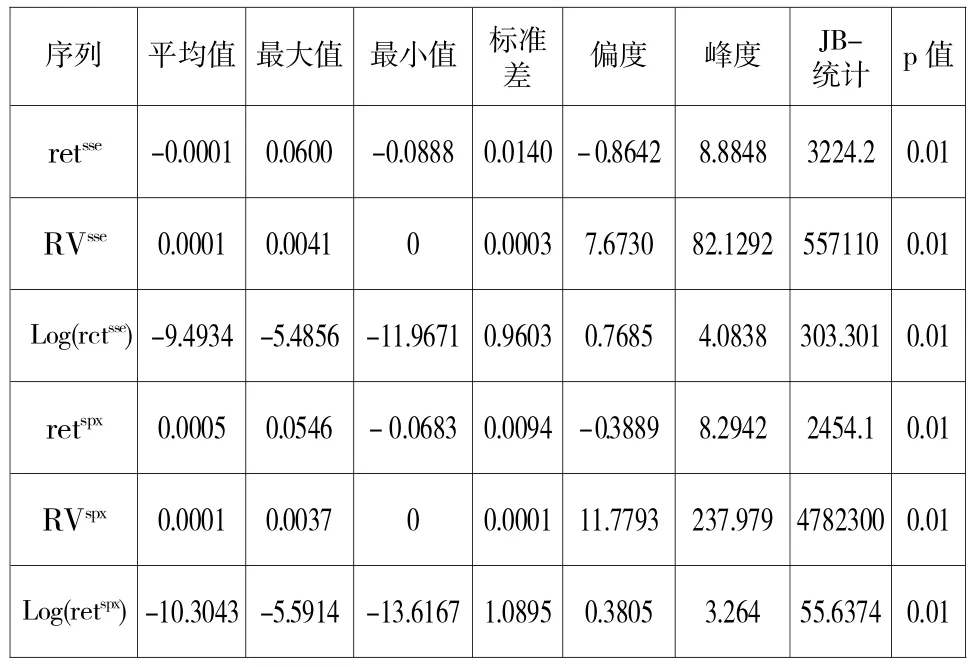
表1各序列的描述性统计特征
从均值来看,上证综指的对数收益率呈现负的平均收益率,而标普500指数对数收益率呈现正的平均收益率;从最大值与最小值来看,标普500指数与上证综指的收益率较为接近。因此,从这两点可以看出,美国金融市场强于中国金融市场。从已实现测度均值来看,上证综指和标普500指数均为正数,且都为0.001;从最值来看,其最大值与最小值非常接近,说明两指数日内高频交易波动相近。
从偏度来看,上证综指对数收益率的偏度为-0.8642,而标普500指数对数收益率的偏度为-0.3889,这表明两指数均有较长的左偏现象,且上证综指更为明显;从峰度来看,上证综指对数收益率的峰度为8.8848,标普500指数对数收益率的峰度为8.2942,说明两指数呈现尖峰形态。综合来看,这正是金融时间序列中常出现的尖峰厚尾现象。图1是两指数对数收益率的频率分布直方图。从图中我们能够清晰直观的看到这种现象。
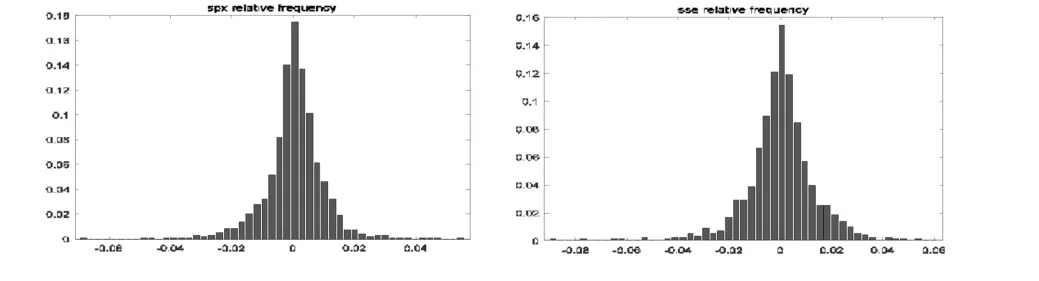
图1上证综指和标普500指数对数收益率的频率分布
而对于两指数的已实现测度对数化处理后,其偏度与峰度明显降低,说明对数化后的已实现测度更加接近于正态分布。从Jauque-Bera统计量看,P值均为0.001,说明上述序列均拒绝服从正态分布的假设。因此,可以通过RGARCH模型在已实现测度的条件下对两指数收益率残差序列进行过滤。图2反映了两指数收益率的波动情形。
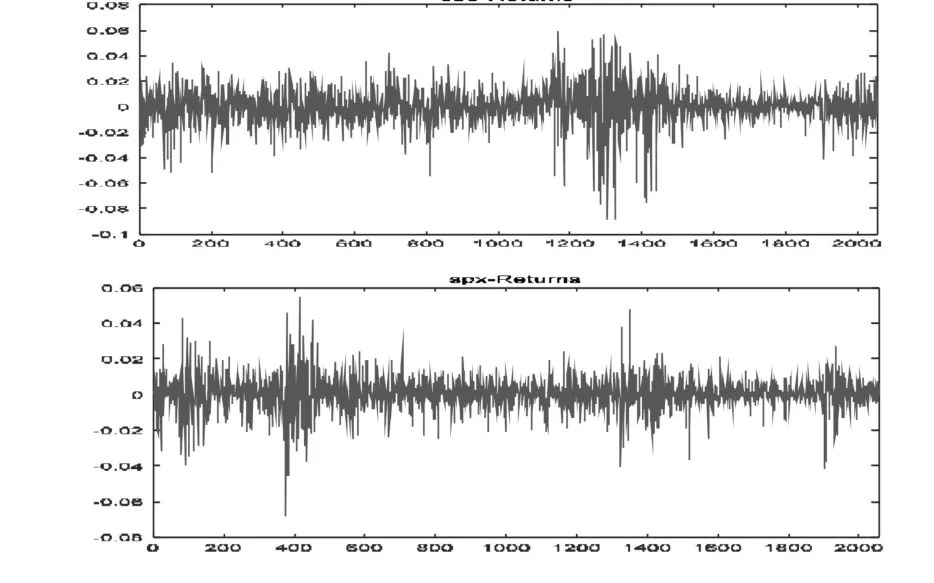
图2上证综指和标普500指数收益率的波动情况
从图2可以看出两指数收益率呈波动集聚效应,即大的波动之后出现大波动的可能性更大,反之亦然。而RGARCH模型是在已实现测度的条件下进行估计,同时,已实现测度的分布接近于正态分布。因此,采用RGARCH模型对数据进行过滤要优于传统GARCH模型。
(二)RGARCH模型估计结果
鉴于许多学者对GARCH类模型做了许多实证研究,因此,利用GARCH类模型作估计时,一般从两个方面考虑:一是GARCH类模型的滞后阶数选取;二是残差分布的选择。本文采用的RGARCH模型估计的一阶形式,对应的残差分布是正态分布,在对已实现GARCH模型进行建模时,采用的是5min的已实现测度。表2是RGARCH模型估计的参数表。
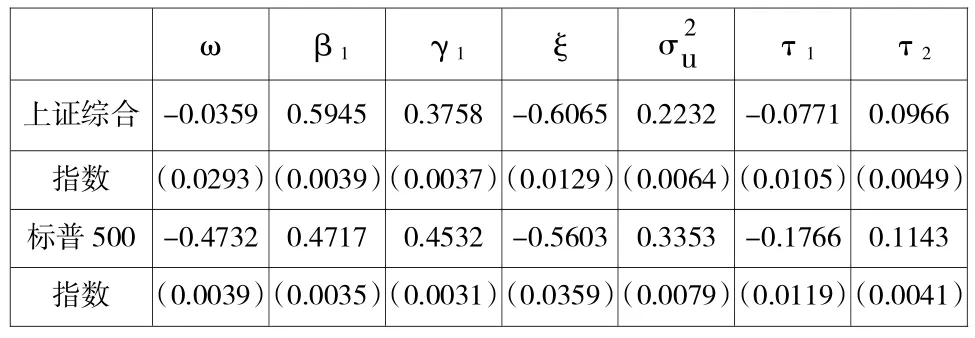
表2 RGARCH模型估计的结果
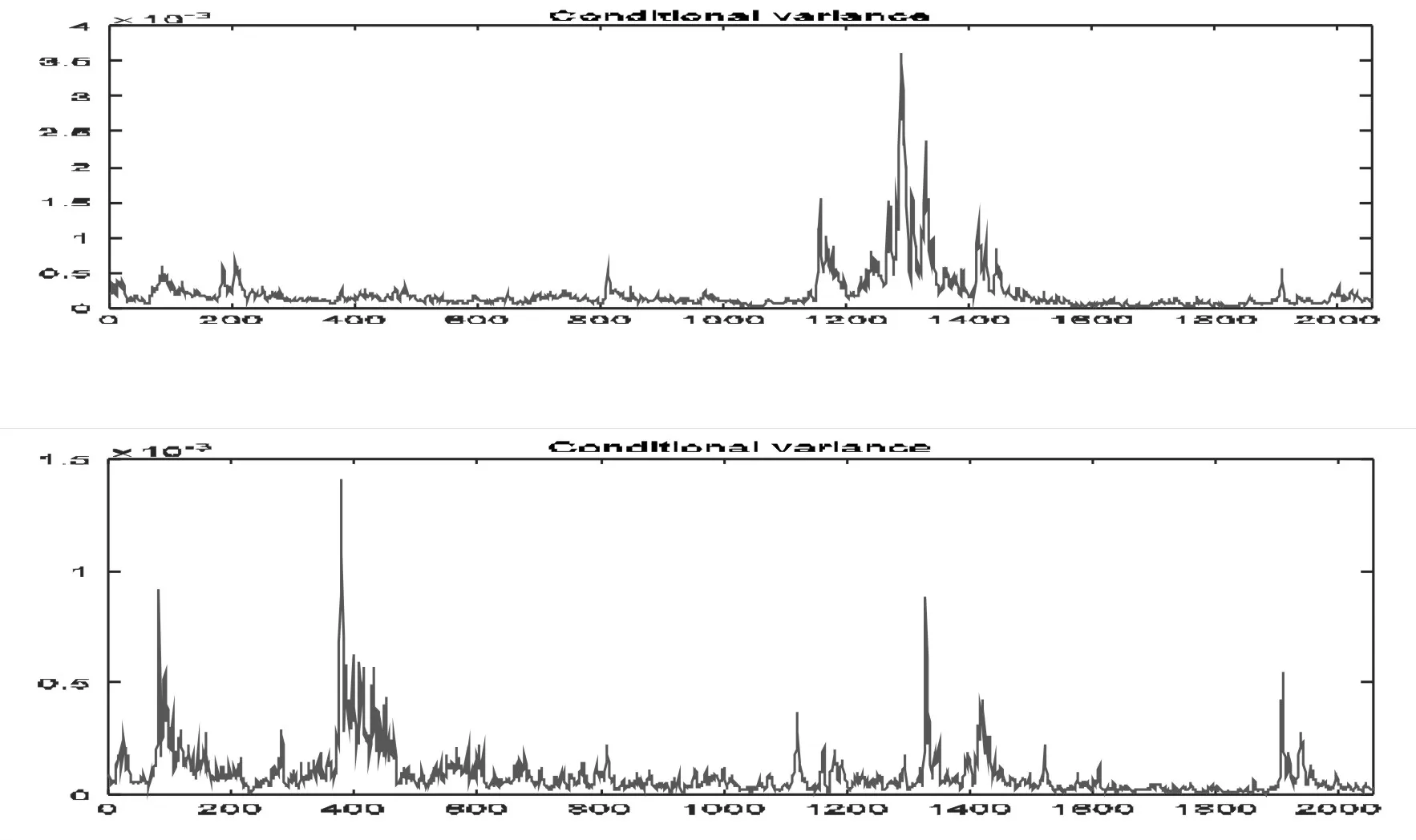
图3上证综指和标普500指数条件方差的波动情况
由表2可知,在5%的显著性水平下,通过RGARCH模型估计后的各个参数都是显著的。两指数估计后的值均为正,说明两指数的收益率波动与历史波动存在一定的正相关关系。此外,为负,为正,说明两指数收益率存在明显的杠杆效应。从图3中可以看出,上证综指和标普500指数的条件方差有着明显的时变性和波动率聚集的特征,所以对两市场相关性进行度量时,应充分利用已实现测度,即利用RGARCH模型进行过滤,而后运用copula函数进行有效估计,以便能更加有效衡量两市场之间的相关性,继而对相关性风险的度量提供借鉴意义。
(三)Copula模型估计
金融时间序列中常用的Copula函数有很多,为此本文选取 Gaussian Copula、Student-t Copula、Gumbel Copula、Survival Gumbel Copula、Clayton Copula、SurvivalClaytonCopula、SJCCopula等7个Copula函数进行拟合,然后根据最小似然值以及AIC、BIC准则进行选取最佳Copula函数,而后对于选取的最佳Copula函数做时变处理,观察市场尾部间的动态相关性。
一般而言,Gaussian Copula函数能够很好刻画变量间的相关性。但由于它的密度函数具有对称的特征,使其不能对金融资产间的非对称相关性进行描述。Student-t Copula与Gaussian Copula相同,其密度函数也呈现出对称的特征。两者在对金融资产间所出现的对称相关性进行刻画方面,均能取得较好的效果。但是,t-Copula函数具有更厚的尾部,因此常用于刻画尾部相关性。而Clayton Copula函数的密度函数不仅呈现出非对称,而且还具有下尾高、上尾低的特征。它可以很好地捕捉到下尾部依赖性的情况,即,当市场处于下跌趋势时,它可以对资产间的相关性进行有效刻画。因此,不管是当金融资产间的相关性程度比较强的时候,还是其处于下跌情形,有极端风险发生时,Clayton Copula函数都能对其进行准确的描述。对于Gumbel Copula来说,其密度函数同样呈现出非对称的特点。然而,它和Clayton Copula恰恰相反,表现为下尾低、上尾高的特点。所以,Gumbel Copula函数可以有效刻画金融资产间的上尾相关性。Survival Gumbel Copula和Survival Clayton Copula分别只能描述下尾和上尾的相关性。
关于SJC Copula,考虑到金融时间序列中波动可能同时存在上下尾相关性,且具有非对称特征。所以,在相关性的度量中引入该Copula函数非常有必要,对应的上尾记为λU,下尾记为λL。其他各种Copula函数尾部相关性的表达式(见吴鑫育(2018)中国股票市场的波动率聚集性研究)[14],如表3所示:
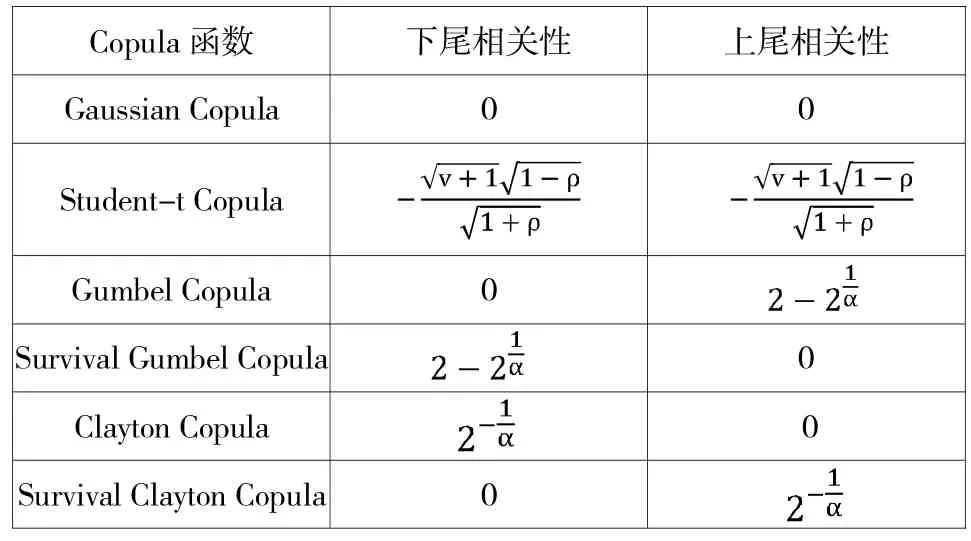
表3各种Copula函数尾部相关性表达式
应用两阶段极大似然估计法来估计各类Copula函数的参数。第一阶段,对两指数的收益率的波动利用RGARCH模型估计,转换为边缘分布;第二阶段,将得到的边缘分布分别代入各个Copula函数中,进行参数估计。
在第一阶段中,本文上述对上证综指和标普500指数收益率系列已经利用R-GARCH模型进行过滤,而后准备采用Copula模型来度量中国股市和美国股市尾部间的相关性。通过R-GARCH模型估计后,对两指数的残差收益率序列利用经验累计分布函数进行转化,得到对应的时间序列边缘分布。图4为两指数的收益率经验分布图,从图中可知,上证综指的收益率经验分布与标普500指数收益率经验分布极为相似,对于两市尾部相关性提供了可靠依据。
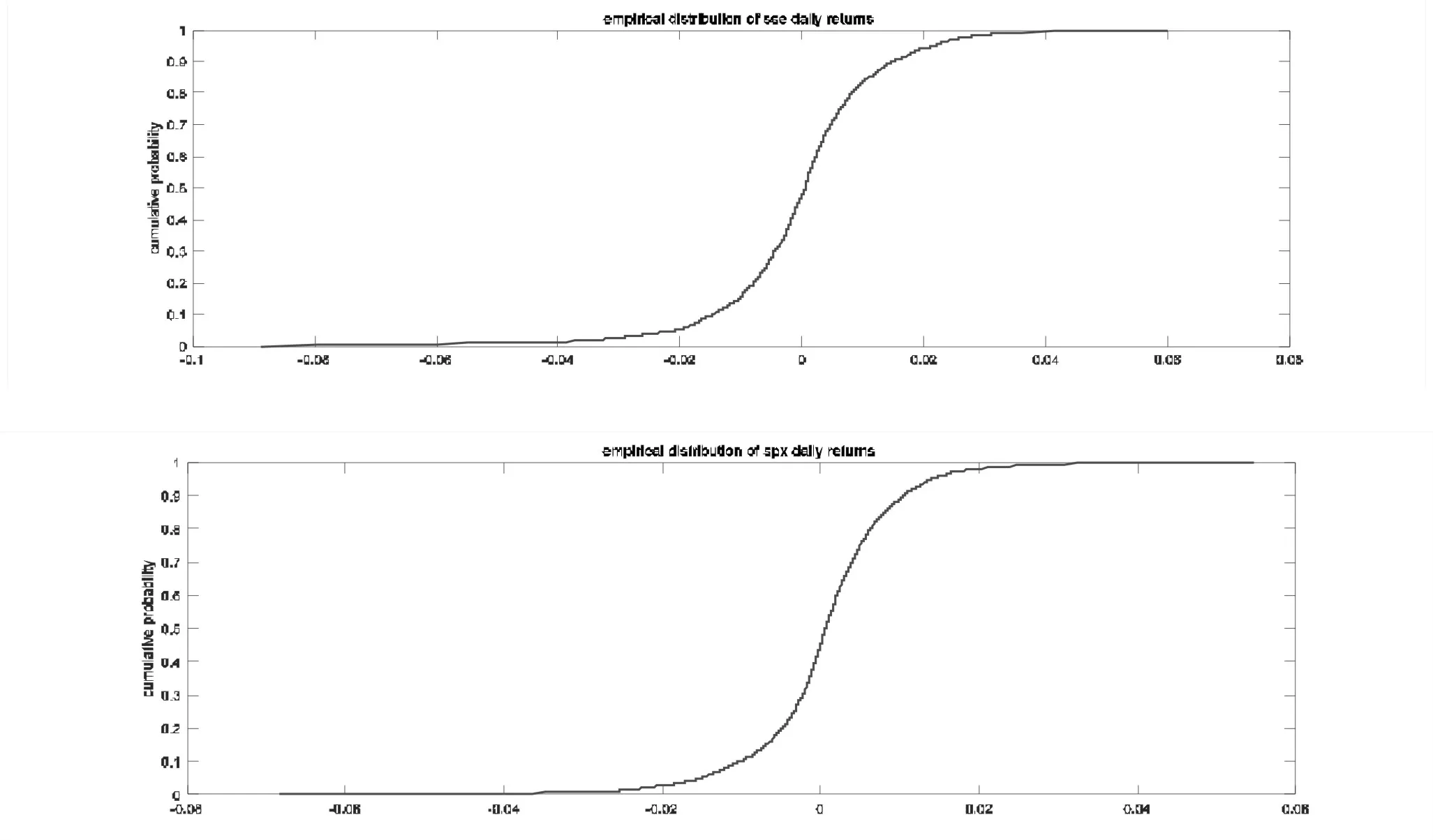
图4上证综指和标普500指数的日收益率的经验分布
根据第一阶段由R-GARCH模型过滤后转化的的边缘分布,采用极大似然法得到各个Copula参数的结果如表4所示。由表4可知,所有Copula函数估计的参数值均显著,说明中国股市和美国股市在波动上呈现着线性或非线性相关性。从表4的对数似然值的比较来看,SJC Copula表现最优,拟合度最好;其次,Survival Gumbel Copula的拟合次于SJC Copula,效果依旧很好;再次,Student-t Copula和Clayton Copula拟合程度还不错。基于AIC和BIC的信息准则可以看出,Survival Gumbel Copula的拟合效果最好,而SJC Copula次之;其次,拟合程度较好的是Clayton Copula。SJC Copula能够同时描述下尾和上尾相关性,从SJC Copula参数结果可知,下尾相关性为0.0214,上尾为0。综合来看,不论是Survival Gumbel Copula还是SJC Copula,都对下尾相关性的描述较好,说明两股市尾部波动具有非对称特征。
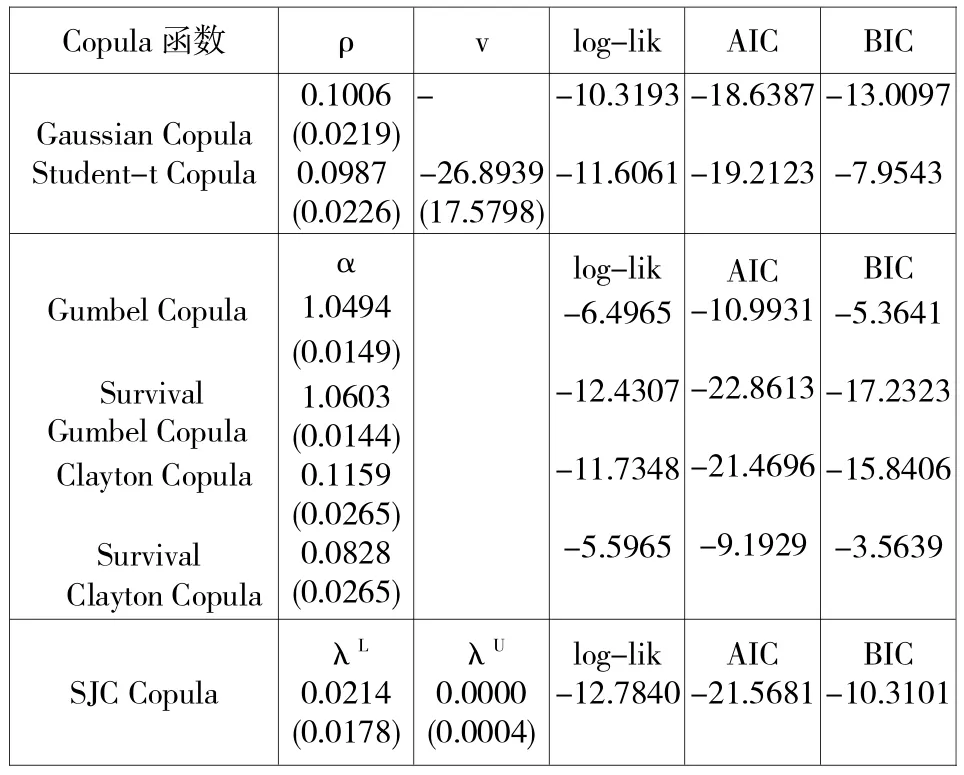
表4Copula参数估计结果
在金融市场中,从经验角度来说,当美国股市大涨的时候,中国股市未必会涨;当美国股市大跌的时候,中国股市会伴随着下跌。从实证结果来看,SJC Copula对两市场双尾部进行度量,得出两市场具有下尾相关性,而上尾相关性为0,这种情况也正是契合了现实中的股票市场,美股下跌情绪的传染要高于美股大涨的时候。
从各种Copula参数估计结果中,了解到了两股市下尾具有一定的相关性。为了更确切的了解这种情况,从对数似然值与AIC和BIC信息准则的角度来看,对于各个静态Copula估计中得出最佳Copula函数(即Survival Gumbel Copula和SJC Copula)做时变估计,进一步度量尾部间的动态关系。因此,时变SJC Copula和时变Survival Gumbel Copula参数估计结果如表5所示。
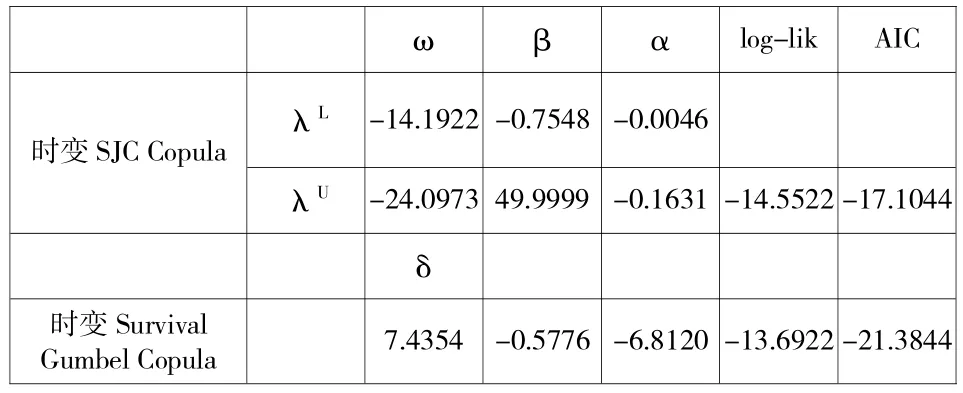
表5 时变Copula模型的参数估计
由AIC准则可以看出,时变Survival Gumbel Copula函数拟合要比时变SJC copula函数更优一些,不论从对数似然值还是AIC准则来看,时变SJC copula都要比SJC copula的效果差很多。时变Survival Gumbel Copula函数估计图像如图5所示。
图5 时变Survival Gumbel Copula函数估计波动情况
Survival Gumbel Copula函数能够很好地捕捉中美股市间的下尾相关性,而时变Survival Gumbel Copula函数能够更加精确的描述下尾间的动态关系。从图5中可以看出,中美股市间的尾部相关性随着时间变化波动较大,这也正反映了股市波动的实际情况,说明中美股市间极端下跌的风险也是动态变化的。
四、结论
本文利用RGARCH-Copula模型对2010年1月4日到2018年9月28的上证综指和标普500指数收益率进行研究。具体来说,利用R-GARCH(1,1)模型对两指数的收益率进行过滤,结合IFM方法转换为Copula模型边缘分布,接着建立了Gaussian Copula、Student-t Copula、Gumbel Copula、Survival Gumbel Copula、Clayton Copula、Survival Clayton Copula、SJC Copula等 7个静态Copula函数以及时变Survival Gumbel Copula和时变SJC Copula进行拟合,并通过对数似然值和两种信息准则的比较,选出最佳Copula模型,继而对两市场尾部的相关性进行分析。
静态Copula模型的分析中得出,Survival Gumbel Copula和SJC Copula模型相对较优,Survival Gumbel Copula能够很好的描述下尾相关性,不能对上尾相关性进行描述,而SJC Copula可以描述同时存在上尾和下尾的情况,两者结合来看,两个市场尾部相关性中下尾较为明显,因此,说明两市场同时发生极端下跌的可能性较大。在时变相关性分析中,时变Survival Gumbel Copula函数拟合较好,相关系数随着时间的变化而有所波动,说明两市场下跌情绪传染较为明显,其相关性具有一定的动态特征。

