挖掘数学文化 提升数学素养*——基于两堂“两角差的余弦公式”课的评析与反思

●黄慧军

(瑞安中学,浙江 瑞安 325200)

前不久，笔者观摩了两节同课异构，内容是“两角差的余弦公式”第一课时，其中甲与乙两位教师不同的教学设计折射出不同的教学理念，引起了听课教师的争论.笔者重新研究课程标准与教材编写意图，得到一些思考与启发，与大家分享.

1 案例背景

“两角和与差的余弦公式”是本章的起始课，是三角恒等变换的基础，也是后续学习两角和与差的正弦、正切的知识基础和方法源泉.这节课的教学重点与难点是两角和与差的余弦公式的产生和推导.

2 案例概述

案例1

问题1 填空求值：

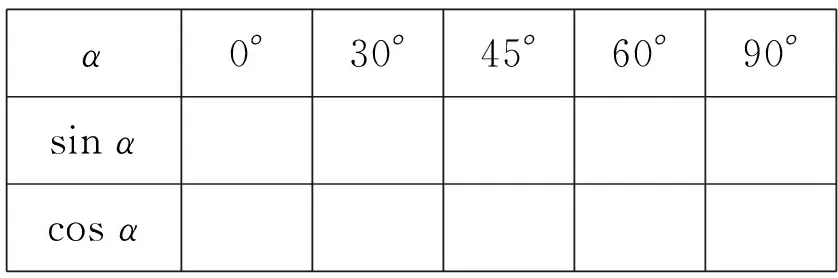
α0°30°45°60°90°sin αcos α

问题2 cos 15°能求吗？

学生想到cos 15°=cos(60°-45°)，猜想:

发现不对.教师甲未加评析，显示问题3：

问题3 如何用α,β的正、余弦值来表示cos(α-β)？

在教师的引导下，学生想到用单位圆中的三角函数线来表示.由于学生不了解公式的结构特点，无法进行下一步推进，陷入僵局.然后教师使出“全身招数”，学生一路“磕磕碰碰”.教师甲用了半个多小时完成了公式的推导，然后告诉学生公式只能在α,β,α-β都是锐角，且α>β的情况下才成立的,要想推广到任意角，还得做不少的工作.最后教师甲用不到5分钟的时间匆匆地介绍了教材上的向量推导法，下课的铃声就响起来了.

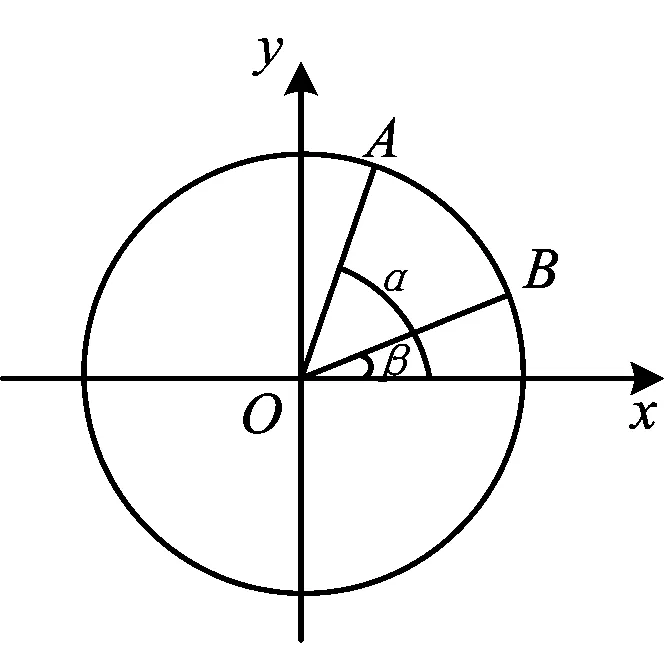
图1

案例2 教师乙通过教材必修4中的习题引入：如图1，在平面直角坐标系中，以原点O为圆心、单位长度为半径的圆上有两个点A(cosα,sinα)，B(cosβ,sinβ),试用点A,B的坐标表示∠AOB的余弦值？

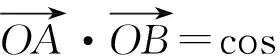
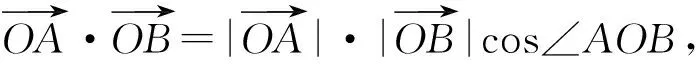
得cos∠AOB=cos(α-β)=cosαcosβ+sinαsinβ.

教师乙追问：

问题1 请你利用本题的结论求cos 15°？

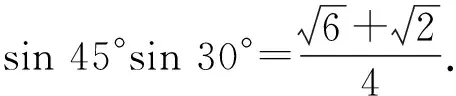
问题2 当α,β为任意角时，cos(α-β)=cosαcosβ+sinαsinβ还成立吗？

学生找到了关系∠AOB=α-β-2k1π或∠AOB=α-β+2k2π，其中k1,k2∈Z,从而cos(α-β)=cos∠AOB=cosαcosβ+sinαsinβ成立.

得出公式后，教师乙通过数学史，找价值、看证明,介绍了2世纪古希望天文学家、数学家托勒密利用托勒密定理得到的相当于两角和与差的正、余弦公式的结果，制作了现存最早的弦表(从0°到90°每隔半度比较精确的正弦函数值).接着介绍了3世纪末古希腊数学家帕普斯在《数学汇编》中为三角公式的证明提供的几何模型，最后讲解例题，对公式进行应用.

3 案例评析

案例1是从如何求cos 15°引出，遗憾的是教师甲没有进一步引导学生对cos(60°-45°)的展开式进行猜想，更不说一般性的猜想了.这样一来，学生就不清楚公式的结构特点，导致推导一般情况时思维受阻，教学进度受影响.另外，采用的几何法让学生倍感突兀，很难接受.因为从教材的编写来看，虽然教材之前介绍了三角函数的几何表示，但是后续涉及很少，导致学生很难想到将某个角的三角函数值用单位圆中的线段来表示.从教学效果来看，教师甲显然没做到精准教学.

案例2是从教材上的一道习题引入，突出了“向量的数量积公式”，让学生体会到向量方法的作用及向量与三角函数的关系，为后续的公式推导提供了方法.在公式推导成功后，教师乙再向学生梳理了两角差余弦公式的产生与发展过程，让学生感受到两角差余弦公式产生的必要性.把教材中的几何法(帕普斯模型)穿插在数学史中由师生共同来完成，让学生明白教材中之所以先选用几何证法是符合差角公式的历史发展顺序的，是人们认识差角公式的历史发展写照，整个教学过程有比较浓厚的文化气息.不过，本节是公式探究课，要让学生体验和感受公式发现的过程，因此在引入部分要给学生思维的空间，不能把向量方法看成唯一的思路，这是案例2的遗憾之处.

4 案例反思

目前随着核心素养的提出，发展学生的数学核心素养成为数学教育追求的真谛.而数学文化与数学核心素养是相互关联、相互促进的，渗透数学文化教育是发展数学核心素养的途径.因此，在数学教学中应该以数学文化作为抓手，把数学文化渗透在课堂中，挖掘背后的思想与思维品质，提升学生的数学素养.但我们大部分一线教师在教学中对数学文化的重视程度不够，担心在课堂中融入数学文化会影响教学进度，更关键的是缺乏对数学文化应有的认识，并且缺少相关的素养.而“两角差的余弦公式”一课就蕴含了丰富的数学文化，如何在教学中进行渗透呢？

4.1 展现数学知识形成的文化背景

三角学起源于天文学中的测量问题，两角差的余弦公式被称为平面三角学的基本公式之一，伴随着三角学的诞生而诞生，有关的历史素材丰富多彩.教师可向学生梳理两角差余弦公式的产生与发展过程，了解数学家托勒密、麦克肖恩、帕普斯与威塞尔等为公式证明所作的贡献，让学生感受到“方法之美”.

4．2 在问题情境创设中渗透数学文化

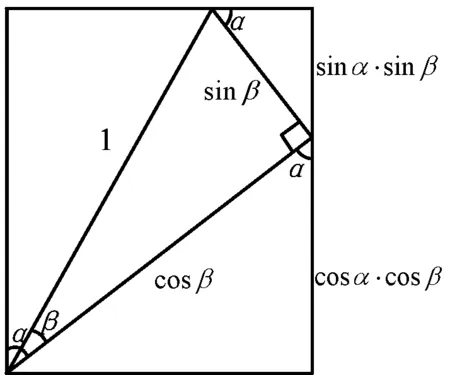
图2

著名的数学家黎曼有一句名言：每个数学公式背后，都有一个反映其本质的几何模型.我们可以创设这样的情境来引导学生猜想cos(α-β)的展开式：图2是来自我国一位数学爱好者编写的《无字证明集锦》，你有何发现？

本图是由学生熟悉的矩形和直角三角形构成，能清晰直观地展示出公式cos(α-β)=cosαcosβ+sinαsinβ，有助于学生直观想象素养的发展，激发学生学习的兴趣.

4．3 在公式推导中感受数学文化

要追求公式证明方法的多元化，既要尊重教材提供的证明方法，又要引导学生探索其他证明方法.通过一题多证来拓展学生的数学思维，提升学生的数学素养，下面展示几种方法:

方法1 1941年，美国数学家麦克肖恩应用三角形全等以及两点间的距离公式进行推导.如图3所示，易得△DOA≌△BOC,由|AD|=|BC|,得

cos(α-β)=cosαcosβ+sinαsinβ.

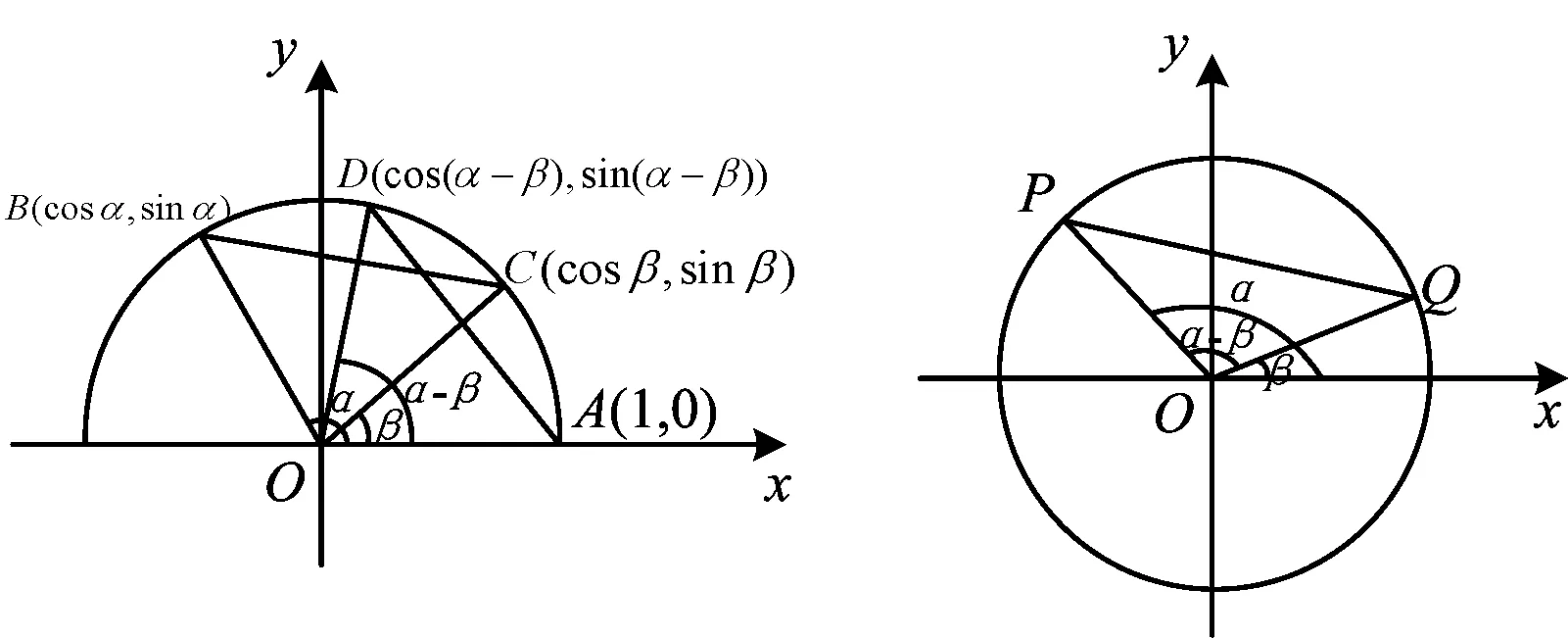
图3 图4

方法2 应用余弦定理推导.如图4，设P(cosα,sinα)，Q(cosβ,sinβ),则

|PQ|2=(cosα-cosβ)2+(sinα-sinβ)2=

2-2(cosαcosβ+sinαsinβ).

在△POQ中，

|PQ|2=|OQ|2+|OP|2-2|OQ||OP|cos(α-β)=

2-2cos(α-β),

从而

cos(α-β)=cosαcosβ+sinαsinβ.

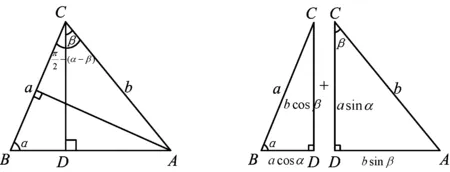
图5

方法3 利用三角形面积公式推导.上世纪80年代，我国中科院院士张景中先生有感于学生学习平面几何的困难，萌生了对传统平面几何教材加以改造的念头，以便让学生学得容易些.他敏锐地观察到可以使用面积法，将通常只作为一种特殊解题技巧的面积法扩展成一般方法，成为学生解几何题的一把快刀.如图5，由S△ABC=S△ABD+S△ADC，得

化简得 cos(α-β)=cosαcosβ+sinαsinβ.

总之，不管是哪种方法，其背后都有不同的巧妙构思.教师让学生体会各种证法的特色，体验美的享受，从而揭示数学家追求真善美的人文精神，这有助于培养学生的发散性思维与数学推理能力.

4．4 在公式运用中感悟数学文化

公式是一种新的运算，对于新的运算不仅要正用，还要逆用、变用，增强运算的灵活性与多向性，将数学文化与数学思想方法相结合，发展学生的数学运算素养与逻辑推理素养.

4.4.1 公式的正用

它不仅是公式的直接运用，关键是让学生体会这些诱导公式都是两角差余弦公式的特例，体现一般到特殊的思想.

4.4.2 公式的逆用

练习2 1)求：cos 13°cos 47°+cos 43°sin 167°;

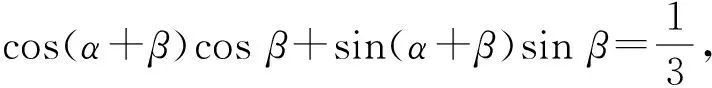
很多学生受思维定式的影响，对公式的逆用少之又少.教师要引导学生反思公式的结构特点，养成主动对公式进行逆用的意识，培养学生的逆向思维.

4.4.3 公式的变用

通过这道题可让学生深刻理解配角法的本质与优势，体会代换引起的三角函数形式的变化，从而有助于学生熟练、灵活地驾驭公式，对培养学生的转化化归思想及整体意识非常有益.

文化的传播和发展需要积累与沉淀，除了要重视课堂上的渗透外，还要重视课后的延续.像高斯函数、阿波罗尼斯圆、角谷猜想等出现在教材习题中，祖暅原理、刘徽割圆术、斐波那契数列等出现在教材“阅读与思考”栏目中，我们可引导学生课后借助网络对这部分内容进行深入了解.同时要利用好以数学文化为背景的高考试题与模拟题，有的数学文化试题以著名图形为背景，如赵爽弦图、杨辉三角等，有的出自我国经典古名著，像《九章算术》《算法统综》《数书九章》等，有的则出自数学名题，像勃罗卡点、将军饮马问题、米勒问题、皮克定理等.教师可通过让学生做这类题，加深对数学文化知识的理解.

李善良博士说：“要让学生欣赏、体验数学文化成为一种时尚，成为一种常态.”我们要把文化理念包含在教学活动中，发挥数学文化的作用，让学生感受到数学的魅力，让他们主动学习数学知识，从而真正提升学生的数学素养.