关注数学算法 创作数学命题*——以一个不等式问题证明为例

●余继光 ●张新志

(柯桥中学,浙江 绍兴 312030)(姜堰第二中学,江苏 泰州 225500)

算法是指解题方案的准确而完整的描述，是一系列解决问题的清晰指令.算法代表着用系统的方法描述解决问题的策略机制.进入人工智能时代，数学起着关键性作用，而人工智能的本质之一就是算法的升级与算法思想的研究，人工智能的发展对数学教学研究具有促进作用[1]．从算法的视角看数学命题创作值得思考，建立在数学基础知识、基本能力、基本思想之上的算法值得基础数学教学研究者关注，现以一个不等式问题的证明入手来审视算法的作用与影响．

1 一个不等式证明的算法启示

预备不等式：当x>0时，

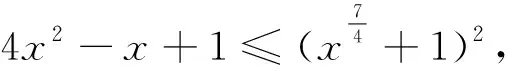
(1)

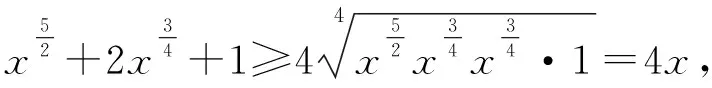
(2)

于是问题1转化为证明：

(3)

事实上，由基本不等式(a+b)(ab+1)≥b(a+1)2，即

评注 由式(1)到式(2)是一个结构一致、思维跳跃的智慧点，因为它们在条件abcd=1下是一致的，从而使不等式的结构隐藏得更深．

2 关注数学命题算法的意义

数学命题算法有三层意义：一是破解，二是更新，三是创新.在具体实践中，这三层意义是递进的.这一过程在命题实践中是经常采用的，比如在各地高考数学模拟测试中，很多命题并不是原创的，而是根据现有的某个命题进行改编的，其中一个途径就是在算法上进行变通[2]．

2.1 算法破解

首先，式(1)来自何处？引入待定系数k，使得4x2-x+1≤(xk+1)2成立，展开得x2k-1+2xk-1+1≥4x.如何让这一不等式恒成立呢？注意到左式的系数和为1+2+1=4恰好等于右式的系数，于是自然而然地就可以联想到利用四元均值不等式使得该不等式恒成立，从而得到待定系数k.由

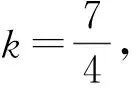
1.2 算法更新

其次，能否更新一种算法，命制一个新的数学问题呢？更新建立在已经具备的数学算法知识，比如利用向量数量积的运算性质的算法构造一个较容易证明的不等式．

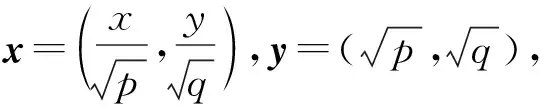
令x=2a+b，y=c+2d，p=a+b，q=c+d，即可证明原不等式．

1.3 算法创新

再次，能否创新一种算法，命制一个新的数学问题呢？创新需要灵感，灵感来自于长期创作实践的基础，构造思想是数学命题的创新之源．

证明 由ax+by+cz+dw=1，构造表达式λ(ax+by+cz+dw-1)=0(其中λ为实常数)，则

ax2+by2+cz2+dw2=ax2+by2+cz2+dw2+λ(ax+by+cz+dw-1)=

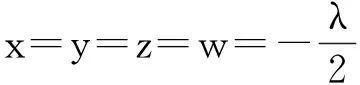
此证明的算法本质是构造思想.而构造思想也是创新思想的基础，此问题的呈现形式也可以是“正数a，b，c，d满足ax+by+cz+dw=1，则ax2+by2+cz2+dw2的最小值是______”，并期待其在高考数学命题中出现．

基础数学教学中的问题研究，寻找一般模型最重要.在由特殊到一般的探寻过程中，算法思想可以是不变的，抽象表达是关键，理解算法思想的内涵是根本．

3 变式体验算法内涵

证明 引入待定系数k，使得5x2-2x+1≤(xk+1)2成立，从而

x2k-1+2xk-1+2≥5x,

令4k-3=5，得k=2，从而5x2-2x+1≤(x2+1)2,利用式(3)即可得证．

证明 引入待定系数k，使得6x2-3x+1≤(xk+1)2成立,从而

x2k-1+2xk-1+3≥6x,

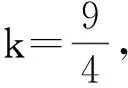
3.1 一般模型

问题7 设a，b，c，d>0，abcd=1，n∈N+，求证：

证明 引入待定系数k，使得(n+3)x2-nx+1≤(xk+1)2成立，从而

x2k-1+2xk-1+n≥(n+3)x,

由(n+3)元均值不等式可得

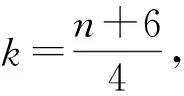
3.2 引伸变通

证明 tanα1tanα2=tanα3tanα4等价于tanα1tanα2cotα3cotα4=1,所证不等式等价于

令tanα1=a,tanα2=b,cotα3=c,cotα4=d，则原命题转化为问题5(下略)．

数学命题的核心之一是算法，人工智能的核心也是算法.根据《普通高中数学课程标准(2017年版)》的学业质量评价水平，“能够在综合的情境中，发现其中蕴含的数学关系，用数学的眼光找到合适的研究对象，用恰当的数学语言予以表达，并运用数学思维进行分析，提出数学问题”，此命题在此背景下创作而成，问题结构简洁、整齐，数学语言表达美；问题结构隐藏深，挖掘深，数学模型美；求解过程转化思想灵，拓展宽，将三角函数与代数结构有机结合，算法严谨，深化了求解人的数学思维层次，此问题对优秀学生的数学思维也是一次挑战[3]．