数学高考中的核心素养分析及反思*

●林 荣

(温州第二高级中学,浙江 温州 325007)

1 问题的提出

党的十九大提出“教育立德树人的根本任务，全面发展素质教育，培育学科核心素养”的目标[1].数学作为一门重要的学科，在培养学生核心素养方面有着举足轻重的作用.数学核心素养是具有数学基本特征的思维品质、关键能力以及情感、态度与价值观的综合表现，是在数学学习和应用的过程中逐步形成和发展的.新修订的《普通高中数学课程标准(2017年版)》(以下简称《新课标》)明确提出了数学学科核心素养包括：数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据分析.与实验版相比，容易发现在提出核心素养的前提下，《新课标》尤其强调了学业质量和考试评价的重要性，在内容上专门增加了“学业质量”的内容，这章内容主要就是描述如何评价核心素养，并在附录中提出了每个核心素养的3个评价水平.这说明《新课标》的制定者充分注意到了测试评价在落实核心素养培养过程中的重要性.要想落实核心素养的培养，就要先解决如何评价核心素养的问题，归根到底就是核心素养怎么考的问题.李尚志老师在《数学通报》2018年连续5期发表了系列文章“核心素养怎么考(一)～(五)”，以大学自主招生试题为引子给出了测试评价核心素养的具体实例，给了我们很多启发.从中可以看出对核心素养的测试评价需要教师的精心设计，不仅要有意识地命制测试评价核心素养的试题，而且还要在试题的形式上有所创新，甚至在试题的顺序编排上都要有所设计.作为高中生学业水平的终结性评价，也是高等院校选拔人才的重要途径，高考需要把学生核心素养发展的水平作为重要的评价内容纳入到测试评价之中.因此，从核心素养的角度重新审视现有的高考试题、研究现有高考试题中对核心素养的评价状况以及在此调查的基础上思考“如何测试评价核心素养”将是一项有益的工作.

2 核心素养视角下的高考数学试卷

以2016—2018年浙江省数学高考试卷为对象，分析试卷对核心素养的评价状况.数学核心素养的评价属于数学学习评价的范畴，《新课标》将每一个数学学科核心素养划分为3个水平，每个水平都通过数学学科核心素养的具体表现和体现数学学科核心素养的4个方面进行表述，这4个方面包括：情境与问题、知识与技能、思维与表达、交流与反思.而划分的3个水平分别对应高中学生3种不同的层次水平，即高中毕业水平、高考水平、拓展水平.文献[2]分析了《新课标》中的评价模型，结合了布鲁姆模型、PISA模型、SOLO模型等成熟的学习评价模型，提出了数学核心素养的生成源于知识的理论，由此提出把数学的核心素养水平划分为“知识理解”“知识迁移”“知识创新”，明确了3个水平划分的标准，具有可操作性.这里我们采用喻平老师提出的数学核心素养评价框架，把6个核心素养都划分为3个水平，如表1，对研究对象进行分析.

表1 学科核心素养评价框架

把核心素养与知识的获取及应用结合起来是比较合理的做法，因为学生核心素养的生成离不开知识的学习，而对核心素养的评价离不开对学生所学知识的考查.这种结合可以把核心素养落实到实处，使核心素养的考查成为有本之木、有源之水.为使每一个水平的划分标准更明确，喻平老师还对各级水平的具体表现进行了描述.

知识理解作为学习者学科核心素养的一级水平，具体表现为：1)了解知识产生的缘由；2)理解知识形成的结果；3)解决数学的基本问题.

知识迁移作为学习者学科核心素养的二级水平，具体表现为：1)有基本的类比推理能力，能够将知识迁移到不同情境中去，解决与数学知识相关的现实情境问题、数学内部不同情境问题、不同学科情境问题；2)能够理解知识之间的逻辑关系，掌握知识结构，掌握与知识相关的数学思想方法，能够判断知识迁移的准确性和有效性；3)能够解决需要多种知识介入、多种方法运用的常规性复杂问题.

知识创新作为学习者学科核心素养的三级水平，具体表现为：1)具有探究问题的意识；2)具备探究问题的能力；3)具备解决非常规数学问题的能力，能够灵活运用知识和方法解决非常规性问题；4)形成数学思维.

根据该评价框架，笔者对2016—2018年浙江省数学高考试卷的全部试题进行了分析，举例如下：

( )

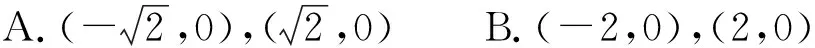
(2018年浙江省数学高考试题第2题)

该题考查双曲线焦点的概念，属于直接回忆概念就可以解决的，分值为4分，因此标定为A1-4.

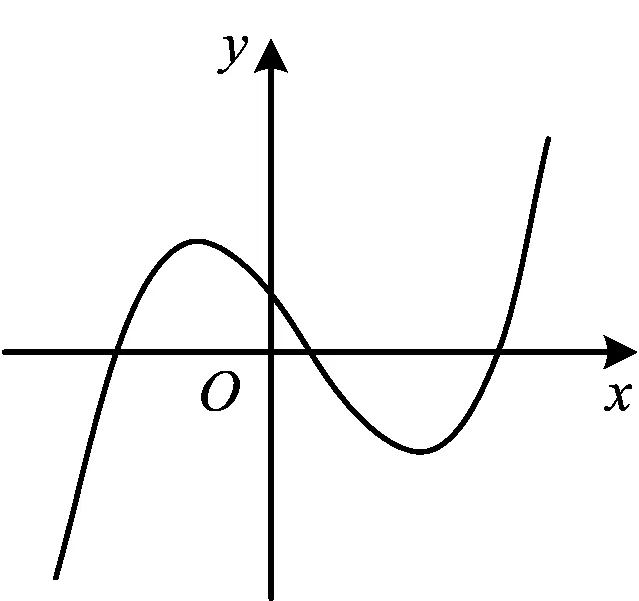
图1

例2 函数y=f(x)的导函数y=f′(x)的图像如图1所示，则函数y=f(x)的图像可能是

( )

A. B. C. D.

(2017年浙江省数学高考理科试题第7题)

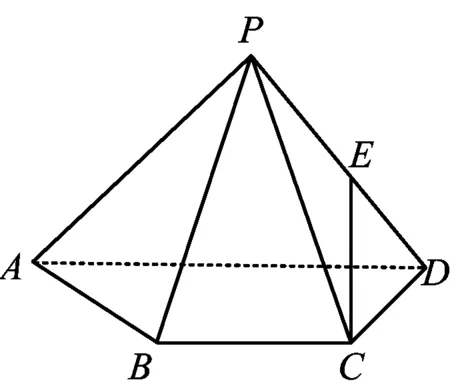
图2

该题考查学生图形的直观想象能力，需要学生在掌握知识的前提下有一定的逻辑思考能力，分值为4分，因此标定为I2-4.

例3 如图2，已知四棱锥P-ABCD，△PAD是以AD为斜边的等腰直角三角形，BC∥AD，CD⊥AD，PC=AD=2DC=2CB，E为PD的中点．

1)证明：CE∥平面PAB；

2)求直线CE与平面PBC所成角的正弦值．

(2017年浙江省数学高考理科试题第19题)

该题的第1)小题需要学生利用空间直线与平面的位置关系的判定和性质来证明线面平行的问题，主要是考查学生的逻辑推理能力，标定为R2-5.第2)小题涉及到空间的线面角的计算，考查学生对立体图形的直观想象以及空间几何量的计算，重点在于图形的直观想象，因此标定为I3-6，C2-4.

图3

1)求直线y=kx+1被椭圆截得的线段长(用a,k表示)；

2)若任意以点A(0,1)为圆心的圆与椭圆至多有3个公共点，求椭圆离心率的取值范围．

(2016年浙江省数学高考理科试题第19题)

以上对核心素养的标定方法参考了朱先东、吴增生老师在文献[3]中的标定方法，而文献[3]主要分析了中考试题，高考试题要比中考试题更加综合、更加复杂，因此在标定过程中有一些与中考题不同的情况，主要表现在高考试题考查得比较综合，有的题目往往不止考查单一的核心素养，尤其是解答题.遇到这种情况，若是客观题则采用重点考查的素养进行标定，若是解答题则以考查核心素养的比重进行标定.核心素养标定的分数以题目的卷面分数为主要依据，但不等同于试卷的评卷分数.因为高考评卷需要考虑的因素比较复杂，评卷分数不能反映试题考查核心素养的比重，所以最终在该题目总分不变的情况下，根据考查核心素养的比重标定分数(比如例3和例4).按照以上方法，笔者对2016—2018年浙江省数学高考试卷进行统计，得到试卷中不同的核心素养不同水平的权重，如表2所示：

表2 试卷中不同的核心素养不同水平的权重 %

年份素养水平C1C2C3CI1I2I3ID1D2D3D20165.3316.6716.0038.007.339.333.3320.000.000.000.000.00201710.6718.679.3338.675.334.6710.6720.670.002.670.002.6720185.3317.3316.6739.336.676.002.6715.330.002.670.002.67平均7.1117.5614.0038.676.446.675.5618.670.001.780.001.78

从表中数据可以看出数学抽象的权重为18.89%，逻辑推理的权重为18.67%，数学建模的权重为3.33%，数学运算的权重为38.67%，直观想象的权重为18.67%，数据分析的权重为1.78%.从整体上看，浙江省的高考试题在考查学生核心素养方面还是比较全面的，重点考查了学生的数学运算、数学抽象、逻辑推理、直观想象等核心素养.其中数学建模和数据分析的权重偏低是与浙江省考试内容的要求有关系的，因为统计内容不做解答题要求，另外浙江省一直注重考查数学的本质，很少考查应用题，所以在这两项核心素养的考查上明显偏低.这种测试评价实际上也会直接反馈到日常的教学之中，比如在高三复习过程中就经常会有教师纠结：函数模型的应用、三角函数模型的应用、解三角形的应用等等内容要不要复习？而现实中确实存在考试不考教师就不教的情况，尤其是在课时紧张的情况之下.另外从统计结果可以看出，数学运算的权重偏高，笔者认为这是正常现象，实际上高中数学比初中数学在运算能力要求上有所提高，不仅运算的复杂程度提高，对运算方法和思想都提出了更高的要求，而实际上运算能力的差别也是高中生数学学习能力差别的主要原因.另外高中的数学运算素养中也蕴涵着数学抽象、逻辑推理、直观想象这些核心素养，它是学生综合素养的一种表现.

3 核心素养背景下数学试题命制的尝试

新一轮的课程改革围绕核心素养展开，对核心素养的测试评价将直接影响核心素养的落实.《新课标》的编制者史宁中、鲍建生等人多次在不同的场合中鼓励一线教师参与到核心素养的测试评价中来.一线教师结合自身的教学实践和长期解题命题的经验，在核心素养测试评价的探索中是大有所为的.

在核心素养背景下命制数学试题，题型应该更加创新，可以设计多选题、逻辑题、数据分析题、举例题、开放题等形式[4].比如，2018年北京市数学高考卷中就出现了举例题：

例5 能说明“若f(x)>f(0)对任意的x∈(0.2]都成立，则f(x)在[0,2]上是增函数”为假命题的一个函数是______．

(2018年北京市数学高考理科试题第13题)

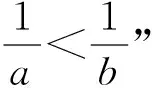
(2018年北京市数学高考文科试题第11题)

这种问题没有唯一的答案，让学生有更大的发挥空间，考查学生对概念的理解能力以及数学抽象能力和逻辑推理能力，能更有效地反映学生的核心素养水平.

在核心素养背景下命制试题，应考虑试题考查的主要核心素养有哪些、如何考查出学生不同水平的核心素养.问题设计可以更加开放一些，比如：

例7 一根直杆为什么能从弯曲的洞中通过？

一条直铁棍固定在一个可以旋转的Γ型支架上，并与Γ型支架的横臂垂直.Γ型支架的竖臂可以绕着桌面的一个定点O自由旋转，旋转过程中保持横臂与桌面平行，同时桌面上有一个与桌面垂直的且经过点O的平面α.当直铁棍与桌面不垂直的情况下，要使整个旋转过程中直铁棍能够无障碍地穿过平面α，则必须在平面α上挖一个怎样的洞？

试题说明 本题考查学生的直观想象、数学建模、逻辑推理、数学运算等核心素养.虽然看上去有点超纲，但是只要是学过立体几何、圆锥曲线和三角函数知识的学生都是有能力解决这个问题的，关键是怎么将这些知识综合运用起来，而对知识的创造性应用正是核心素养三级水平的要求.

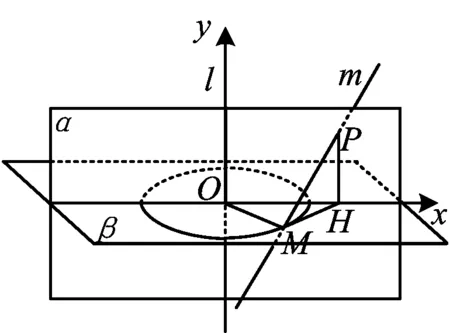
图4

解 如图4所示，动直线m绕定直线l旋转，直线m与直线l所成的角为定值φ0，它们之间的距离为定值a，设经过直线l的竖直平面为α，直线m∩α=P，求点P的轨迹.

下面给出证明：过点O作OM⊥直线m于点M，OM⊥直线l于点O，则OM=a，即点M在以O为圆心、半径为a的圆上运动.设这个圆所在的平面为β，以平面α与平面β的交线为x轴、直线l为y轴建立直角坐标系.设P(x,y)，记∠MOx=θ，过点P作PH⊥x轴于点H，则PH⊥β，又OM⊥MP，得OM⊥MH，从而

又由PH∥l，得∠MPH=φ0，从而

于是

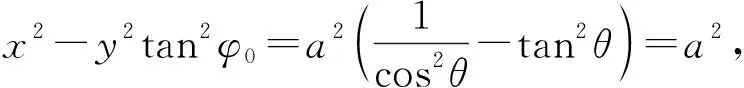
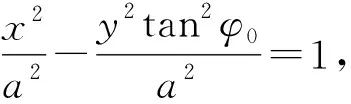
故点P的轨迹是双曲线.

素养分析 本试题在考查学生核心素养方面有不同的表现形式，如果只考查较低水平的核心素养，那么可以设计为选择题.另外，不同水平的核心素养在本题中都有所体现(如表3)：

表3 不同水平的核心素养在例7中的体现

核心素养背景下的高中数学测评实践研究是一个不断探索的过程，它必须建立在原有测评手段的基础之上.浙江省数学高考命题水平是有目共睹的，其对数学本质的考查，体现了数学最深刻的魅力，这些试题在任何时候都不会过时.核心素养的提出对数学测评也提出了新的要求，数学试卷中适当地增加一些文字描述，多一些现实背景，也是数学测评的一个趋势.教师应把握新的机会，在数学核心素养的测评研究中大显身手.