Common Fixed Points for Two Mappings with Implicit-linear Contractions on Partially Ordered 2-metric Spaces
Piao Yong-jie
(Department of Mathematics,College of Science,Yanbian University,Yanji,Jilin,133002)
Communicated by Ji You-qing
Abstract: In this paper,we introduce a new class U of 3-dimensional real functions,use U and a 2-dimensional real function ϕ to construct a new implicit-linear contractive condition and obtain some existence theorems of common fixed points for two mappings on partially ordered 2-metric spaces and give a sufficient condition under which there exists a unique common fixed point.The obtained results goodly generalize and improve the corresponding conclusions in references.
Key words: 2-metric space,class U of functions,implicit-linear contraction,common fixed point
1 Introduction and Preliminaries
The following definition can be found in[1].
Definition 1.1Letbe a partially ordered 2-metric space,S,T:X →X two maps.S,T are said to be weakly C∗-contractive maps if there exists a continuous function0 such that for any x,y,a ∈X with
d(Sx,Ty,a)≤kd(x,y,a)+l[d(x,Ty,a)+d(y,Sx,a)]−φ(d(x,Ty,a),d(y,Sx,a)),where k and l are two real numbers satisfying l>0 and 0 Piao[1]obtained the existence theorems of common fixed points for two weakly C∗-contractive mappings S and T under the continuous and non-continuous conditions and gave a sufficient condition under which there exists a unique common fixed point. The obtained results are not only the generalizations and improvements of the corresponding results in[2],but also the supplementary results of the corresponding results in[3]–[13]. In this paper,we introduce a class U of 3-dimensional real functions and define a new contractive condition by replacing the linear condition in Definition 1.1 with a implicit condition and discuss the existence problems of common fixed points for two mappings and give a sufficient condition under which there exists a unique common fixed point. Definition 1.2[3]A 2-metric space(X,d)consists of a nonempty set X and a function d:X×X×X →[0,+∞)such that (i) for distant elements x,y ∈X,there exists a u ∈X such that d(x,y,u)=0; (ii) d(x,y,z)=0 if and only if at least two elements in{x,y,z}are equal; (iii) d(x,y,z)=d(u,v,w),where{u,v,w}is any permutation of{x,y,z};( iv) d(x,y,z)≤d(x,y,u)+d(x,u,z)+d(u,y,z)for all x,y,z,u ∈X. Definition 1.3[3]A sequence xnnN in 2-metric space(X,d)is said to be a Cauchy sequence,if for each ε>0 there {exis}ts ∈a positive integer N N such that d(xn,xm,a)<ε for all a ∈X and n,m>N.A sequence{xn}n∈N is sai d∈ to be convergent to x ∈X,if for each a ∈X,n→lim+∞d(xn,x,a)=0.And we write that xn→x and call x the limit of{xn}n∈N.A 2-metric space(X,d)is said to be complete,if every Cauchy sequence in X is convergent. Definition 1.4[6]Let(X,d)be a 2-metric space,and a,b ∈X,r>0.The set is said to be a 2-ball with centers a and b and radius r.Each 2-metric d on X generalizes a topology τ on X whose base is the family of 2-balls.τ is said to be a 2-metric topology. Lemma 1.1[10]If a sequence xnnN in a 2-metric space(X,d)is convergent to x,then Lemma 1.2[13]Let{xn}n∈N be a sequence in(X,d)satisfying If{xn}is not Cauchy,then there exist a ∈X and ϵ>0 such that for any i ∈N,there exist m(i),n(i)∈N with m(i)>n(i)>i,d(xm(i),xn(i),a)>ϵ,but d(xm(i)−1,xn(i),a)≤ϵ. Lemma 1.3[6]in 2-metric space(X,d)if and only ifin 2-metric topology space X Lemma 1.4[6]Let X and Y be two 2-metric spaces and T:X →Y a map. If T is continuous,thenimplies Lemma 1.5[6]Each 2-metric space is T2-space. At first,we define two new classes of real functions as follows.∈U ⇐⇒ ∞ → ∞is a continuous and non-decreasing function satisfying the following two conditions: (U1)u ≤v whenever u ≤F(v,u+v,0)or u ≤F(v,0,u+v)for u,v ≥0; (U2)F(x,2x,0)≤x,F(x,0,2x)≤x,F(x,x,x)≤x for all x ≥0.is a function satisfying the following two conditions:for any two sequences Example 2.1Let where two non-negative real numbers k1,k2satisfy that k2>0 and 0 d(Sx,Ty,a)≤F1(d(x,y,a),d(x,Ty,a),d(y,Sx,a))−φ(d(x,Ty,a),d(y,Sx,a)). Example 2.2Let Obviously,F2is continuous and non-decreasing.If u,v ≥0 and u ≤F2(v,u+v,0),then we obtain u ≤u[1+2v+u]≤v. Similarly,if u,v 0 and uF2(v,0,u+v),then uv.Hence(1)holds.If x0,then Hence(U2)holds.Therefore F2∈U. Example 2.3Let ϕ1(x,y)=x2+y2, ϕ2(x,y)=max{x,y}, x,y ≥0. Then ϕ1,ϕ2∈Φ.Since ϕ1and ϕ2are continuous,they are both φ in Definition 1.1. Example 2.4Let ϕ3(x,y):[0,+∞)×[0,+∞)→[0,+∞)be defined by ϕ3(x,y)=0 if and only if(x,y)=(0,0)and ϕ3(x,y)=x+y+1 for all(x,y)/=(0,0).Then,obviously,ϕ3∈Φ,but ϕ3is not φ in Definitions 1.1 since ϕ3is not continuous at(0,0). Theorem 2.1Let(X,d)be a 2-metric space and S,T:X →X two mappings.Suppose that for each x,y,a ∈X, d(Sx,Ty,a)≤F(d(x,y,a),d(x,Ty,a),d(y,Sx,a))−ϕ(d(x,y,a),d(Sx,Ty,a)),(2.1)where F ∈U,ϕ ∈Φ.If S(X)or T(X)is complete,then S and T have a unique common fixed point. Proof. Take any x0X and construct a sequencexnas follows Hence By using(2.3),Definition 1.2(iv)and the non-decreasing property of F,we obtain from(2.2)that Hence,by(U1),one has Similarly,for each n=0,1,2,···and a ∈X,by(2.1),we have Let a=x2n+1in(2.5).Then we also obtain and d(x2n+3,x2n+2,a)≤F(d(x2n+2,x2n+1,a),0,d(x2n+1,x2n+2,a)+d(x2n+2,x2n+3,a)). Hence,by(U1)again,we have Combining(2.3),(2.4),(2.6)and(2.7),we have Let By using(2.1)we have Letting n →∞and using the properties of F and ϕ,we obtain from(2.9)that Hence ϕ(ξ(a),ξ(a))=0. Therefore,ξ(a)=0 by(ϕ2),i.e., Using(2.8)and following the proof of the main theorems in[1],we obtain the following result: If{xn}is not a Cauchy sequence,then by Lemma 1.2 and(2.10),there exists a b ∈X and an ϵ>0 such that for each natural number k,there exist two natural numbers m(k)and n(k)satisfying m(k)>n(k)>k and By using(2.11)and(2.12)we obtain the next result(for details,see the proofs of Theorems in[1]): We can assume that the parity of m(k)and n(k)is different by(2.10).Let m(k)be odd and n(k)be even.Then we have Letting k →∞in the above and using(2.13)and the properties of F and ϕ,we obtain≤ Hence so ϵ=0,which is a contradiction.Therefore,{xn}is a Cauchy sequence. Suppose that SX is complete.Since x2n+1=Sx2n∈SX for all n=0,1,2,···,there exists a u ∈SX such that x2n+1→u as n →∞.And{xn}is Cauchy and the following holds: H≤ence x2n+2u as n. By using L→emma 1. 1→,t∞he properties of F and ϕ and(2.1),we have that for each a X, Hence ϕ(0,d(u,Tu,a))=0. Therefore, d(u,Tu,a)=0 by(ϕ2)for all a ∈X,which implies that Tu=u. Similarly,we have Hence Su=u. This completes that Tu=Su=u, i.e.,u is a common fixed point of S and T. If v is another common fixed point of S and T,then u /=v.Hence there exists an a∗∈X such that d(u,v,a∗)>0. In view of(2.1),it is easy to see that Similarly,we can obtain the same conclusion for TX being complete. Next,we discuss the existence problems of common fixed points for two mappings on non-complete partially ordered 2-metric spaces. Theorem 2.2Let(X,d)be a partially ordered 2-metric space and S,T:X →X two mappings.Suppose that for each two comparable elements x,y ∈X and any a ∈X,(2.1)holds.If S and T satisfy the following conditions: (ii) S and T are continuous; (iii) S(X)or T(X)is complete, then S and T have a common fixed point. Proof. Taking any element x0∈X and using(i),we obtain Hence the s≤equence {xn}sat i≤sfies This shows that xnand xmare comparable for each m,Hence modifying the proof of Theorem 2.1,we can prove that{xn}is a Cauchy sequence and there exists a u ∈X such that xn→u as n →∞by(iii).Hence in view of(ii)and Lemma 1.4,we have That is to say that u is a common fixed point of S and T.The proof is completed. The following result is a new version of Theorem 2.2 under S and T being non-continuous. Theorem 2.3Let(X,d)be a partially ordered 2-metric space and S,T:X →X two mappings.Suppose that for each two comparable elements x,y ∈X and any a ∈X,(2.1)holds.If S and T satisfy the following conditions: (iii) S(X)or T(X)is complete, then S and T have a common fixed point. Proof. From the proof of Theorem 2.2 we know that there exists a non-decreasing sequencesatisfying(2.16)and xn→u as n →∞for some u ∈X by(i)and(iii). Hence xnu for all n by(ii).In view of(2.1),modifying the proof of Theorem 2.1,we also obtain(2.14)and(2.15).Hence ϕ(0,d(u,Tu,a))=ϕ(0,d(u,Su,a))=0, a ∈X. Therefore, Tu=Su=u, i.e.,u is a common fixed point of S and T.The proof is completed. Now,we give a sufficient condition under which there exists a unique common fixed point for two mappings in Theorems 2.2 and 2.3. Theorem 2.4Suppose that all of the conditions in Theorem 2.2 or Theorem 2.3 hold.Furthermore,if (I) for each x,y ∈X,there exists a z ∈X such that z and x are comparable,z and y are comparable; Case 1. u and v are comparable. In this case,by(2.1),we have Hence it is easy to obtain that d(u,v,a∗)=0 by the property of ϕ,this is a contradiction to the choice of a∗.Therefore,u is the unique common fixed point of S and T. Case 2. u and v are not comparable. By(I),there exists a w ∈X such that w and u are comparable and w and v are also comparable.Hence w /=u and w /=v.Assume that u ≺w.Then by(II)and the condition(i)in Theorem 2.2 or Theorem 2.3,we obtain that for each which means that Snu and Tnw are comparable.By(2.1),for each fixed a ∈X,we have If there exists a positive number n such that d(u,T n−1w,a) then,by the property of ϕ,we have ϕ(d(u,T n−1w,a),d(u,Tnw,a))>0. Hence,by the property of F,we obtain from(2.17)that≤ which is a contradiction.So This shows that for each fixed a ∈X,is a non-increasing and nonnegative real sequence.Hence there exists an M(a)0 such that Letting n →∞in(2.17)and using(2.18)and the properties of F and ϕ,we obtain M(a)≤F(M(a),M(a),M(a))−ϕ(M(a),M(a))≤M(a)−ϕ(M(a),M(a))≤M(a). Hence M(a)=0 by the property of ϕ again,i.e., Therefore, If u in the above derivation process is replaced by v,then we similarly obtain Hence u=v by Lemma 1.5,which is a contradiction.Therefore,u is the unique common fixed point of S and T. Remark 2.1In view of Examples 2.1–2.4 we know that(2.1)are very weaker than the contractive condition in Definition 1.1. Hence Theorems 2.1–2.4 greatly generalize and improve the results in[1]and others.
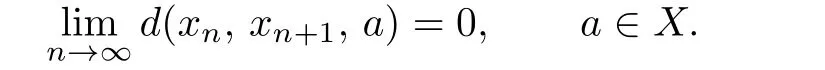
2 Unique Common Fixed Point
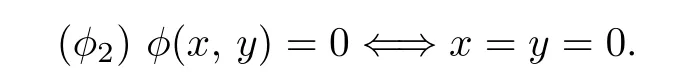
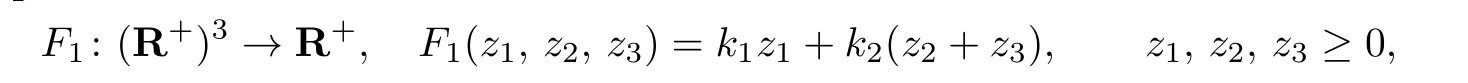




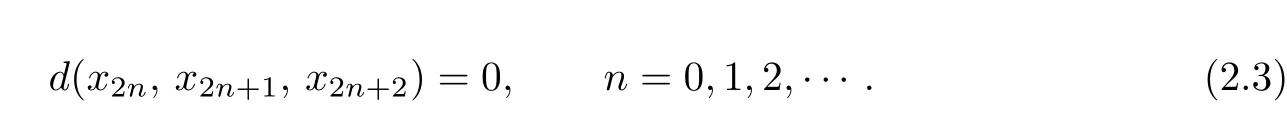




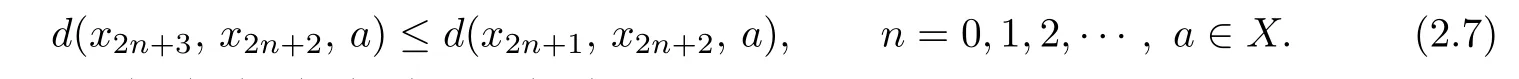




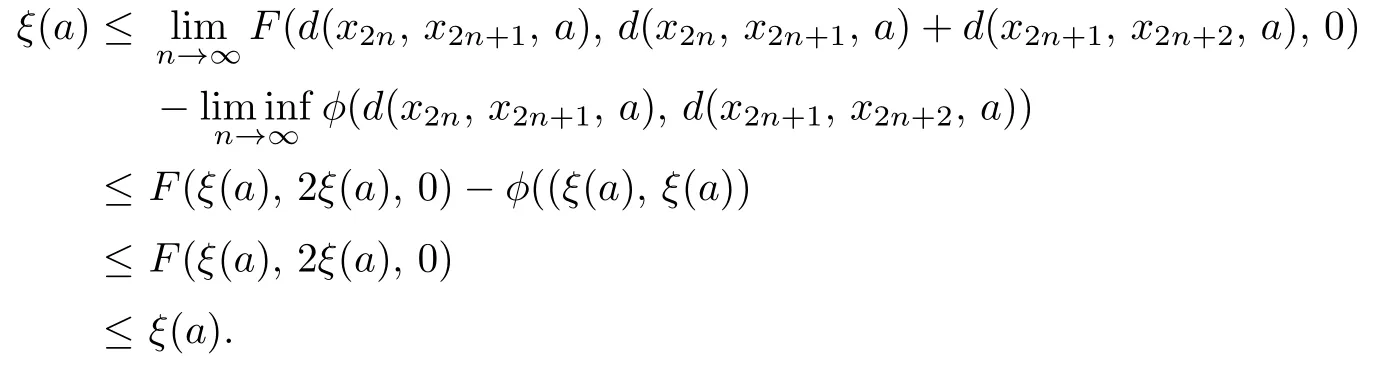


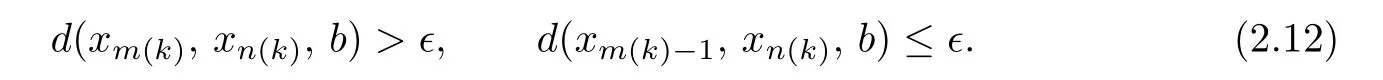
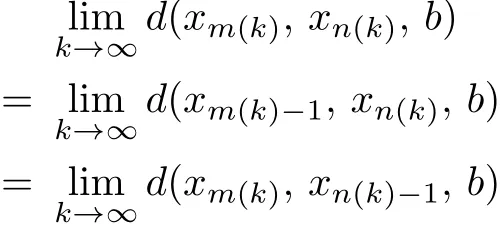


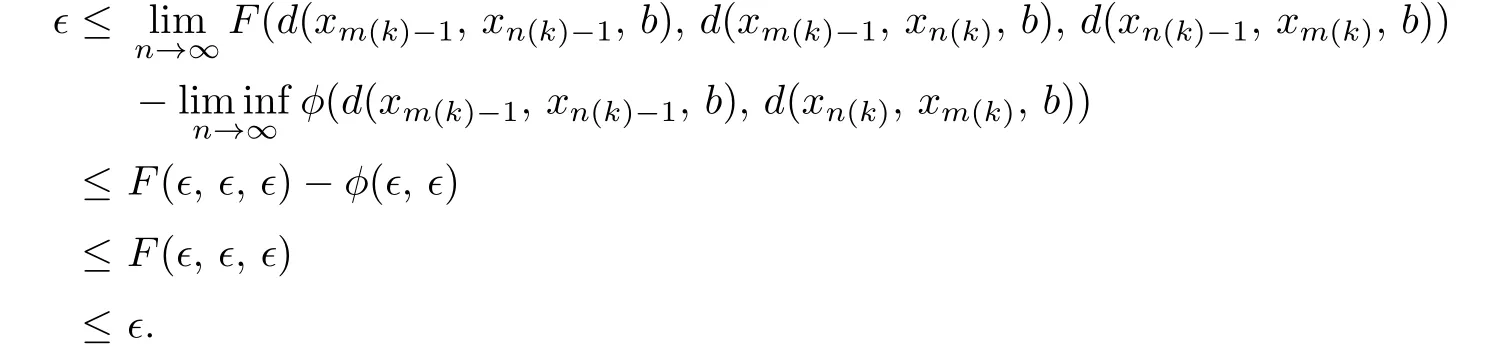
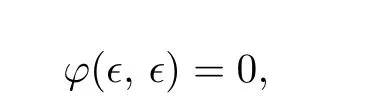


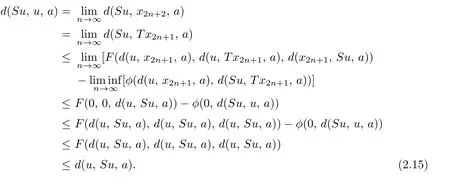
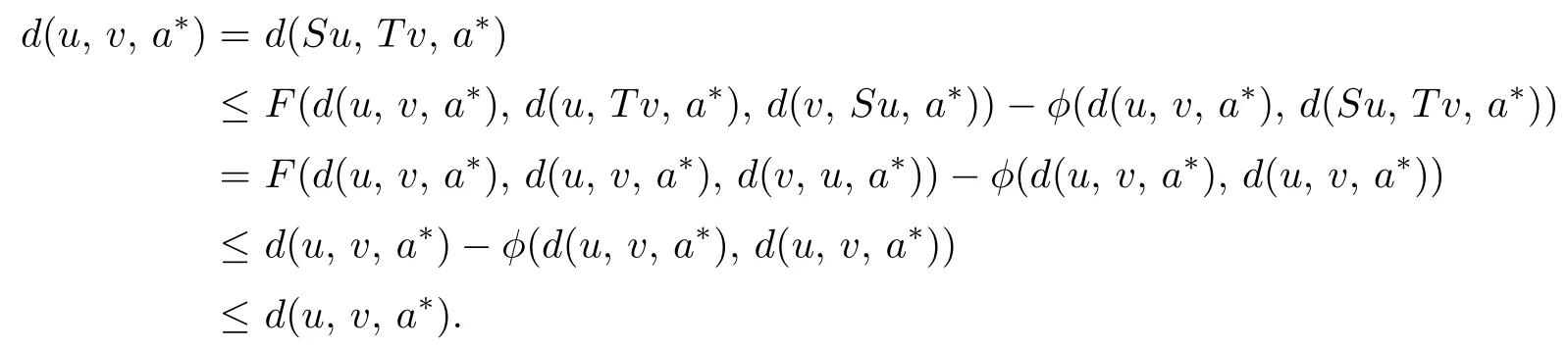







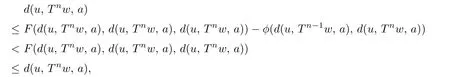


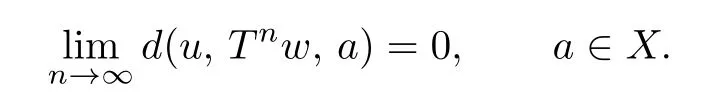


 Communications in Mathematical Research2019年3期
Communications in Mathematical Research2019年3期
