Fekete-SzegInequality for a Subclass of Bi-univalent Functions Associated with Hohlov Operator and Quasi-subordination
Guo Dong, Tang Huo, Ao En and Xiong Liang-peng
(1.Foundation Department,Chuzhou Vocational and Technical College,Chuzhou,Anhui,239000)
(2.School of Mathematics and Statistics,Chifeng University,Chifeng,Inner Mongolia,024000)
(3.School of Mathematics and Statistics,Wuhan University,Wuhan,430072)
Communicated by Ji You-qing
Abstract:In this paper,we introduce a new subclass of bi-univalent functions defined by quasi-subordination and Hohlov operator and obtain the coefficient estimates and Fekete-Szeg¨o inequality for function in this new subclass.The results presented in this paper improve or generalize the recent works of other authors.
Key words:analytic function,univalent function,bi-univalent function,coefficient estimate,Fekete-Szeg¨o inequality,Hohlov operator,quasi-subordination
1 Introduction
Let H denote the class of functions of the form

which are analytic in the open unit disk U={z:|z|<1}. Further,by S we denote the family of all functions in H which are univalent in U.
In[1],Robertson introduced the concept of quasi-subordination.For two analytic functions f and φ,the function f is quasi-subordination to φ written as
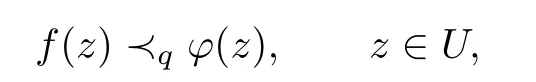
if there exist analytic functions h and ω with h(z)1,ω(0)=0 and|ω(z)|<1 such that
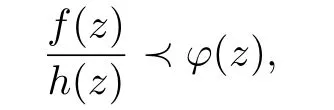
which is equivalent to

Observe that if h(z)≡1,then the quasi-subordination reduces to be subordination.Also,if ω(z)=z,then
f(z)=h(z)φ(z),
and in this case we say that f(z)is majorized by φ(z)and it is written as
f(z)≪φ(z), z ∈U.
Obviously,the quasi-subordination is the generalization of subordination as well as majorization.
For the functions f,g ∈H,where f(z)is given by(1.1)and
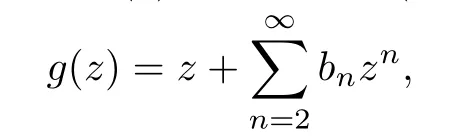
the Hadamard product or convolution is denoted by f ∗g and is defined by:
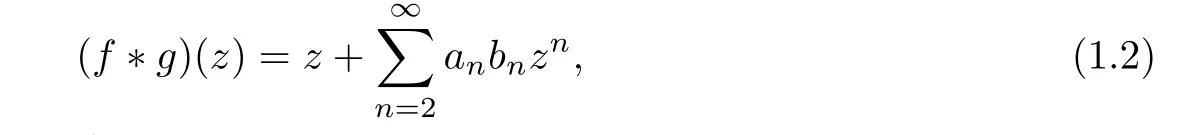
and the Gaussian hypergeometric function2F1(a,b,c;z)for the complex parameters a,b and c with cis defined by:
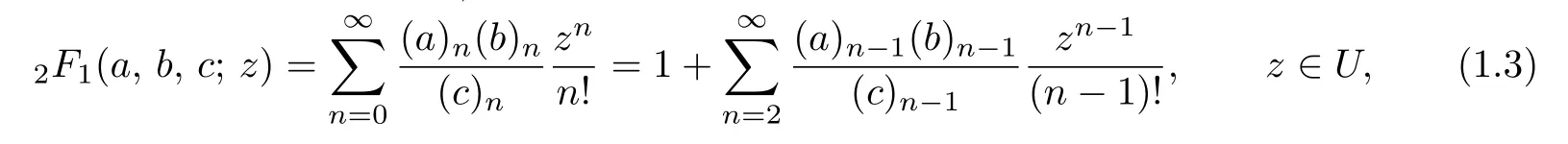
where(l)ndenotes the Pochhammer symbol(the shifted factorial)defined by:··· − ···
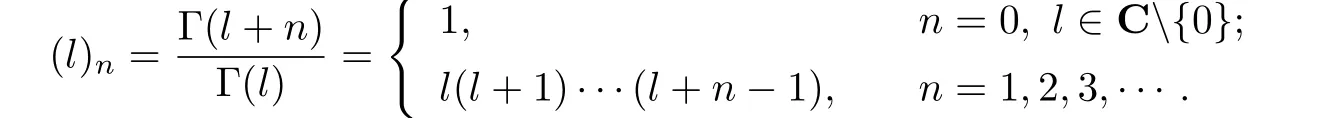
For the positive real values a,b and c(c /=0,−1,−2,−3,···),Hohlov[2]–[3]introduced a convolution operator Ia,b;cby using the Gaussian hypergeometric function2F1(a,b,c;z)given by(1.3)as follows:

where

Observe that,if b=1 in(1.5),then the Hohlov operator Ia,b;creduces to the Carlson-Shaffer operator.Also it can be easily seen that the Hohlov operator is a generalization of the Ruscheweyh derivative operator and the Bernardi-Libera-Livingston operator.
It is well known that every function f ∈S has an inverse f−1,which is defined by
f −1(f(z))=z, z ∈U
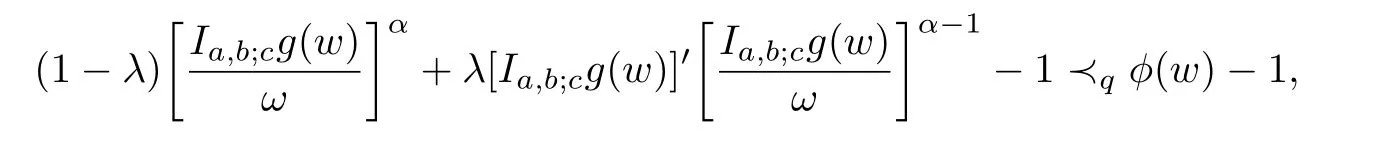
and
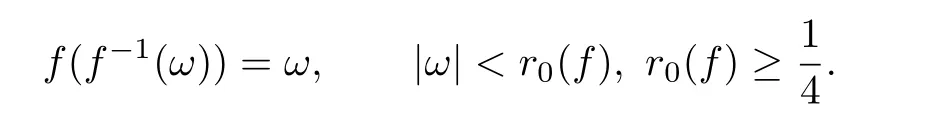
The inverse functions g=f−1is given by
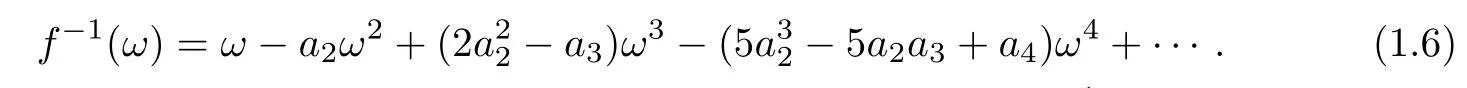
A function f ∈H is said to be bi-univalent in U if both f and f−1are univalent in U.Let Σ denote the class of all bi-univalent functions in U given by(1.1).
For functions in the class Σ,Lewin[4]proved that|a2|<1.51. Brannan and Clunie[5]improved Lewin’s results toand later Netanyahu[6]proved that maxif f(z)∈Σ.However,the coefficient estimates problem for each|an|(n=3,4,···)is still an open problem. Brannan and Taha[7](see also[8])introduced certain subclasses of the bi-univalent function class Σ such asthe class of strongly bi-starlike functions of order α and,the class of bi-starlike functions of order β.
Throughout this paper it is assumed that h(z)is analytic in U with h(z)1 and let
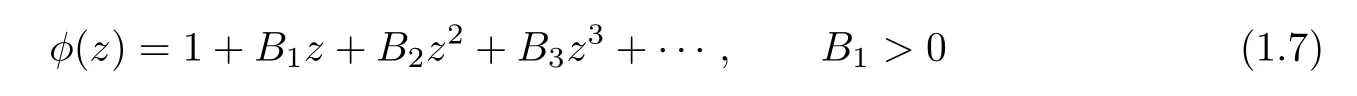
and
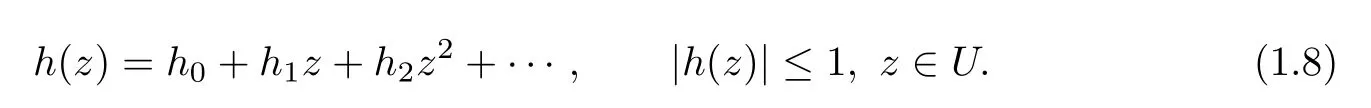
Using quasi-subordination and Hohlov operator,now we define the following classof analytic functions.
Definition 1.1A function f ∈Σ given by(1.1)is said to be in the classif it satisfies
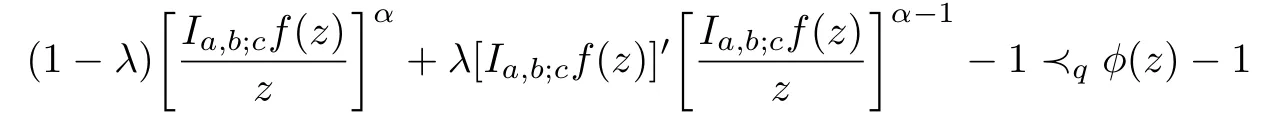
and
where α ≥0,λ ≥0,z,w ∈U and the functions g=f−1and ϕ are given by(1.6)and(1.7),respectively.
We note that
(1)For a=c and h(z)=b=1,the function class given by

was studied by Tang et al.[9](also see[10]).
(2)For a=c and h(z)=b=α=1,the function class given by
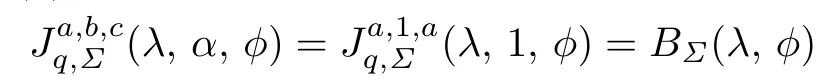
was studied by Peng and Han[11].
(3)For a=c,h(z)=b=α=λ=1,the function class given by
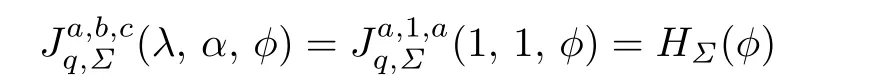
was studied by Guo et al.[12].
(4)For h(z)=λ=1,the function class given by
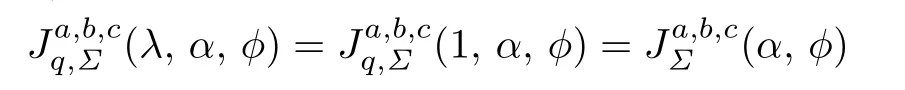
was studied by Pail and Naik[13].
(5)For a=c and b=α=1,the function class given by

was studied by Pail and Naik[14].
(6)For h(z)=λ=α=1,the function class given by

was studied by Omar et al.[15].
(7)For a=c and b=λ=1,the function class given by
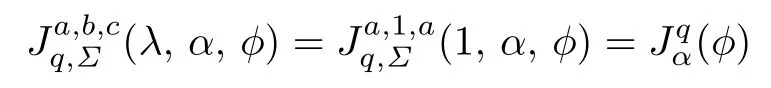
was studied by Goyal et al.[16].
(8)For a=c and b=λ=α=1,the function class given by
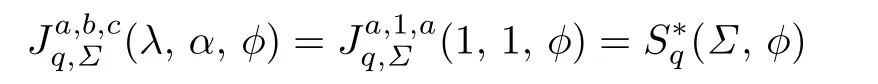
was studied by Algahtani[17].
In order to derive our main results,we need the following lemma.
Lemma 1.1[18]Let u(z)be an analytic function with u(0)=0,|u(z)|<1,and let··· ∈

Then|c1|≤1 and|cn|≤1 −|c1|2(n ≥2).
2 Coefficient Estimates
Theorem 2.1Let f(z)∈Σ given by(1.1)be in the class.Then

where
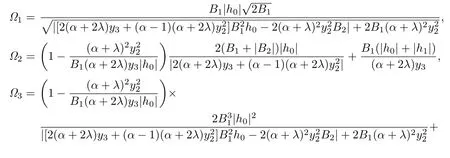
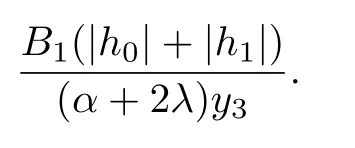
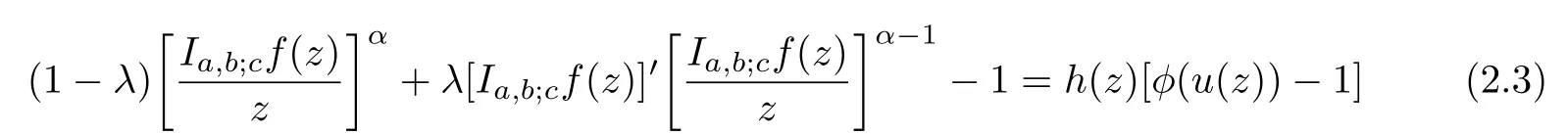
and

Define the functions u and v as
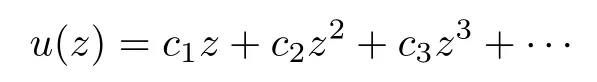
and···
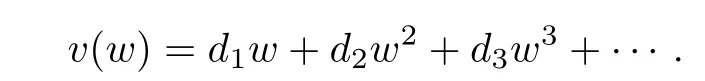
Thus,from(1.7)and(1.8),it follows that

and
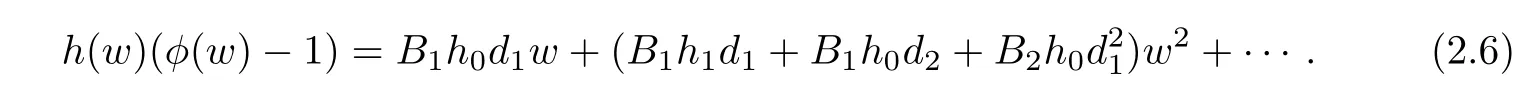
Now,by equating the coefficients in(2.3)and(2.4),we get
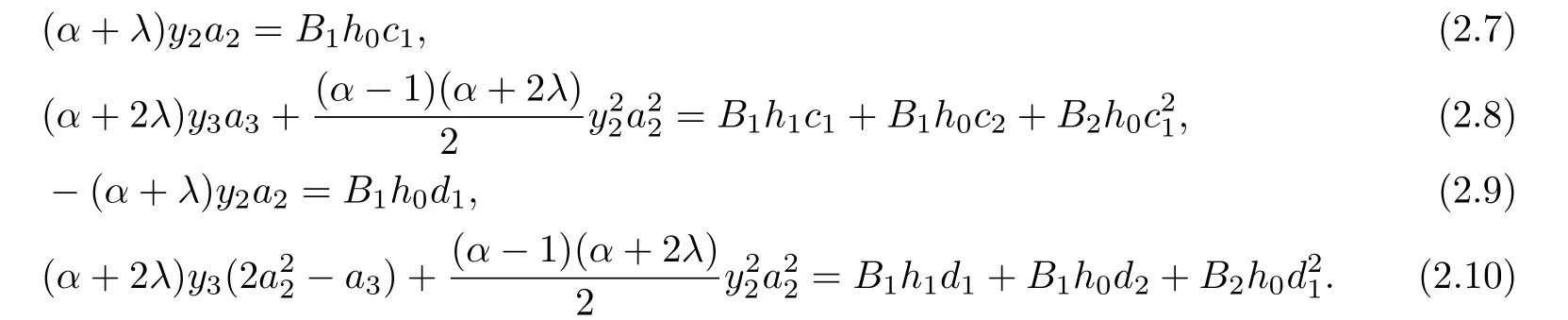
From(2.7)and(2.9),we get

and

Applying Lemma 1.1 for the coefficients c1and d1,we have

Adding(2.8)and(2.10)and by using(2.11),we get
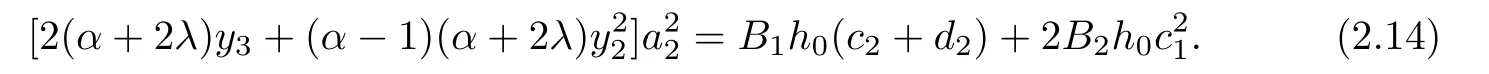
Applying Lemma 1.1 for the coefficients c2,d2and c1,we have
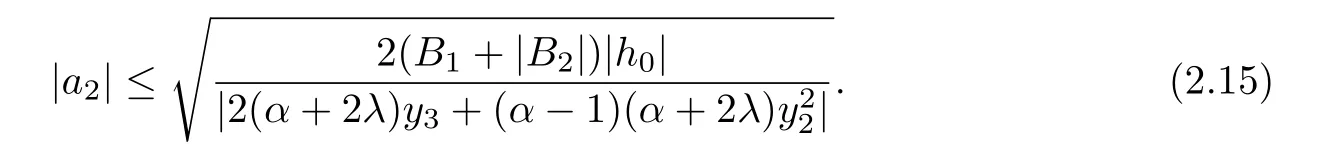
Substituting(2.11)and(2.12)into(2.14),we have

From(2.11),(2.12)and(2.16),we get
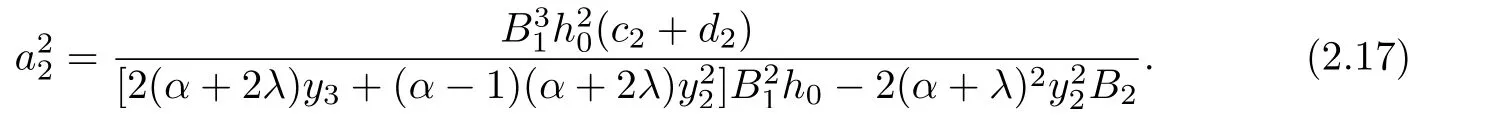
Using Lemma 1.1 and(2.7),we obtian
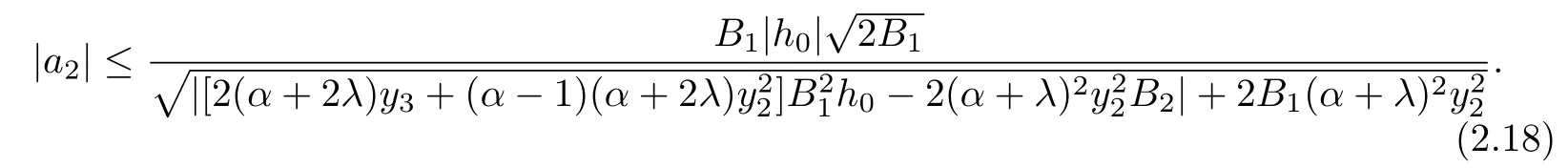
Next,in order to find the bound on a3,by subtracting(2.10)from(2.8),we get
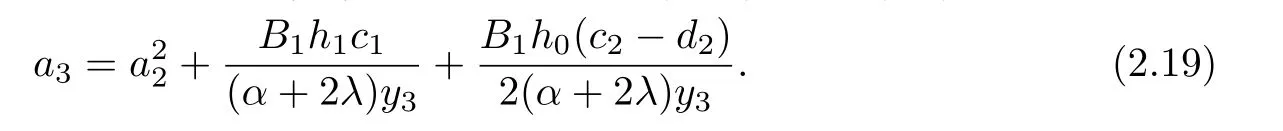
It follows from(2.7),(2.11),(2.19)and Lemma 1.1,we get
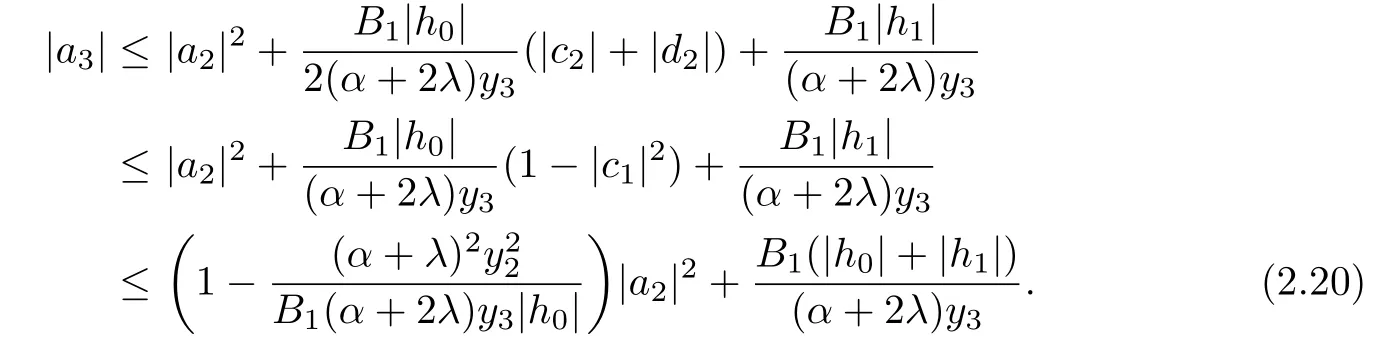
From(2.13),(2.15),(2.18)and(2.20),we have the assertion(2.2).This completes the proof of Theorem 2.1.
Theorem 2.2Let f(z)given by(1.1)be in the classand δ ∈R.Then
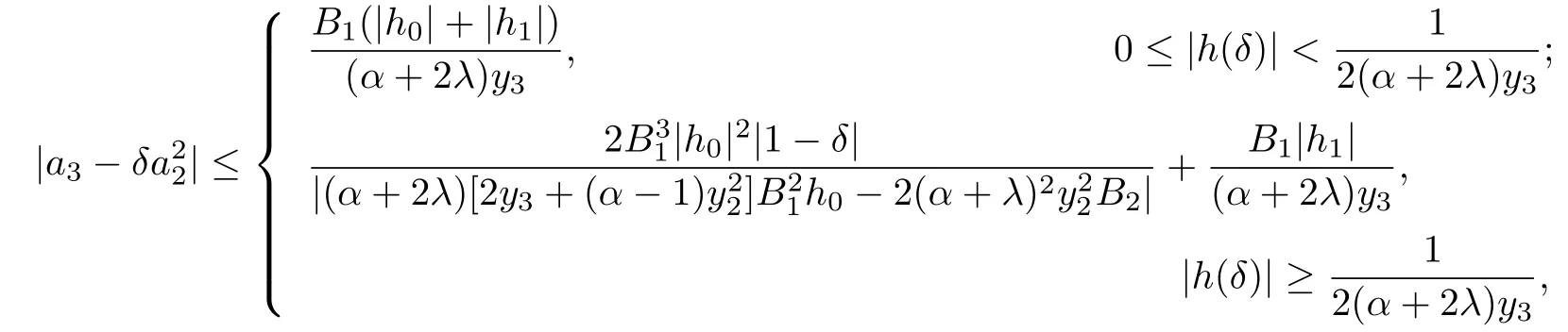
where
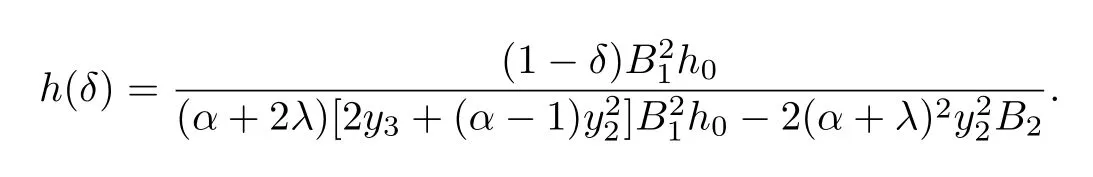
Proof. By using the equalities(2.17)and(2.19),we have
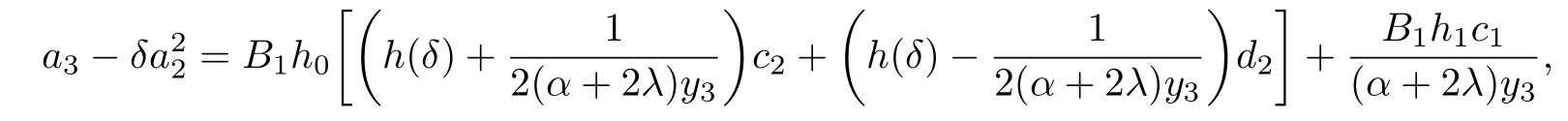
where

which completes the proof.
3 Corollaries and Consequences
Taking a=c and h(z)=b=1 in Theorem 2.1,we have the following corollary.
Corollary 3.1Let f(z)given by(1.1)be in the class.Then
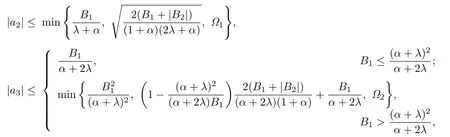
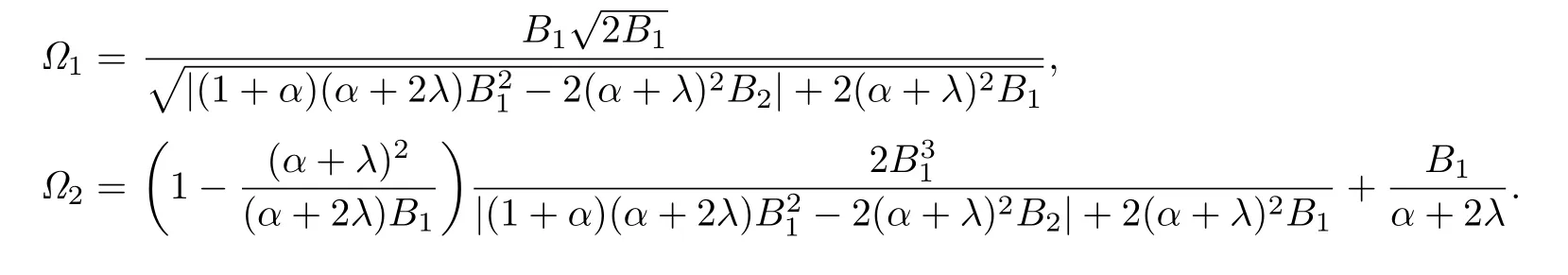
whereRemark 3.1The estimate of|a3|in Corollary 3.1 is the improvement of the estimate obtained in Theorem 2.1 of[9].
Setting a=c and h(z)=b=α=1 in Theorem 2.1,we have the following corollary.
Corollary 3.2Let f(z)given by(1.1)be in the class BΣ(λ,ϕ).Then

where
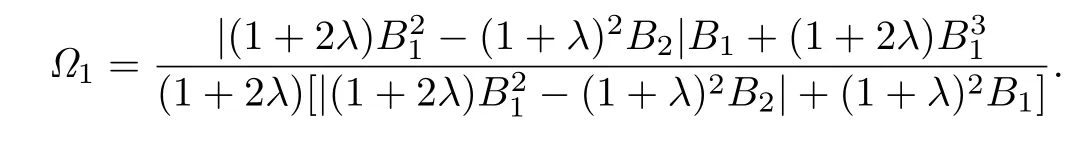
Remark 3.2The estimates for|a2|and|a3|asserted by Corollary 3.2 are more accurate than those given by Theorem 2.5 in[11].
Setting a=c,h(z)=b=α=λ=1 in Theorem 2.1,Theorem 2.1 reduces to the correspongding results of Guo et al.[12],which we recall here as Corollary 3.3.
Corollary 3.3Let f(z)given by(1.1)be in the class HΣ(ϕ).Then

Remark 3.3The estimates for|a2|and|a3|asserted by Corollary 3.3 are more accurate than those given by Theorem 2.1 in[11].
Setting h(z)=λ=1 in Theorem 2.1,we have the following corollary.
Corollary 3.4Let f(z)given by(1.1)be in the class(α,ϕ).Then

where

Remark 3.4The estimates for|a2|and|a3|asserted by Corollary 3.4 are more accurate than those given by Theorem 2.2 in[13].
Setting a=c and b=α=1 in Theorem 2.1,we have the following corollary.
Corollary 3.5Let f(z)given by(1.1)be in the class(λ,ϕ).Then
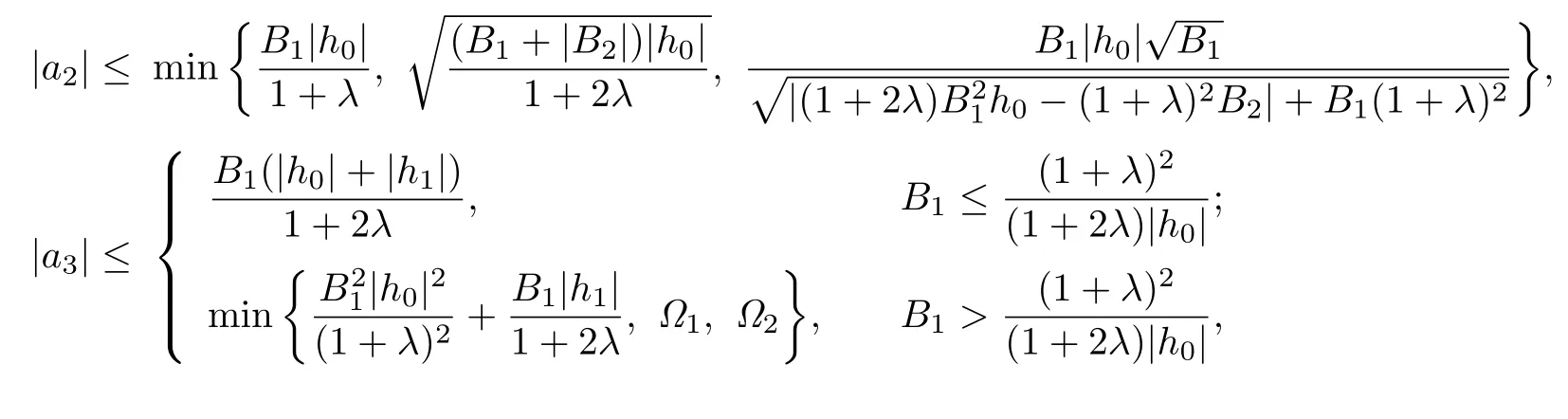
where

Remark 3.5The estimates for|a2|and|a3|asserted by Corollary 3.5 are more accurate than those given by Theorem 2.2 in[14].
Setting h(z)=λ=α=1 in Theorem 2.1,we have the following corollary.
Corollary 3.6Let f(z)given by(1.1)be in the class Ha,b;c
Σ (ϕ).Then
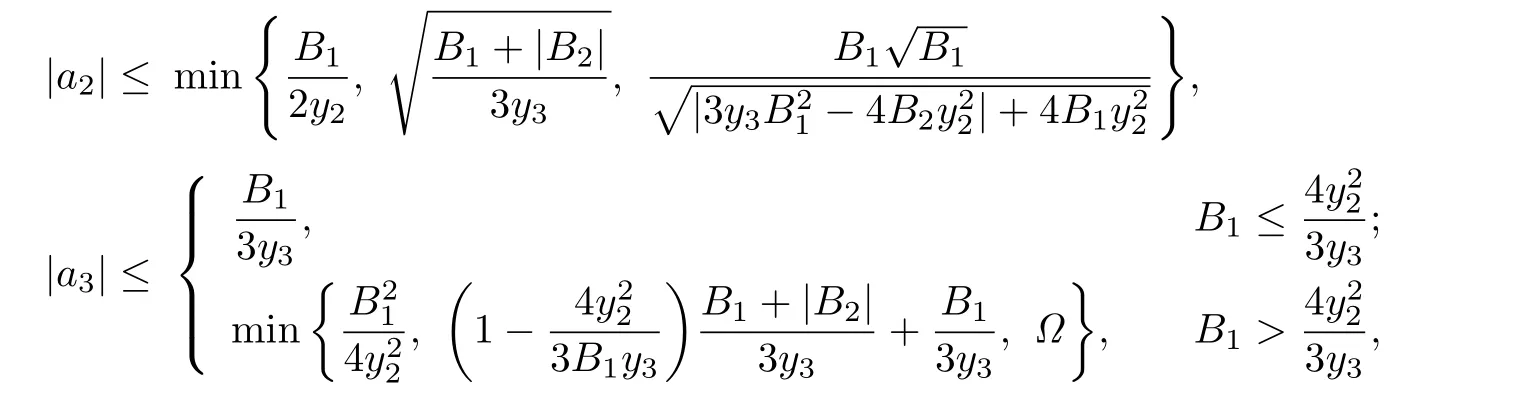
where
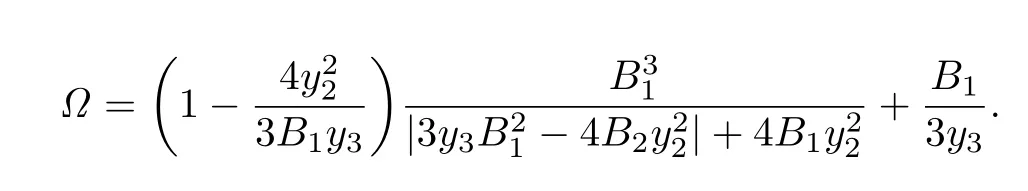
Remark 3.6The estimates for|a2|and|a3|asserted by Corollary 3.6 are more accurate than those given by Theorem 1 in[15].
Setting a=c and b=λ=1 in Theorem 2.1,we have the following corollary.
Corollary 3.7Let f(z)given by(1.1)be in the class Jqα(ϕ).Then
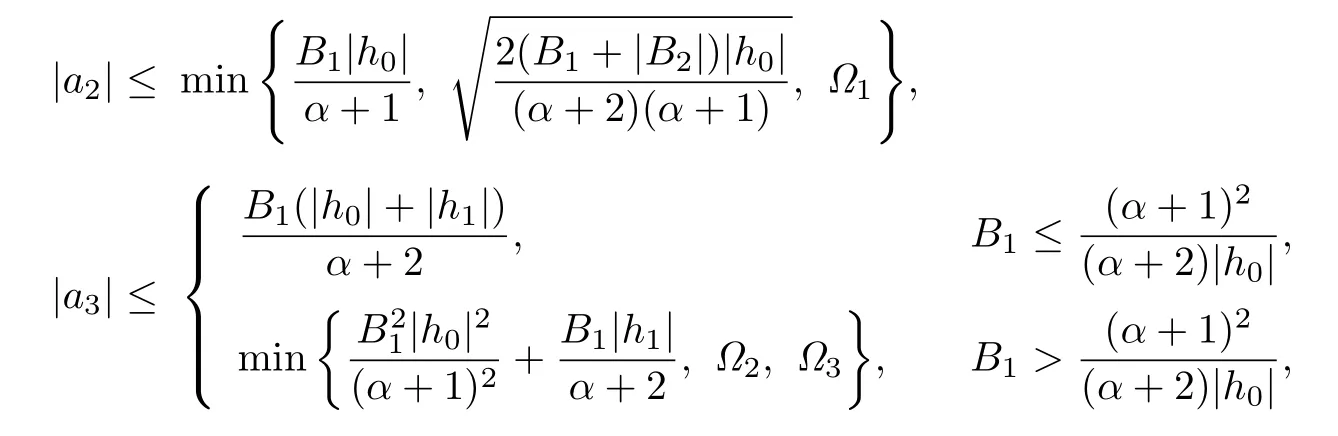
where
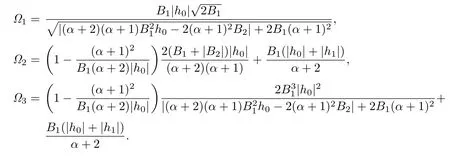
Remark 3.7The estimates for|a2|and|a3|asserted by Corollary 3.6 are more accurate than those given by Theorem 2.1 in[16].
Setting a=c,b=λ=1 and α=0 in Theorem 2.1,we have the following corollary.
Corollary 3.8Let f(z)given by(1.1)be in the class S∗q(Σ,ϕ).Then
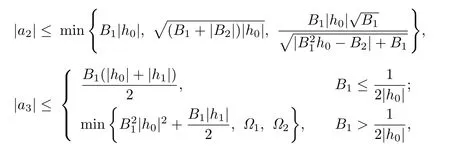
where

Remark 3.8The estimates for|a2|and|a3|asserted by Corollary 3.8 are more accurate than those given by Theorem 2.5 in[17].
Taking δ=1 and δ=0 in Theorem 2.2,we have the following corollaries.
Corollary 3.9Let f(z)given by(1.1)be in the class Ja,b,c
q,Σ(λ,α,ϕ).Then
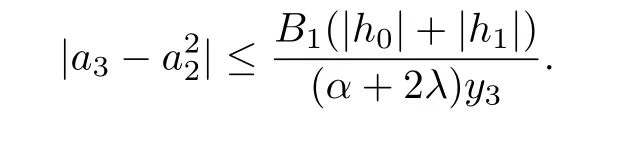
Corollary 3.10Let f(z)given by(1.1)be in the class Ja,b,c
q,Σ(λ,α,ϕ).Then

where
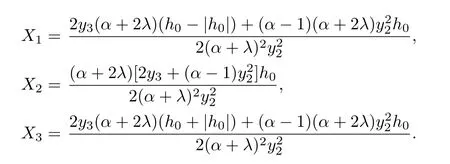
Setting a=c and b=h(z)=α=1 in Corollary 3.10,Corollary 3.10 reduces to the Corollary 33 in[19],which we recall here as Corollary 3.11.
Corollary 3.11Let f(z)given by(1.1)be in the class BΣ(λ,ϕ).Then
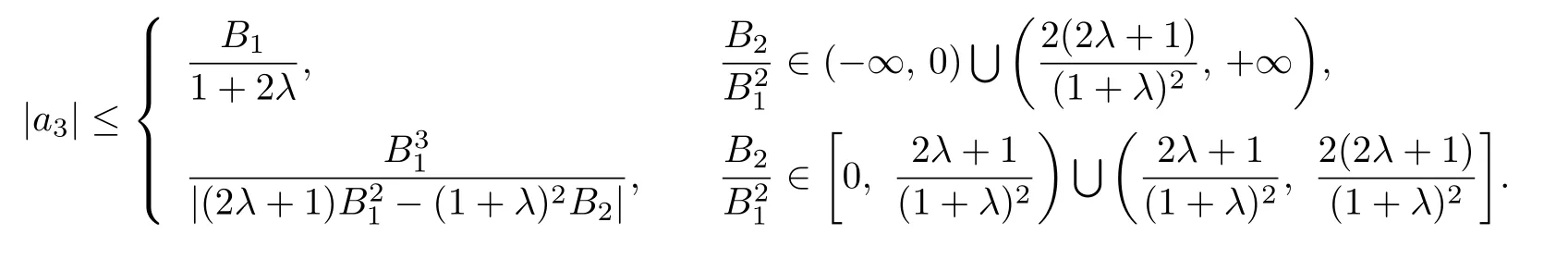
Remark 3.9Setting λ=1 in Corollary 3.11,Corollary 3.11 reduces to the Corollary 8 in[19].
Setting a=c,b=λ=1 and α=0 in Corollary 3.10,Corollary 3.10 reduces to the
Corollary 24 in[19],which we recall here as Corollary 3.12.
Corollary 3.12Let f(z)given by(1.1)be in the class S∗(Σ,ϕ).Then
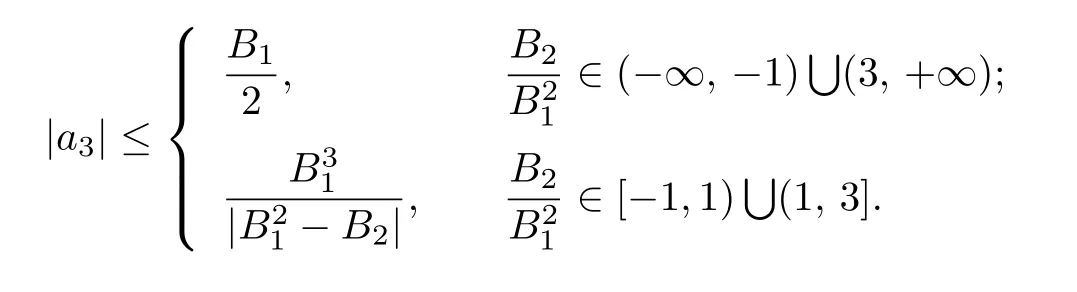
Setting a=c and b=α=1 in Theorem 2.2,we have the following corollary.
Corollary 3.13Let f(z)given by(1.1)be in the class RqΣ(λ,ϕ).Then
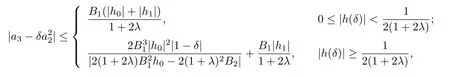
where

Remark 3.10(1) Setting h(z)=1 in Corollary 3.13,Corollary 3.13 reduces to the Corollary 29 in[19].
(2) Setting h(z)=λ=1 in Corollary 3.13,Corollary 3.13 reduces to the Corollary 4 in[19].
Setting a=c and b=λ=1 in Theorem 2.2,we get the following corollary.
Corollary 3.14Let f(z)given by(1.1)be in the class Jqα(ϕ).Then
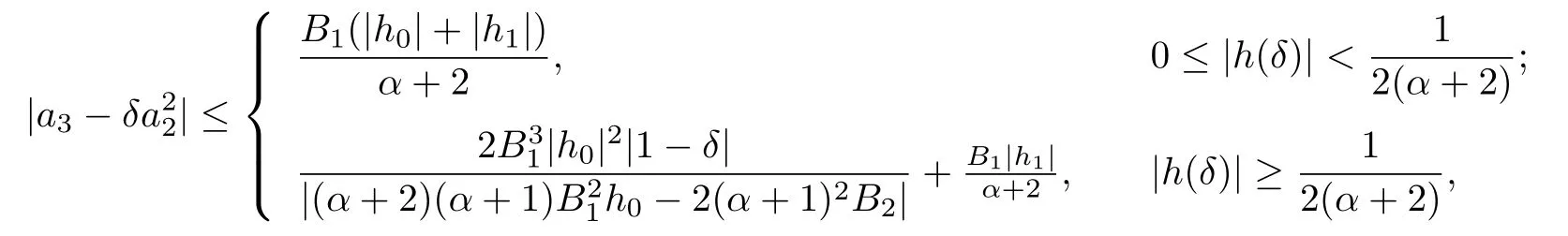
where
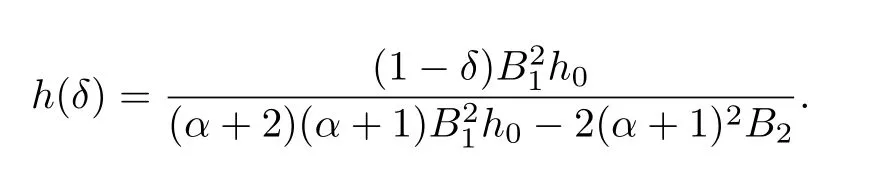
 Communications in Mathematical Research2019年3期
Communications in Mathematical Research2019年3期
- Communications in Mathematical Research的其它文章
- A Nearly Analytic Discrete Method for One-dimensional Unsteady Convection-dominated Diffusion Equations
- Multiple Positive Solutions to Singular Fractional Differential System with Riemann-Stieltjes Integral Boundary Condition
- Planar Cubic G1 Hermite Interpolant with Minimal Quadratic Oscillation in Average
- An SIRS Epidemic Model with Pulse Vaccination,Birth Pulse and Logistic Death Rate
- The Transfer Ideal under the Action of a Nonmetacyclic Group in the Modular Case
- Further Results on Meromorphic Functions and Their nth Order Exact Differences with Three Shared Values
