Multiple Positive Solutions to Singular Fractional Differential System with Riemann-Stieltjes Integral Boundary Condition
Zhang Hai-yan and Li Yao-hong
(1.School of Mathematics and Statistics,Suzhou University,Suzhou,Jiangsu,234000)
(2.School of Mathematics,Anhui University,Hefei,230601)
Communicated by Ji You-qing
Abstract: In this paper,we study a class of singular fractional differential system with Riemann-Stieltjes integral boundary condition by constructing a new cone and using Leggett-Williams fixed point theorem.The existence of multiple positive solutions is obtained.An example is presented to illustrate our main results.
Key words: fractional differential equation,positive solution,integral boundary condition,fixed point theorem
1 Introduction
In recent years,the theory of integral boundary value problems have been studied widely and there are many excellent results(see[1]–[11]and references therein).In[12],by means of the fixed point index theory in cones,the authors obtained the existence and multiplicity of positive solutions for a singular fractional differences equation where α ≥2,is standard Riemann-Liouville derivative,q(t)may be singular at t=0 or t=1,f(t,u)may also be singular at u=0,u(s)dA(s)denotes the Riemann-Stieltjes integral,A is a function of bounded variation.

Recently,the coupled boundary value problems to fractional differential systems were caught much attention.For example,Henderson and Luca[13]investigated the nonexistence of a system of nonlinear Riemann-Liouville fractional differential equations with coupled integral boundary conditions
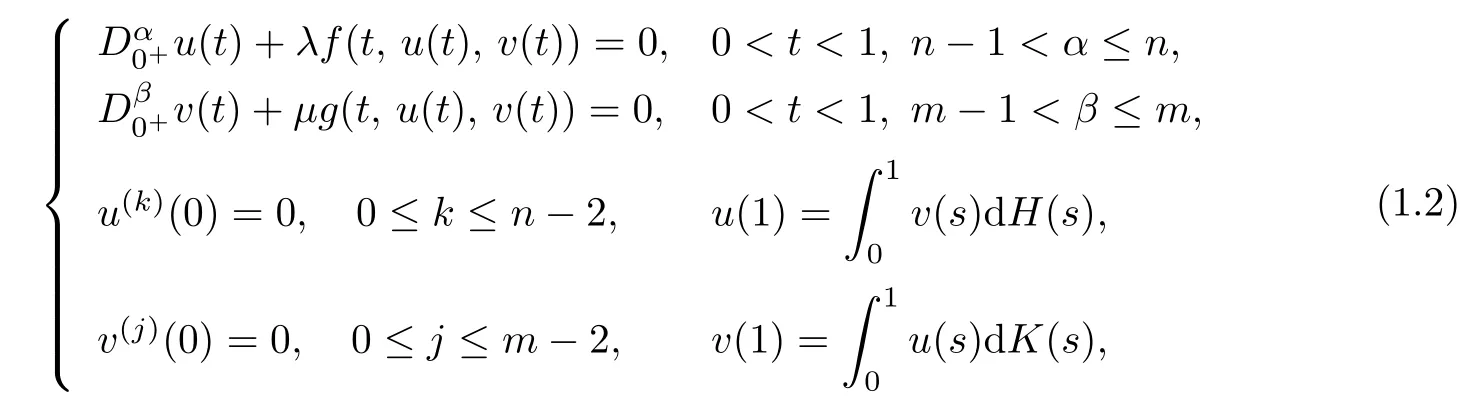
Henderson et al.[14]–[15]also studied the following system with uncoupled integral boundary conditions

Motivated by the aforementioned papers,a natural question is whether the coupled and the uncoupled integral boundary conditions can be unified in a system.If we have unified the conditions,how can we obtain the existence of the solution? This question motivates the study of the existence of multiple positive solutions for the following singular boundary value problems of fractional differential equations:

where αi>2,is the standard Riemann-Liouville derivative,ai(t)∈C((0,1),[0,+∞))may be singular at t=0 and/or t=1,fi∈C([0,1]×[0,+∞)×[0,+∞),[0,+∞)),ni∈Z,ni≥3,i=1,2.The functionals gi∈C([0,+∞)×[0,+∞),[0,+∞))are linear functionals involving Riemann-Stieltjes integrals βi[w]=w(s)dAi(s)with positive measures Ai,i=1,2.
By constructing a new cone and using Leggett-Williams fixed point theorem,we obtain the existence of at least three positive solutions for the problem(1.4). The method we adopt,which is different from[5]–[14]. Moreover,the boundary conditions we considered here is general,which unified the coupled and the uncoupled form.The rest of the paper is organized as follows:In Section 2,we present some preliminaries and several lemmas.In Section 3,we obtain the existence of at least three positive solutions for(1.4)and we give an example to illustrate our results.
2 Preliminaries and Lemmas
In this section,we present preliminaries and lemmas which are useful to the proof of our main results.
Definition 2.1The Riemann-Liouville fractional derivative of order α for a continuous function f is given by provided that the right-hand side is pointwise defined on(0,+∞).

Definition 2.2The Riemann-Liouville fractional integral of order α for a function f is given by
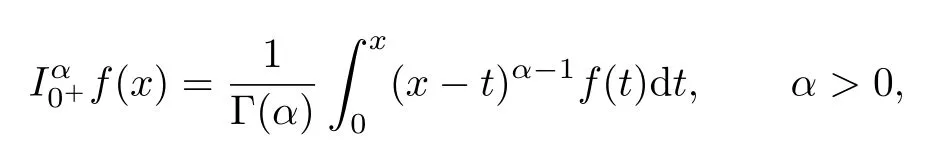
provided that the integral exists.
Lemma 2.1[16]Let α>0.Then the following equality holds for u ∈L(0,1),u(t)∈L(0,1):

where ci∈R,
n −1<α ≤n.
Lemma 2.2Let yi(t)∈L(0,1),i=1,2.Then the unique solution of the following fractional boundary value problem

has an integral representation
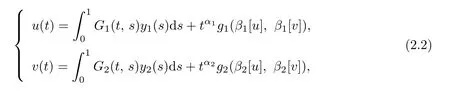
where
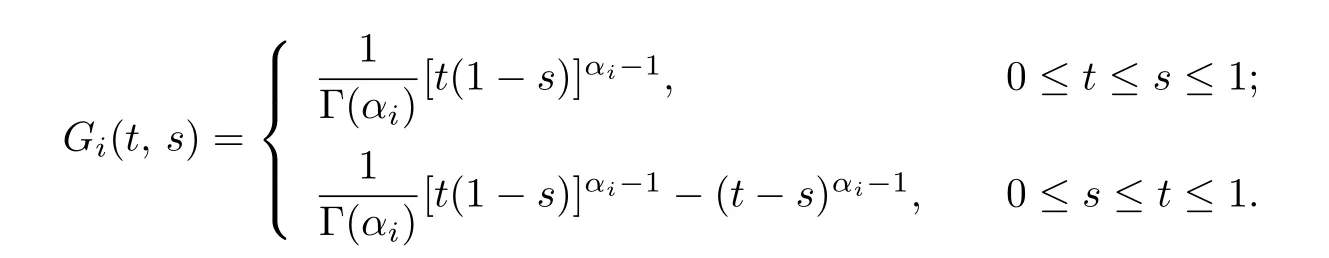
Proof. By means of the Lemma 2.1,we can reduce(2.1)to an equivalent system of integral equations

Applying the conditions
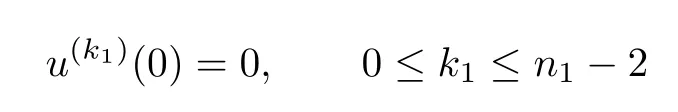
and

we have

and

So
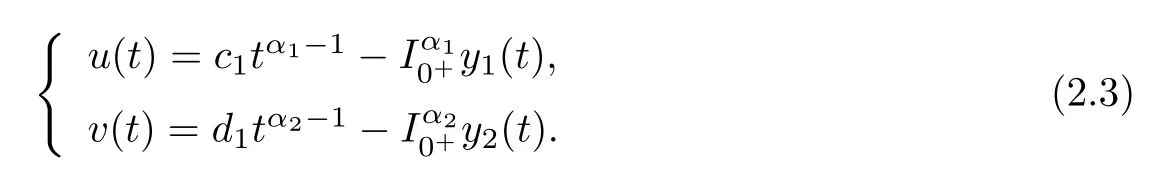
Combining with the conditions

and letting t=1 in(2.3),we have

Substituting(2.4)into(2.3),we have

This completes the proof.
Lemma 2.3[17]The function Gi(t,s)satisfies:
(1)Gi(t,s)>0 for all t,s (0,1),i=1,2;
(2)ci(t)ψi(s)Gi(t,s) ∈ψi(s)for all(t,s)[0,1],i=1,2,
where

Remark 2.1Set[ξ,η]⊂(0,1).Let γ:=min{ci(t):t ∈[ξ,η],i=1,2}.
It is easy to see that 0<γ ≤ci(t) From Lemma 2.3,we have Let E=C[0,1]C[0,1]be endowed with the norm Let and It is easy to see that P and K are cones in E.Define the operator T:K →E by T(u,v)(t)=(T1(u,v)(t),T2(u,v)(t)), t ∈[0,1], where Ti(u,v)(t)(i=1,2)are given by We make the following assume throughout this paper: (H1) ai(t):(0,1)[0,+)is continuous,ai(t)0, where ψi(s)are defined by Lemma 2.3. Lemma 2.4The operator T:K →K is a completely continuous operator. Proof. First,we prove the operator T:K →K. Since Gi,ai,fi,gi≥0,we have Ti(u,v)(t)≥0, (u,v)∈K,t ∈[0,1],i=1,2. By(2.5)and Lemma 2.3,we have On the other hand,it follows Lemma 2.3,Remark 2.1 and(2.6),we have Hence This implies that T(u,v)=(T1(u,v),T2(u,v))∈K,that is,T:K →K. Notice that T1(u,v)(t),T2(u,v)(t)are continuous on[0,1].Obviously,operator T is also continuous.Define a ball in cone K by BR={(u,v)|(u,v)∈E,∥(u,v)∥≤R}, and set Ω=[0,1]×BR.Let Then,for any(u,v)∈BR,t ∈[0,1],we have which implies that TBRis uniformly bounded. Secondly,we prove that operator T is equicontinuous. For all t1,t2∈[0,1],t2>t1and(u,v)∈BR,we have In view of(2.10),letting t1→t2,then ∥Ti(u,v)(t2)−Ti(u,v)(t1)∥→0, i=1,2. That is,as t1→t2, ∥T(u,v)(t2)−T(u,v)(t1)∥=∥T1(u,v)(t2)−T1(u,v)(t1)∥+∥T2(u,v)(t2)−T2(u,v)(t1)∥→0. So we prove that T(BR)is an equicontinuous set. According to standard application of Ascoli-Arzel`a theorem,we can obtain that T:K →K is a completely continuous operator. Lemma 2.5[18]Let P be a cone in a real Banach space E,={x ∈P|∥x∥≤c},β be a nonnegative continuous concave functional on P such that β(x)≤∥xfor all x ∈and P(β,b,d)={x ∈P|b ≤β(x),∥x∥ (A1) {x ∈P(β,b,d):β(x)>b}=∅and β(Ax)>b for x ∈P(β,b,d); (A2)∥Ax∥ (A3) β(Ax)>b for x ∈P(β,b,c)with ∥Ax∥>d. Then A has at least three fixed points x1,x2,x3insatisfying ∥x1∥ Define the nonnegative continuous concave functional β(u,v)on the cone K by β(u,v)= For convenience,we introduce the following notations: Then 0 ≤mi≤Mi, i=1,2. Theorem 3.1Suppose that the condition(H1)is satisfied,and there exist positive con stants and If fi(t,u,v),gi(x,y)satisfy the following growth conditions: then(1.4)possesses at least three positive solutions(u1,v1),(u2,v2),(u3,v3)satisfying and Proof. From Lemma 2.2,it is readily seen that fixed points of the operator(2.5)are solutions of the system(1.4). In order to apply Lemma 2.5,we divide the proof into four steps. Step 1.Set ¯Kc={(u,v)|(u,v)∈K,∥(u,v)∥≤c}. Consequently,by condition(H3),we have Combining with Lemma 2.4,we know that T:→is a completely continuous operator. Step 2.Let It is easy to see that which implies that From assumption(H4)of Theorem 3.1,we have This implies that condition(A1)of Lemma 2.5 is satisfied.Step 3.Set Similar argument with the first step,by condition(H5),we have ≤ Hence,the condition(A2)of Lemma 2.5 is satisfied. Then Therefore,condition(A3)of Lemma 2.5 is satisfied. Thus,all conditions of Lemma 2.5 are satisfied. Then(1.4)has at least three positive solutions(u1,v1),(u2,v2),(u3,v3)such that ∥(u1,v1)∥ and ∥(u3,v3)∥>a witht∈m[ξin,η](u3(t)+v3(t)) This proof is completed. Example 3.1Consider the following singular boundary value problems of system of fractional differential equations where and Consequently,by Lemma 2.2,we have By Lemma 2.3,we have Choose[ξ,η]=[0.6,0.8].By a direct calculation,we can obtain γ ≈0.0279,M1≈0.4515,m1≈0.0431,M2≈0.3010,m2≈0.0313,L1=1,L2=0.5,β1[1]=1,β2[1]=2. Choose q1=5,q2=4,p1=5,p2=7,a=1,b=4,c=800.It is easy to verify that all the conditions of Theorem 3.1 hold. Thus,by Theorem 3.1,the system(3.4)has at least three positive solutions(u1,v1),(u2,v2),(u3,v3)such that ∥(u1,v1)∥<1,4<{(u2,v2)}and ∥(u3,v3)∥>1 with{(u3,v3)}<4.
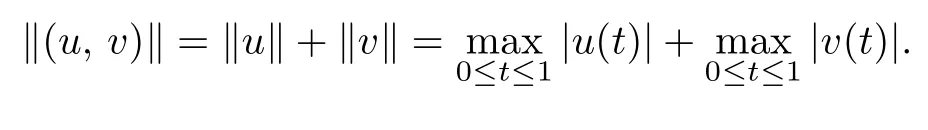


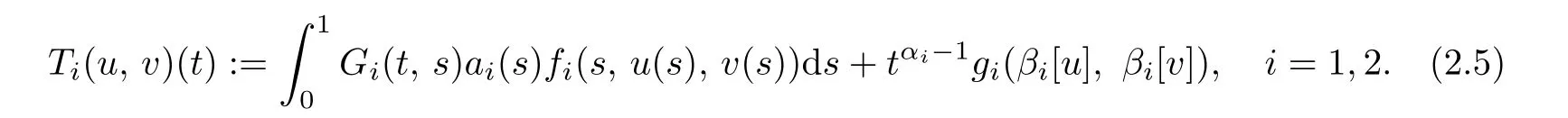
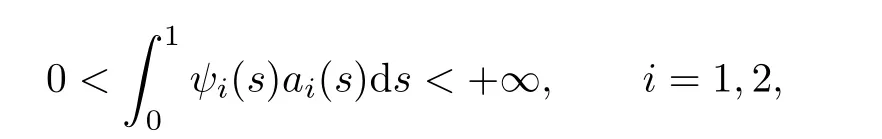

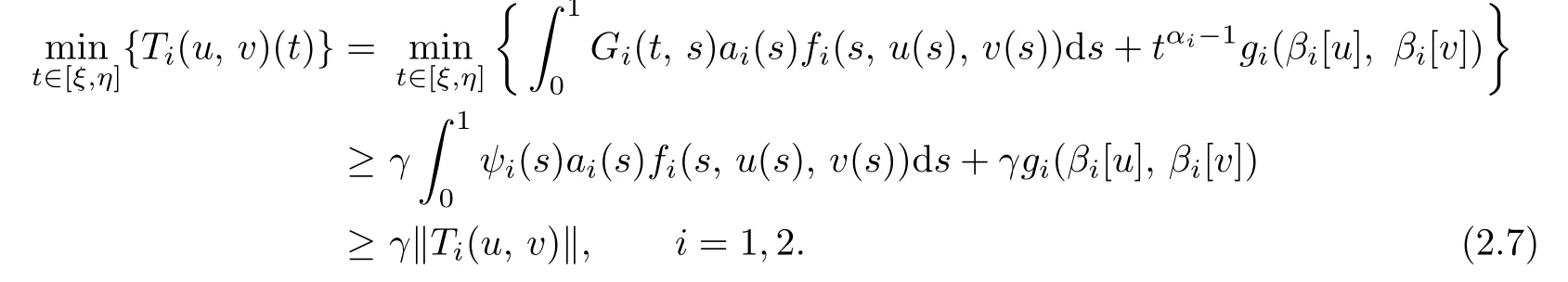
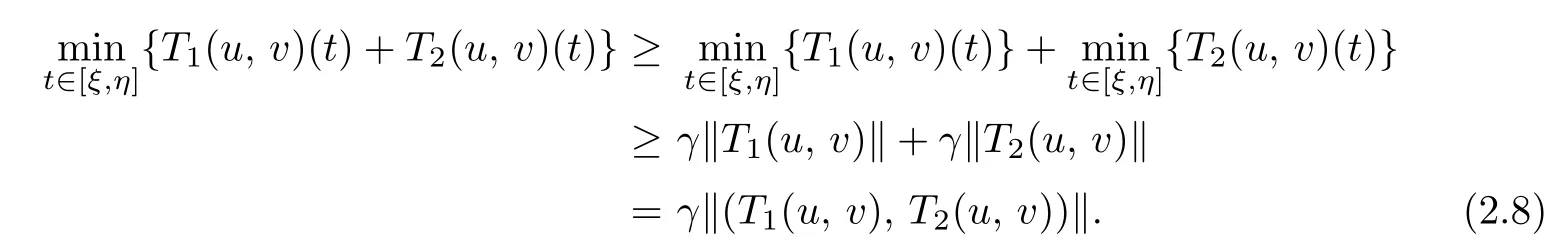
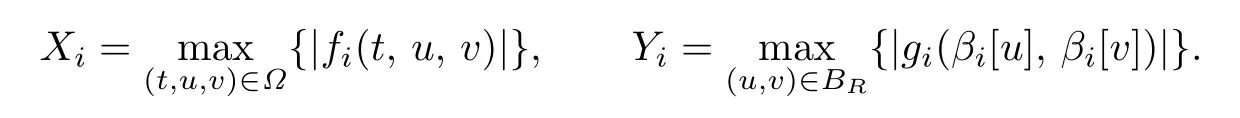
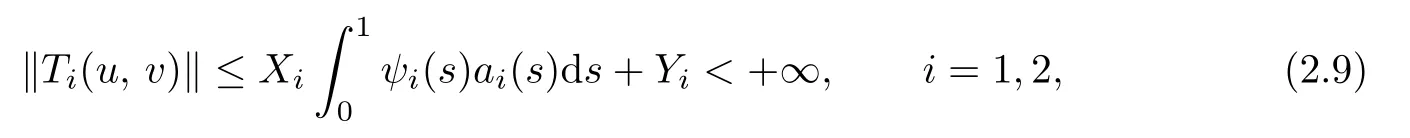

3 Main Result


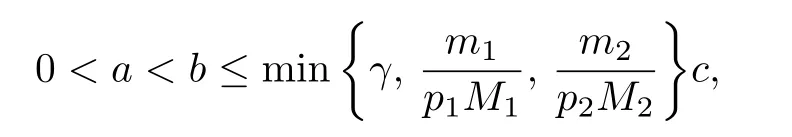


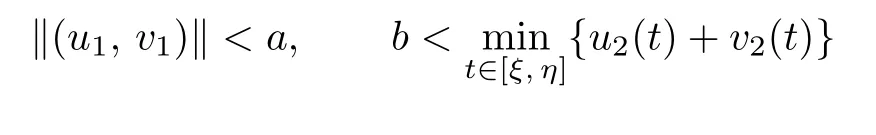



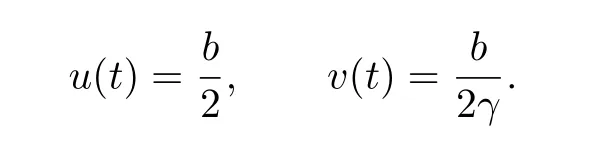


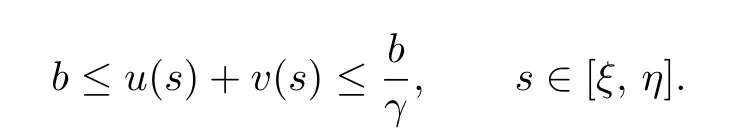

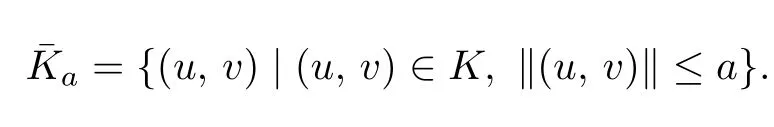



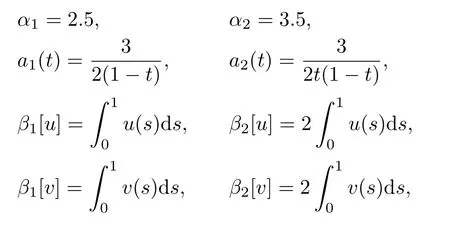
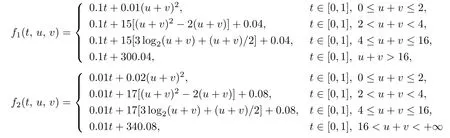



 Communications in Mathematical Research2019年3期
Communications in Mathematical Research2019年3期
