The Transfer Ideal under the Action of a Nonmetacyclic Group in the Modular Case
Jia Pan-pan and Nan Ji-zhu
(School of Mathematics,Dalian University of Technology,Dalian,Liaoning,116024)
Communicated by Du Xian-kun
Abstract:Let Fq be a finite field of characteristic p(p /=2)and V4 a four-dimensional Fq-vector space.In this paper,we mainly determine the structure of the transfer ideal for the ring of polynomials Fq[V4]under the action of a nonmetacyclic p-group P in the modular case.We prove that the height of the transfer ideal is 1 using the fixed point sets of the elements of order p in P and that the transfer ideal is a principal ideal.
Key words:invariant,p-group,coinvariant,transfer ideal,principal ideal
1 Introduction
Let V be a vector space of dimension n over a field F and we choose a basis,{x1,x2,,xn},for the dual,V∗,of V.Let ρ:GGL(n,F)be a faithful representation of a finite group G. The action of G on V induces an action on V∗which extends to an action by algebra automorphisms on the symmetric algebra of V∗,
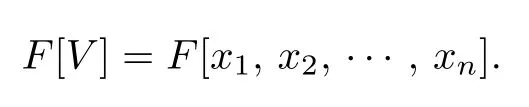
Specially,for every g ∈G,f ∈F[V]and v ∈V,
(g·f)(v)=f(ρ(g−1)v).
The ring of polynomial invariants of G is the subring of F[V]given by
F[V]G:={f ∈F[V]|gf=f,g ∈G}.
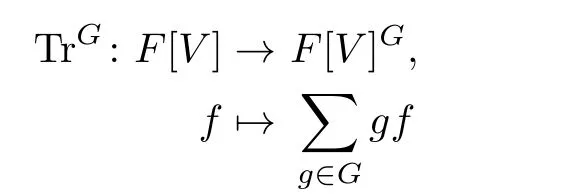
The transfer homomorphism is defined by and it is a homomorphism of F[V]G-modules. It is surjective in the nonmodular case,where it provides a tool for constructing the ring of polynomial invariants F[V]G. In the modular case,the image of the transfer Im(TrG)⊆F[V]Gis a proper,non-zero ideal[1].This makes the transfer ideal an interesting object of study and inspired quite a number of research. Campbell[2]proved that the transfer ideal is a principal ideal for GLn(Fq)and Un(Fq)using block bases,where Fqdenotes the finite field.He also proved that the transfer ideal is in general not principal for Σn.Neusel[3],[4]discussed the transfer for permutation representations. She proved that the transfer ideal for cyclic p-groups is a prime ideal of height at most n−k,where k denotes the number of orbits of a permutation basis.She also showed that the transfer ideal for permutation representations of finite groups is generated by the transfers of special monomials.And this leads to a description of the transfer ideal for the alternating groups.In this paper,we discuss the transfer ideal for a nonmetacyclic p-group.
The group P defined by generators a,b,c and the relations is a nonmetacyclic p-group.It is easy to see that
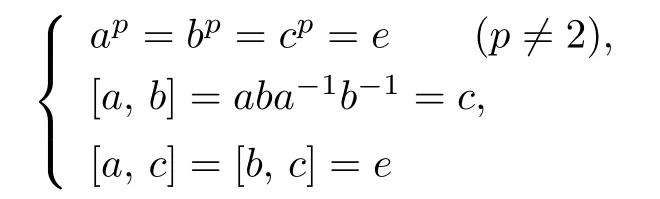
P={aibjck|0 ≤i,j,k ≤p −1},
and the order of every element is p except the identity element,whence|P|=p3. The p-group P is the nonabelian p-group of smallest order(see[5]).In Section 2,we introduce a faithful representation ϕ:PGL(4,Fq)of P over the field Fq.Here Fqdenotes the field with q elements and the characteristic of Fqis p(p /=2). For the representation of finite p-groups in characteristic p,there is always a Dade basis(see[1]).So we can construct a system of parameters for the ring of polynomial invariants Fq[V4]Pby finding a Dade basis.Moreover,the product of the degrees of the system of parameters is equal to the order of P,so the system of parameters can generate Fq[V4]P.Then we calculate the ring of coinvariants Fq[V4]Pand show that it is not the regular representation.In Section 3,we first calculate the fixed point sets of the elements of order p in group P and obtain the height of the transfer ideal is 1,i.e.,ht(Im(TrP))=1.The image of a set of module generators for F[V]as a F[V]G-module under the transfer map can generate the transfer ideal.We show that Fq[V4]is a free Fq[V4]P-module.Furthermore,we use this result to prove that the transfer ideal Im(TrP)is a principal ideal.
2 The Ring of Invariants and the Ring of Coinvariants
First,we introduce a faithful representation ϕ:PGL(4,Fq)of P over the field Fq.
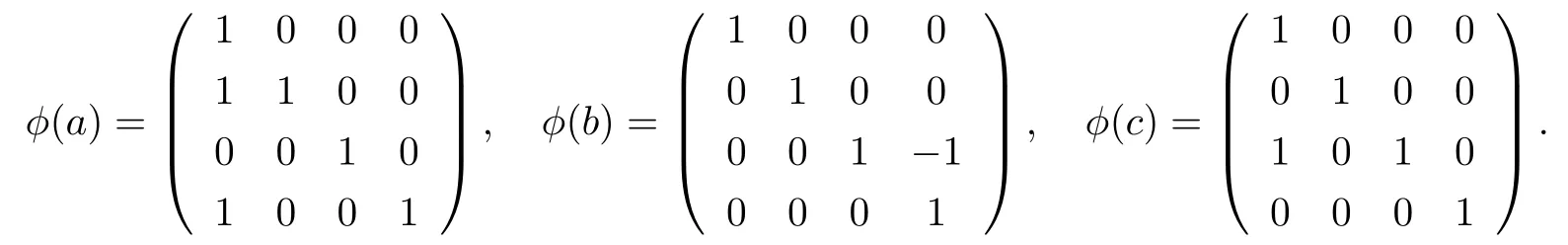
The representation space is V4=.Let e1,e2,e3,e4be a basis for V4,and x,y,z,w a basis for the dual spaceof V4.So we denote
Fq[V4]=Fq[x,y,z,w],
and we have

It follows that the orbits of P on x,y,z,y −w are
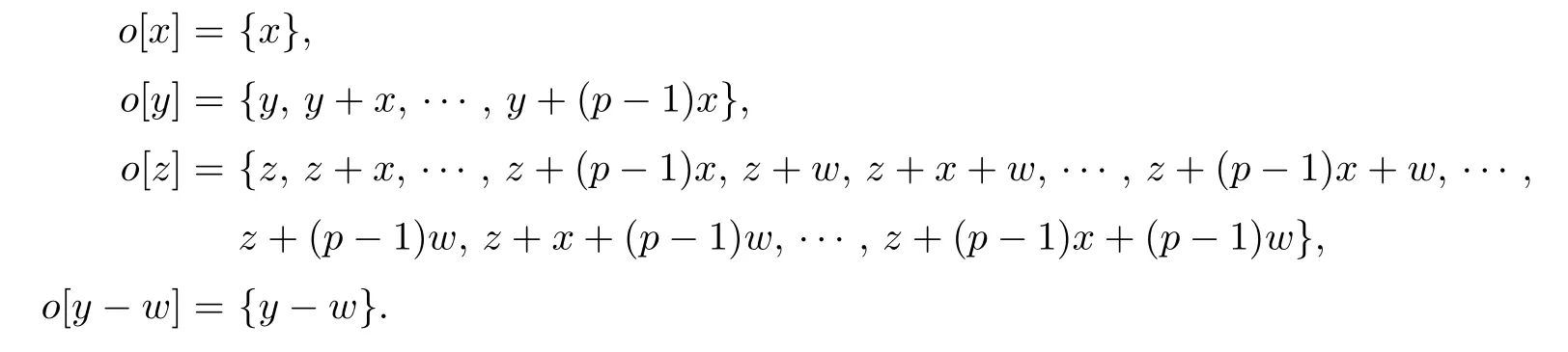
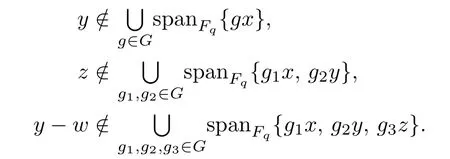
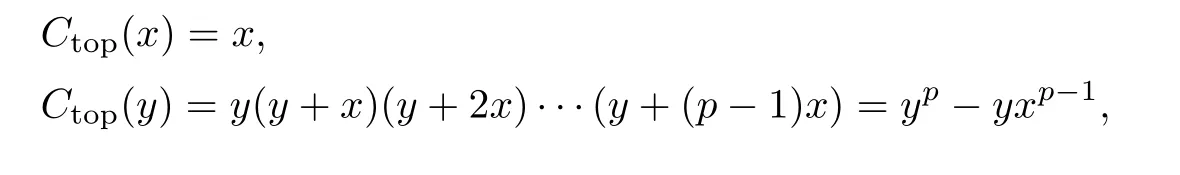
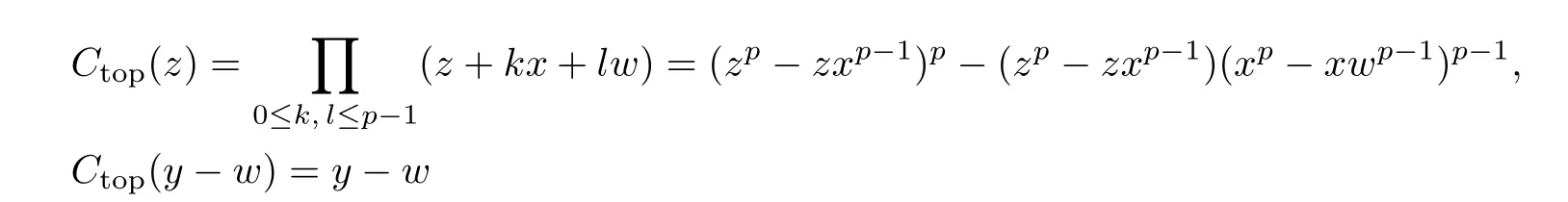
Then the top Chern classes − −of the orbits o[x],o[y],o[z],o[y −w]is a system of parameters.And we have
|P|=deg(Ctop(x))·deg(Ctop(y))·deg(Ctop(z))·deg(Ctop(y −w))=p3.Hence
Fq[V4]P=Fq[x,yp−yxp−1,(zp−zxp−1)p−(zp−zxp−1)(xp−xwp−1)p−1,y −w].From the above we have
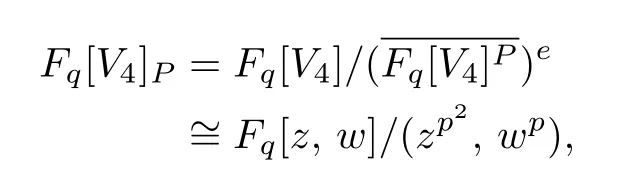
where Fq[V4]P={f ∈Fq[V4]P
|deg(f)>0}denotes the augmentation ideal of Fq[V4]P,and(Fq[V4]P)edenotes the extension ideal of Fq[V4]Pin Fq[V4].The ring of coinvariants Fq[V4]Pis finite-dimensional vector space over Fq.It is easy to see that z2+(zp2,wp),zw+(zp2,wp)and w2+(zp2,wp)are linearly independent,so z2+(zp2,wp),zw+(zp2,wp),w2+(zp2,wp)is a basis for Fq[V4]P(2).In the same manner we have that{1+(zp2,wp)},{z+(zp2,wp),w+(zp2,wp)},{z2+(zp2,wp),zw+(zp2,wp),w2+(zp2,wp)},,{zp2
−1wp−1+(zp2,wp)}are the bases for the homogeneous component of the ring of coinvariants Fq[V4]P.But
a(z+(zp2,wp))=z+(zp2,wp),a(w+(zp2,wp))=w+(zp2,wp),hence it is not a faithful representation.
Proposition 2.1The ring of coinvariants Fq[V4]Pis not the regular representation of the group P.
Proof. The ring of coinvariants Fq[V4]Pis not a faithful representation,obviously the regular representation is faithful.
3 The Transfer Ideal
In this section,we first calculate the fixed point sets of the elements of order p in group P according to the followings to prove that the height of Im(TrP)is 1.
Definition 3.1[1]Let ρ:GGL(n,F)be a faithful representation of a finite group G over a field F.The transfer variety ΩGis the subset of V given by
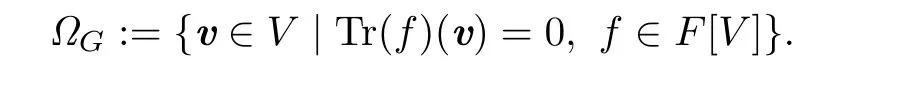
Since Im(TrG)is an ideal of F[V]Gand F[V]GF[V]is a ring extension,we have by the definition of transfer variety.
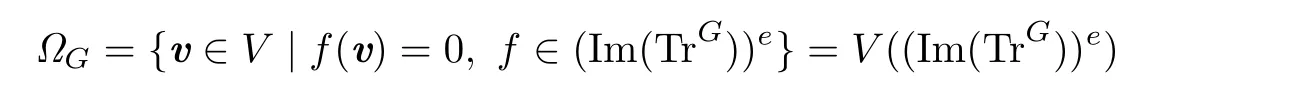
Lemma 3.1[1]Let ρ:GGL(n,F)be a faithful representation of a finite group G over a field F of characteristic p.Then we have
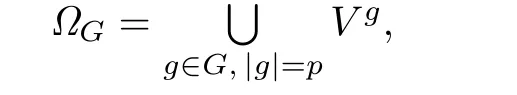
where Vg⊆V is the fixed point set of the element g ∈G acting on V.
Let g ∈GL(n,F),and we define
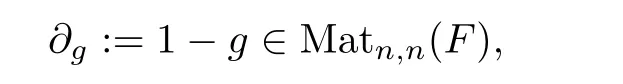
where Matn,n(F)denotes the algebra of n×n matrices over F.Let Ig⊆F[V]denote the ideal of F[V]generated by ∂g(V∗),where V∗is the dual space of V=Fn,regarded as the homogeneous component of F[V]of degree 1,i.e.,as the homogeneous linear forms in F[V].
Lemma 3.2[1]Let g ∈GL(n,F),and V(Ig)⊆V be the affine variety defined by the ideal Ig⊆Tot(F[V]).Then V(Ig)=Vg.
We can replace a graded object A by its totalization defined by Tot(A)=⊕Ai,thereby throwing away the grading.
Theorem 3.1[1]Let ρ:GGL(n,F)be a representation of a finite group over the field F of characteristic p.Then

and the ideals ℘g=Ig∩F[V]Gare prime,where g ∈G and the order of g is p.Hence
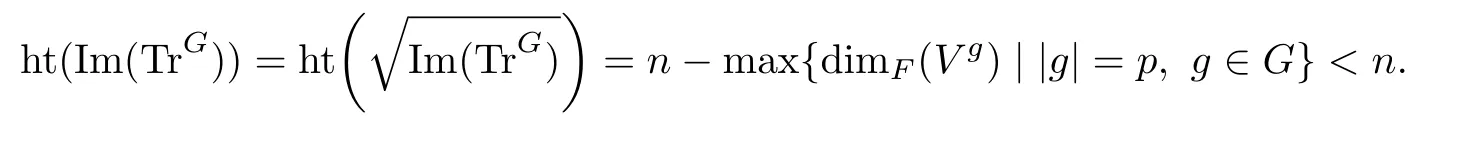
Proposition 3.1The fixed point sets of the elements of order p in group P are listed as follows:

Proof. We first show that
Va4={λ1e2+λ2e3+λ3e4|λ1,λ2,λ3∈Fq}.
Let λ1e1+λ2e2+λ3e3+λ3e4∈V4,where λ1,λ2,λ3,λ4∈Fq.Since

we have
Then ht(Im(TrP))=1 is an immediate consequence of Theorem 3.1.
Next,we introduce some preliminaries to prove that Im(TrP)is a principal ideal.Lemma 3.3[7]Let=prbe a prime power and suppose that l is a positive integer.Then

It follows that
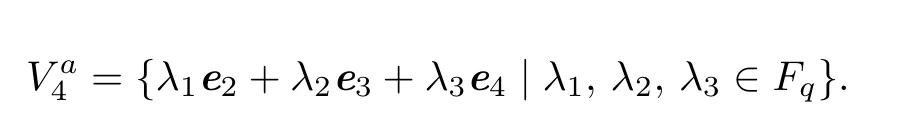
We next prove that
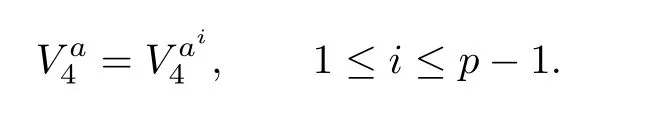

Consequently,
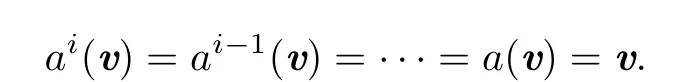
Conversely,it is easily seen that aiis the generator of⟨a⟩for every i,then
a=(ai)kfor some kZ.
Similarly,if ai(v)=v,then a(v)=v.Therefore,we have⊆.Similarly,we have
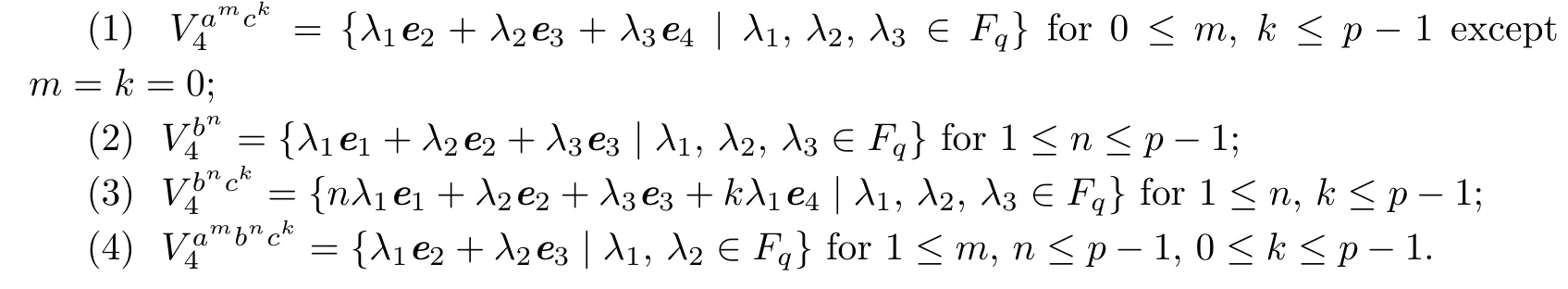
Theorem 3.2ht(Im(TrP))=1.
Proof. From Proposition 3.1 we can see that
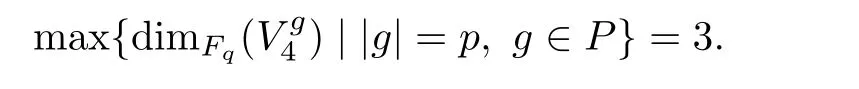
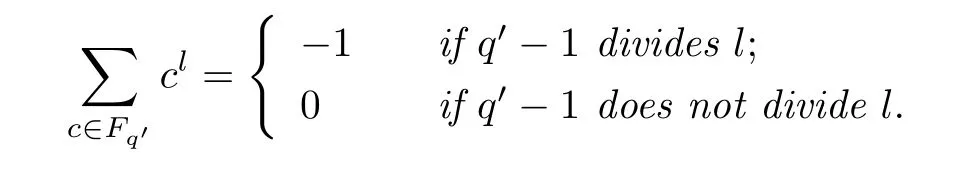
Lemma 3.4Let t,s and j be positive integers.Suppose that(t+s)(p −1)≤j ≤p2−1.
Then
(1) if t+s ≤p and j (2)assume that j=(p+1)(p −1)=p2−1. (i) If s+t (ii)if s+t=p+1,then i.e., Proof. As we know, Let α be the number of multiples of p that j!is contained and β be the number of multiples of p that(t(p −1))!(s(p −1))!(j −(t+s)(p −1))!is contained. Since t(p −1),s(p −1),j −(t+s)(p −1)≤j and If t+s ≤p and j so we obtain If j=(p+1)(p 1)=p21,then So,if s+t ≤p,we have Therefore, If s+t=p+1,we have Therefore, Theorem 3.3[1]Let A be a commutative graded F-algebra anda Noether normalization of A.Then the following conditions are equivalent: (1) A is Cohen-Macaulay; (2) a1,,an∈A is a regular sequence; (3) A is a free finitely generated N-module; (4) The Pioncar´e series of A has the form P(A,t)=P(N,t)·P(A//N,t), where A//N=F ⊗N Theorem 3.4Im(TrP)=is a principal ideal. is a Noether normalization of Fq[V4]. Clearly Fq[V4]is Cohen-Macaulay,then Fq[V4]is a free finitely generated Fq[V4]P-module by Theorem 3.3.So we have Since where 1 ≤i ≤p −1,1 ≤j ≤p2−1,so we consider Since where m ∈Fp,0 ≤s ≤i ≤p −1,by Lemma 3.3,we have From these we conclude that We now turn to Lemma 3.3 shows that if p −1 does not divide j1and j2simultaneously,then we have So we suppose that p −1 divides j1and j2simultaneously.From Lemma 3.4 we know that if j if j=p2−1,then if and only if j1+j2=(p+1)(p −1)=j.Hence,if j if j=p21,then For each f ∈Fq[V4], where fi,j∈Fq[V4]P.Therefore, So is a principal ideal.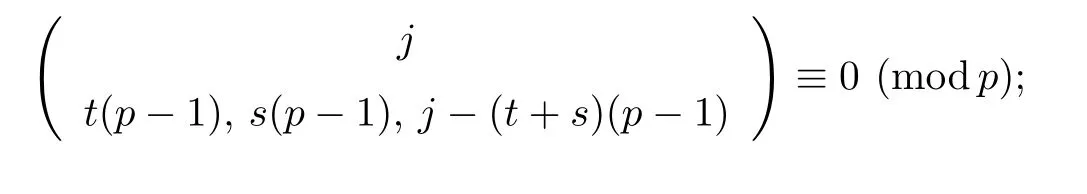

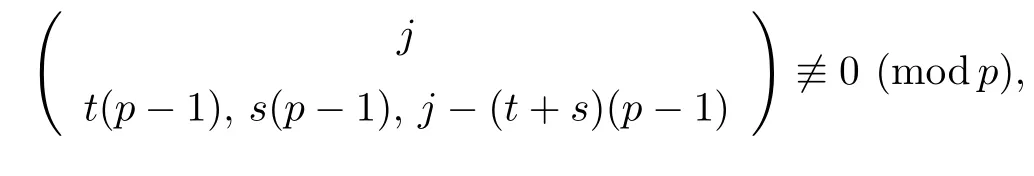

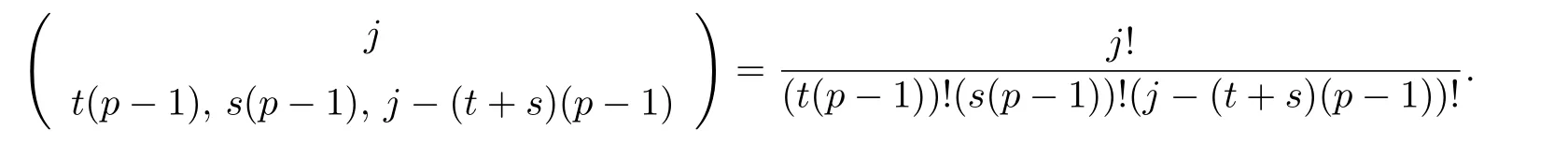
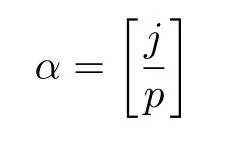
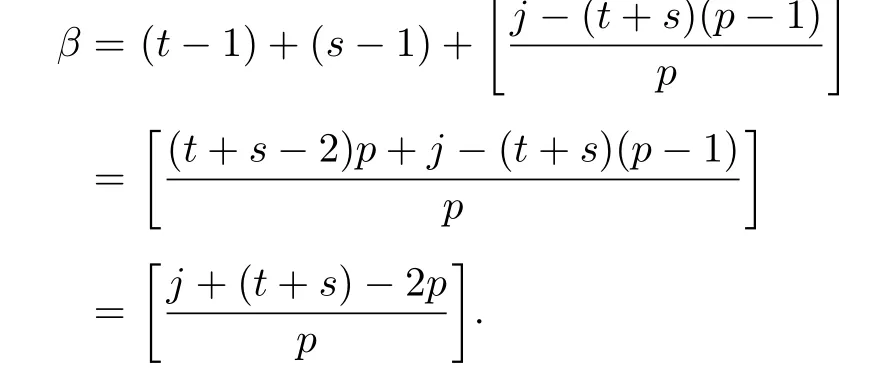
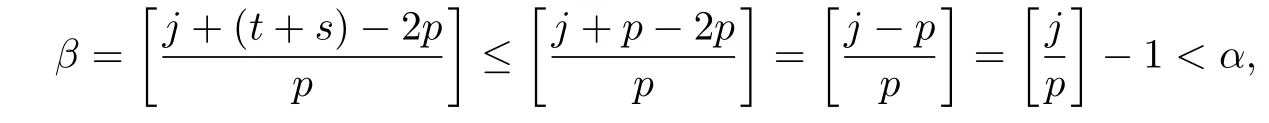

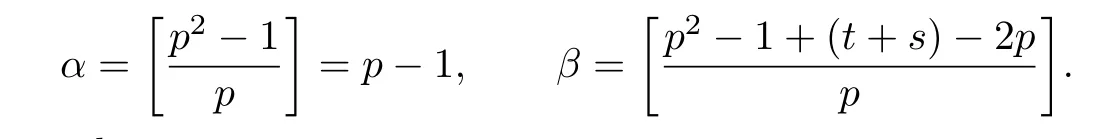

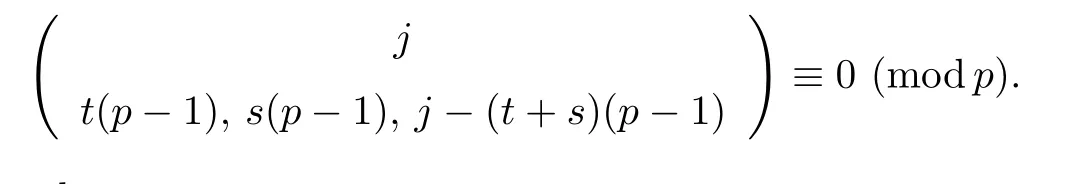

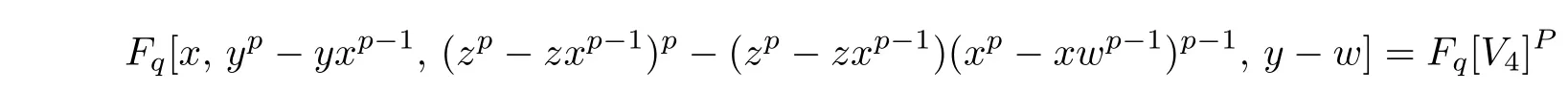


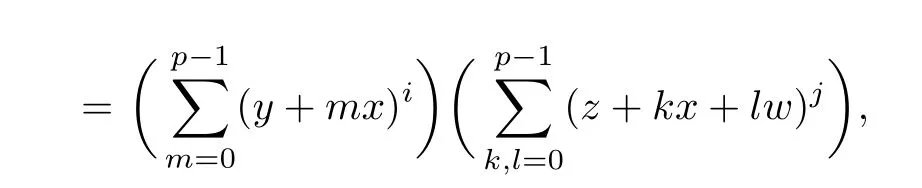
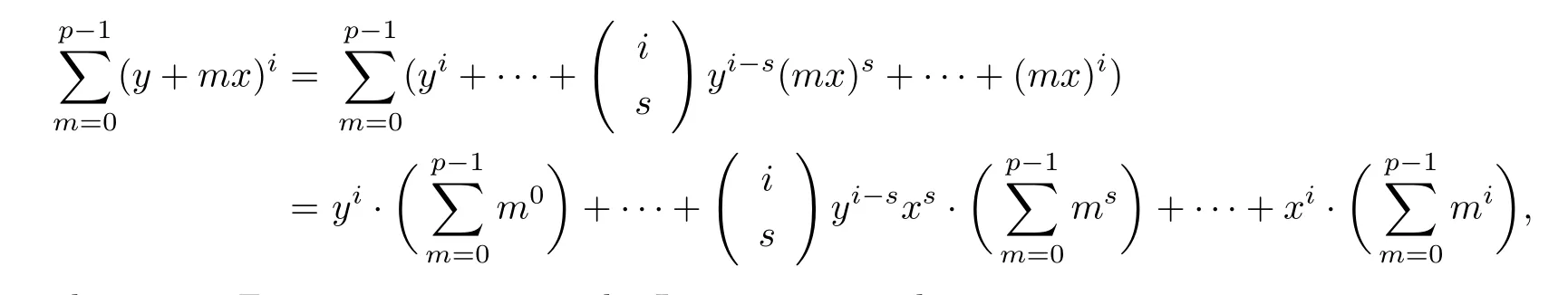
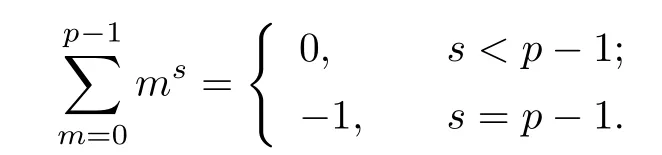
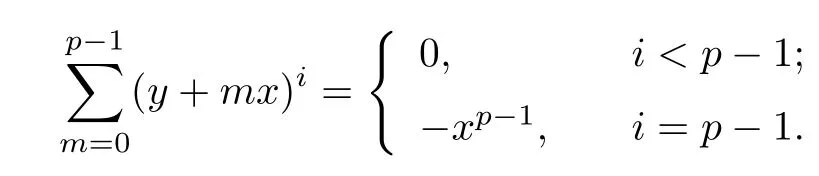
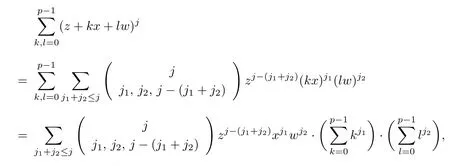

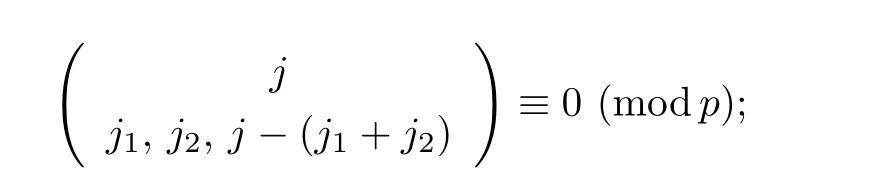
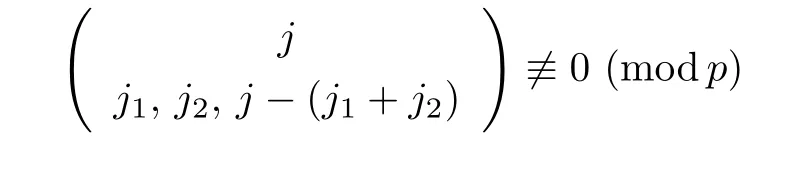
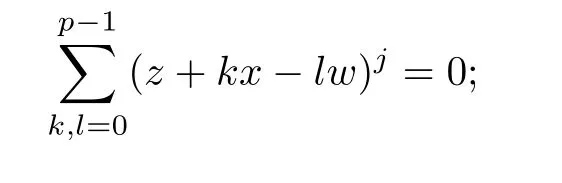
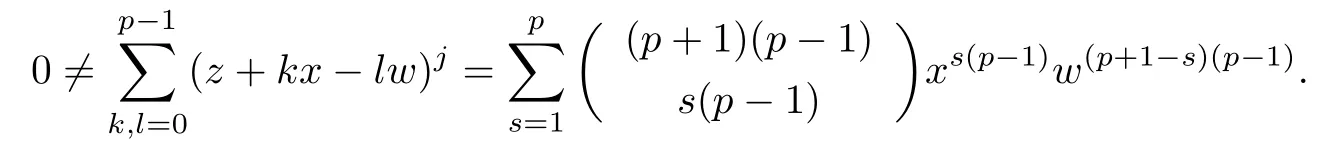
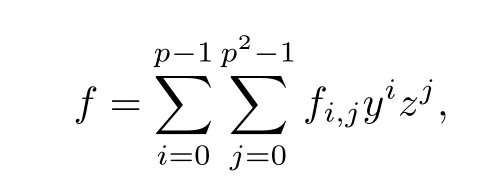
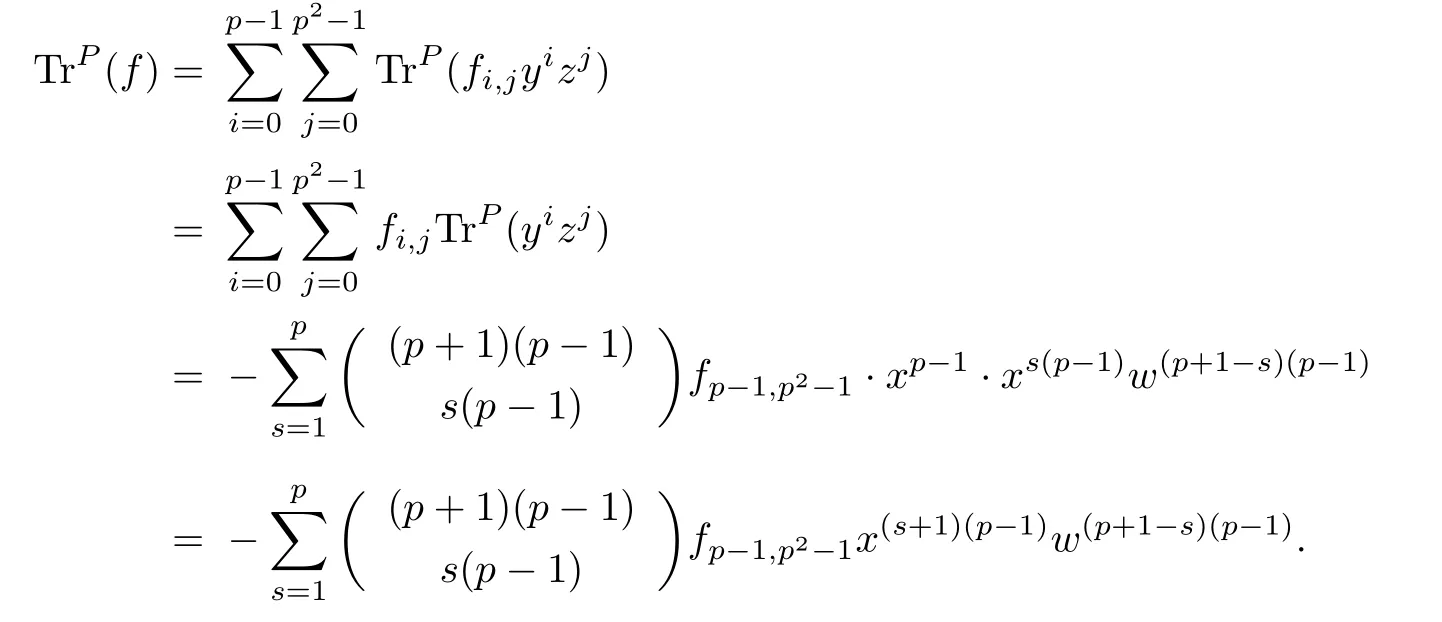
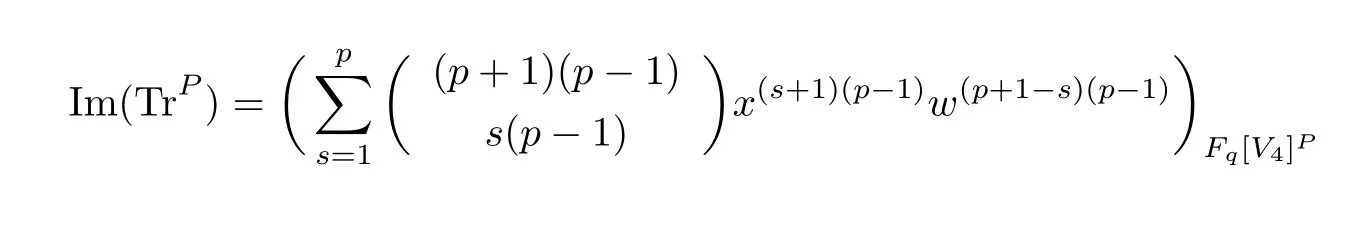
 Communications in Mathematical Research2019年3期
Communications in Mathematical Research2019年3期
