A Nearly Analytic Discrete Method for One-dimensional Unsteady Convection-dominated Diffusion Equations
Kim Yon-chol, Yun Nam and Chai Dong-ho
(Institute of Mathematics,Academy of Sciences of DPR Korea,Pyongyang,DPR Korea)
Communicated by Ma Fu-ming
Abstract:In this paper,a nearly analytic discretization method for one-dimensional linear unsteady convection-dominated diffusion equations and viscous Burgers’equation as one of the nonlinear equation is considered.In the case of linear equations,we find the local truncation error of the scheme is O(τ 2+h4)and consider the stability analysis of the method on the basis of the classical von Neumann’s theory.In addition,the nearly analytic discretization method for the one-dimensional viscous Burgers’equation is also constructed.The numerical experiments are performed for several benchmark problems presented in some literatures to illustrate the theoretical results.Theoretical and numerical results show that our method is to be higher accurate and nonoscillatory and might be helpful particularly in computations for the unsteady convection-dominated diffusion problems.
Key words:convection-dominated diffusion equation,nearly analytic discretization method,analysis of the stability
1 Introduction
This paper is focused on numerical methods for convection-diffusion problems that represent mathematical models for a number of(physical)processes in fluid mechanics,astrophysics,meteorology,multiphase flow in oil reservoirs,polymer flow,financial modeling,and many other areas.Computing solutions of these problems is an important and challenging problem,especially in the convection dominated case,in which viscous layers are so thin that classical finite difference method or finite element method can cause severe numerical unstabilities.If an insufficient amount of physical diffusion is compensated by an excessive numerical viscosity,these methods are typically stable,but the resolution may be severely affected.At the same time,the use of dispersive schemes may cause spurious oscillations that may,in turn,trigger numerical instabilities.
A number of numerical methods for the convection-dominated diffusion equations are developed,where the leading numerical methods include stabilization method,characteristic method and discontinuous Galerkin method,adaptive mesh method(see[1]–[5]). In addition,the exponentially-fitted method is also constructed(see[6]). The main focus in these methods is to construct the method to be more accurate,high stability and uniform convergent for the diffusion parameter.
In this paper,we consider a nearly analytic discretization method(NADM)for the convection-dominated diffusion problems and viscous Burgers’equation.
The NADM was developed for the solution of the two types of the hyperbolic and the parabolic equations in 1991 by Kondoh[7]. The key idea behind the NADM is that the order of accuracy of the approximate solution of the partial equation can be increased if the numerical process is implemented by using the properties of the differential relations and solution of the equation as much as possible without direct discretization as finite difference or finite element method(see[7]–[9]).
In this paper,we construct the NADM with the local truncation error O(τ2+h4)and consider the stability analysis of the NADM by using von Neumann theory for the different values of singulary perturbed parameters in the case of the singulary perturbed linear convection-diffusion equations. In addition,we construct NADM for the viscous Burgers’equation.
We can observe the method is very suitable for all cases. In order to illustrate the efficiency of the proposed method,some numerical experiments are performed for linear problems and nonlinear problems such as Burgers’equation presented in the previous literatures.
The rest of this paper is as follows.
In Section 2,we construct the NADM for the one-dimensional linear convection-dominated diffusion equation and find the local truncation error is O(τ2+h4).
One of the major issues in development of numerical schemes used to solve the convectiondominated diffusion equation is stability. For the obtained explicit scheme,we make an amplification matrixAfrom von Neumann theory and find the relation between the space step h and time step τ for the stability.
Finally,a numerical scheme for the Burgers’equation is presented.
In Section 3,the numerical experiments for several benchmark problems in the previous literatures are implemented.
The obtained theoretical and numerical results demonstrate that the NADM has high accuracy and less numerical dispersion for the diffusion parameter and might be helpful particularly in computations for the convection-dominated diffusion equations.
2 NADM for Convection-dominated Diffusion Equation
In this section,we consider the following linear convection-diffusion equation
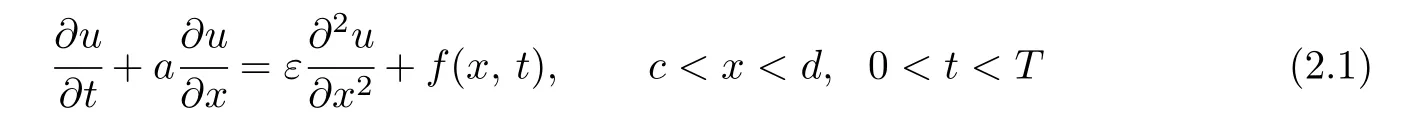
and viscous Burgers’equation(see[10])
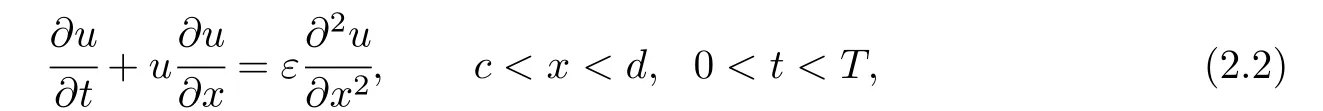
where 0<ε ≪1 is the diffusion parameter,a is constant.
For the above equations,the boundary and initial conditions are as follows:
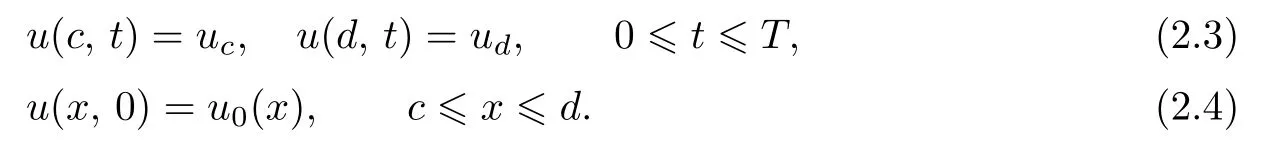
It is supposed that the solution of the solution(2.1)is sufficiently smooth. And for the simple discussion,we introduce the following representation:

2.1 NADM for Equation(2.1)
We express(2.1)and the relations obtained by the differentiation up to m-th for spatial variable x to(2.1)as follows:
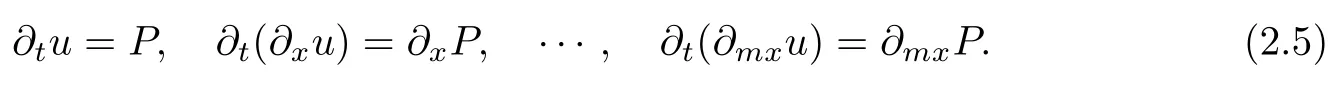
In order to increase the accuracy of the approximate solution,we solve the system of equation(2.5)including m+1 equations for the unknowns(see[7]).But,for the reason of complexity of numerical process,we implement the numerical method for only the case of m=1,namely,with equation(2.1)and ∂t(∂xu)=∂xP.
Let M and N be positive integers and Qh,τbe the set of grid nodes consisting of(xj,tn),where c=T.We set
Using the Taylor expansion for u,∂xu with respected to t in the vicinity of the node(xj,tn),we have
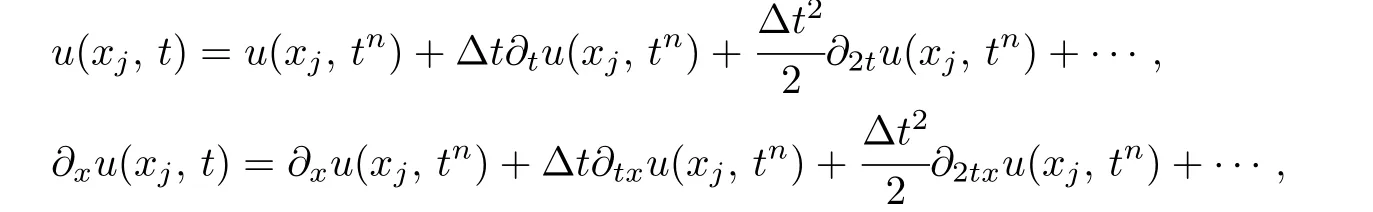
where ∆t=t −tn.From these expansions,we construct the following numerical schemes:
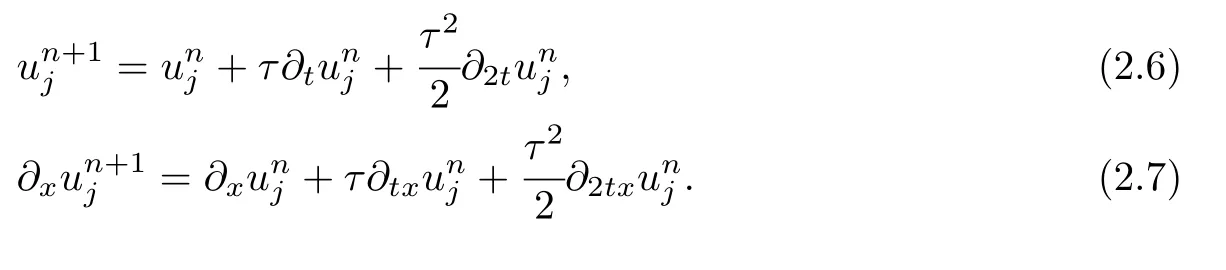
Meanwhile,the following relations are obtained from(2.1)and(2.5):

Then,in order to approximate ∂2xu,∂3xu,∂4xu,∂5xu in expressions(2.8)–(2.11),we use the
Taylor expansion presented in[7].Introducing the Taylor expansion function around xj,

where s=x −xjand considering the connection relations
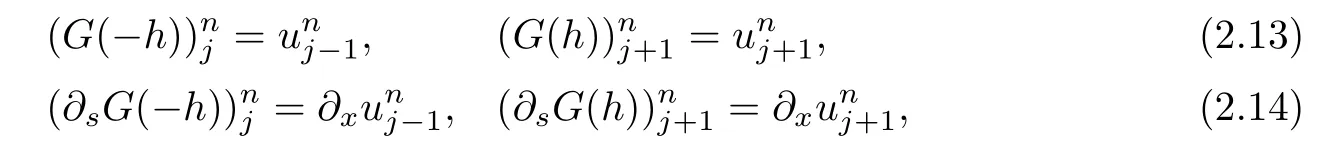
and calculating the values of ∂2xu,∂3xu,∂4xu,∂5xu at node(xj,tn)approximately from these expressions,we have

Putting(2.15)–(2.18)into(2.8)–(2.11),and then the obtained expressions into(2.6)–(2.7),we get the following numerical schemes for the solution of the equation(2.1):

By introducing Courant numberand diffusion numberand rearranging h schemes(2.19)and(2.20)in the standard form,we have

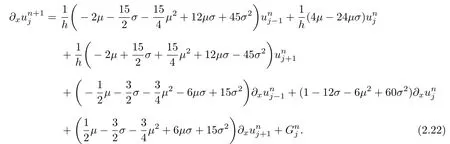
Here
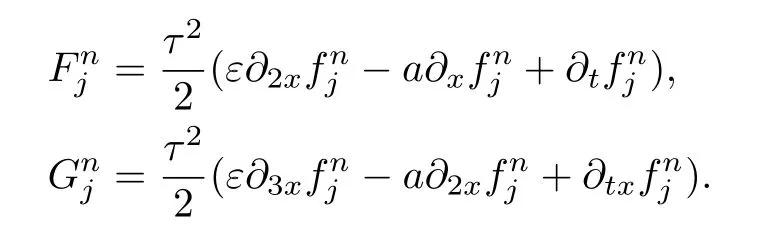
In general,by using the values of u0(x),we obtain the values of u0j,∂xu0jas follows:
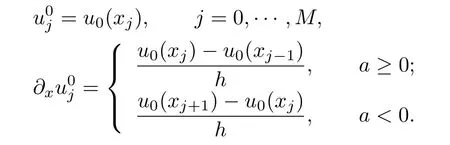
In the case of j=0,M,we use boundary condition(2.4)forand.
Meanwhile,we treat the boundary values ofandin following the method of[6].

Then,we have the following theorem on the local truncation error of the schemes(2.19)and(2.20):
Theorem 2.1Let us assume the solution u of the equations(2.1),(2.3)and(2.4)to be sufficiently smooth. Then,the local truncation error of the schemes(2.19)and(2.20)is O(τ2+h4),respectively.
Proof. From the approximate schemes(2.15)–(2.18)for ∂2xu,∂3xu,∂4xu,∂5xu,we have the following evaluations:
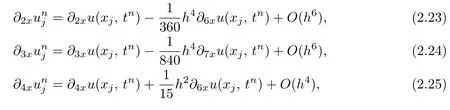
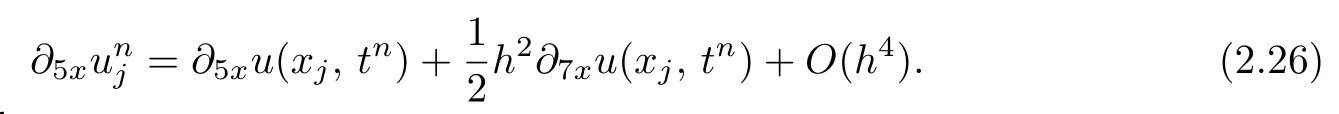
Let estimate the local truncation error of the scheme(2.17). For this,we introduce the following notification from(2.19),
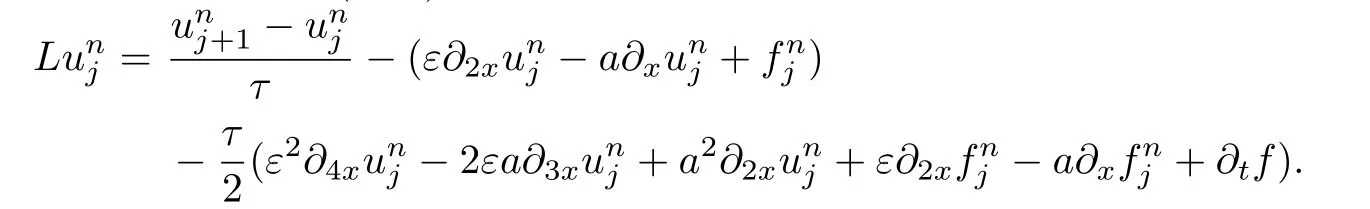
By using(2.8),(2.9)and(2.23)–(2.26),we have
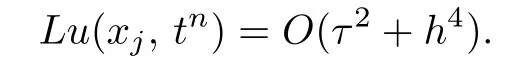
Namely,the local truncation error of the scheme(2.19)or(2.21)is O(τ2+h4).
Also,introducing the notification from(2.20),we have
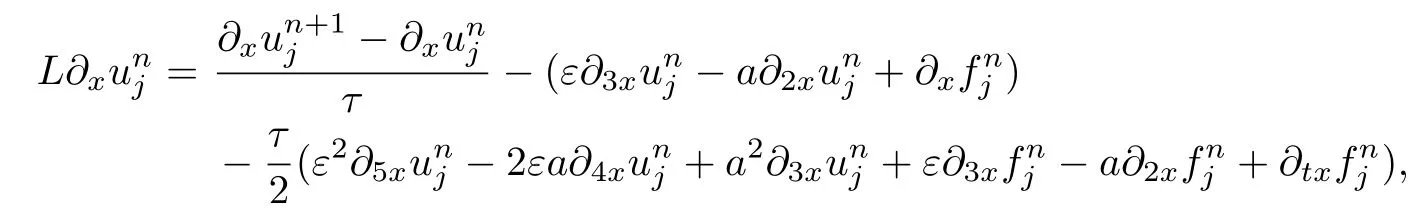
and using(2.10),(2.11),(2.23)–(2.26),we have
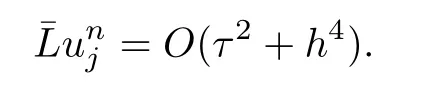
This completes the proof.
For the analysis of the stability,let

be the trial solution of the schemes(2.19),(2.20)or(2.21),(2.22),where
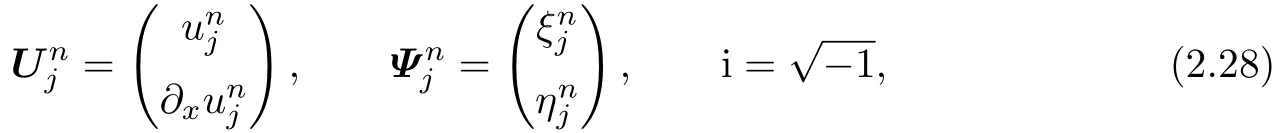
and k is the wave number.Then there would be the following relation betweenand,

whereAkis a two-dimensional amplification matrix and Bkis a two-dimensional vector in relation to f.From(2.15)–(2.18),we have
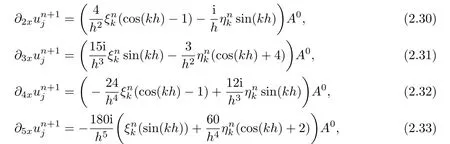
where A0=eikjh.
From relations(2.21),(2.22)and(2.30)–(2.33),we have(2.29).Then the elements of the matrixAkare as follows:
A11=a11+ib11, A12=a12+ib12, A21=a21+ib21, A22=a22+ib22,
where
a11=1 −4σ −2µ2+12σ2+(4σ+2µ2−12σ2)cos(kh),

Therefore,we have the von Neumann condition from the relation(4.6.5)of[12].For a given parameter ε,the spectral radius of the amplification matrix satisfies as τ →0 for all,where ρ(Ak)is the spectral radius of the amplification matrix Akand C is a constant independent of τ,h.

(2.34)is necessary but not sufficient for stability independent of the choice of norm(see[9]and[11]).If the necessary spectral criterion for stability is not satisfied,the problem is hopelessly unstable,and the situation cannot be corrected by any reasonable choice of norms(see[11]).In practice,in order to test for stability of the scheme,one computes eigenvalues of the amplification matrix and checks the von Neumann condition. If it is satisfied,the method is often stable,but sometimes it is not.These instabilities occur more often in the boundary conditions or nonlinearities than the von Neumann condition(see[9]).
In order to consider the stability of NADM for different values of parameter ε,it needs to explain the spectral radius of the amplification matrixAkin more detail.The eigenvalues λ ofAkare the root of the following complex quadratic equation:Introducing notifications

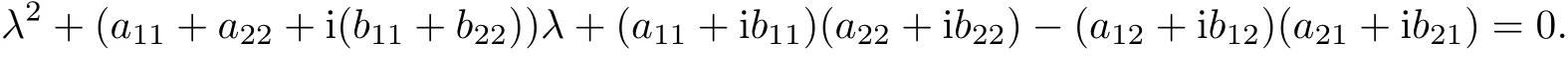
we have
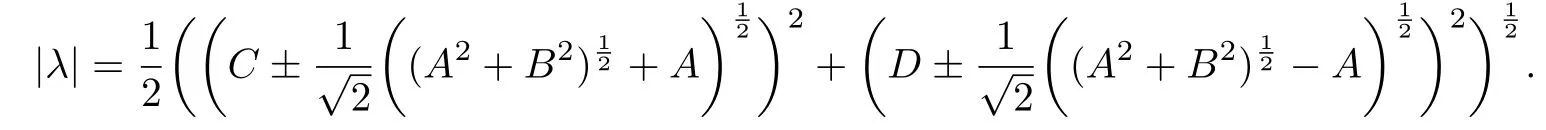
Therefore,we can know the following fact.
Corollary 2.1For a given parameter ε,von Neumann condition is as follows:
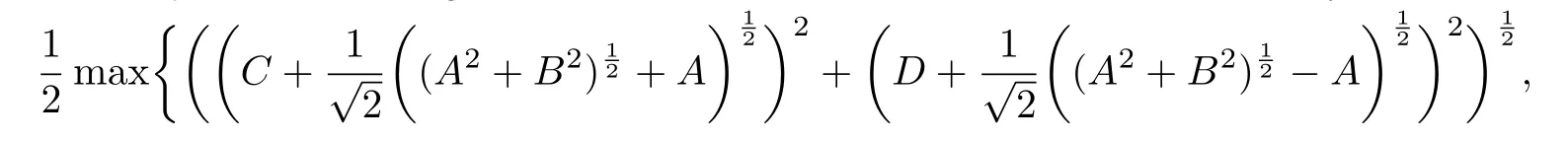
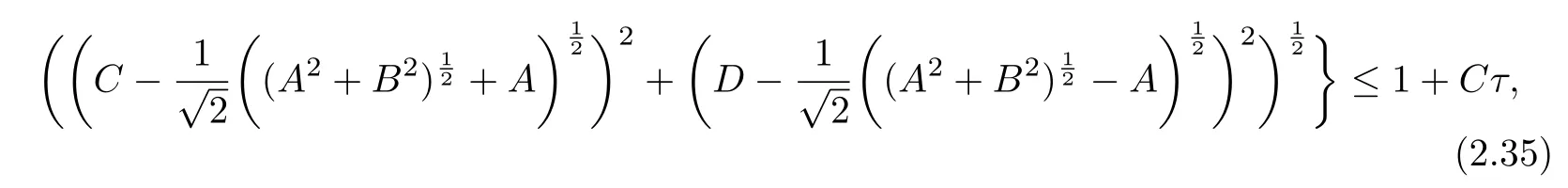
On the bases of the stability criteria(2.35),we show the relationship between time step τ and h for the parameter ε=1e 6,1e5,1e4,1e3,1e2,1e1,1 in Fig.2.1,where the constant C is fixed as 1.As− shown− in Fig.−2.1,th−e ratiois th−e smallest in the case of ϵ=1,namely,≈0.01.The ratios in the case of ϵ=1e −2,1e −3 are bigger than other cases and the profiles of the curves with ϵ ≤1e−5 are very similar.From the consideration of stability,we can expect that NADM is more suitable for the convection-dominated diffusion equations because the ratiosin the case of ε=1e −6,1e −5,1e −4,1e −3,1e −2 are much more than that in the case of ε=1e −1,1. We obtained similar results for other values of the parameter ϵ.

Fig.2.1 The relation τ and h for ε=1e −6,1e −5,1e −4,1e −3,1e −2,1e −1,1 based on(2.35)
It is verified in the numerical experiments that the criteria(2.35)becomes the sufficient condition for the stability.
Therefore,from Theorem 2.1,Corollary 2.1 and Lax’s equivalence theorem(see[12]),we have
Corollary 2.2For a given parameter ε,if τ and h are selected so that the criteria(2.35)is satisfied,then for such τ,h the approximate solutions obtained from the scheme(2.19),(2.20)or(2.21),(2.22)converge to the solution u of the equations(2.1),(2.3),(2.4)and ∂xu with the order of accuracy O(τ2+h4).
2.2 NADM for Burgers’Equation(2.2)
The construction of NADM for the Burgers’equation(2.2)is similar to the method for linear equation.The difference is to be the unknown u in the place of constant a.Therefore,the scheme becomes more complicated because of nonlinearity.From the equation(2.2)and(2.5),we have the similar relations to(2.8)–(2.11):
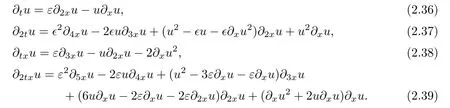
Substituting equations(2.36)–(2.39)into(2.6)and(2.7),we obtain the following the nonlinear numerical schemes:
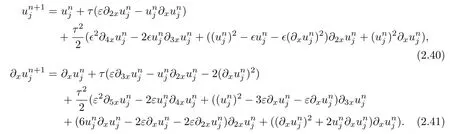
3 Numerical Experiments
In this section,we illustrate the efficiency of NADM by testing them with the examples based on convection-dominated diffusion equation(2.1)and Burgers’equation(2.2)presented in the paper(see[10]).
All of the computations of examples were implemented using VC++and MATLAB 2013a under Win7-x86-64.
For simplicity,we evaluate the error only for u.Here we use the discrete maximum norm
Example 3.1In this example,we test the sufficiency of the stability criteria(2.35)and efficiency for the test problem presented in paper[10],
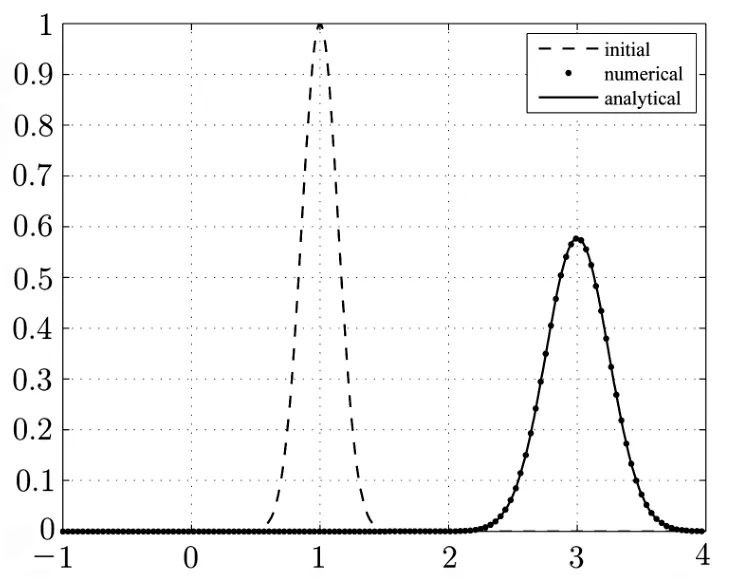
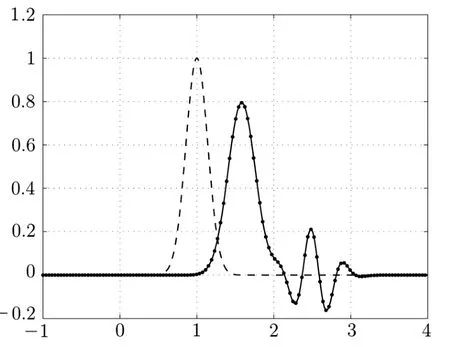
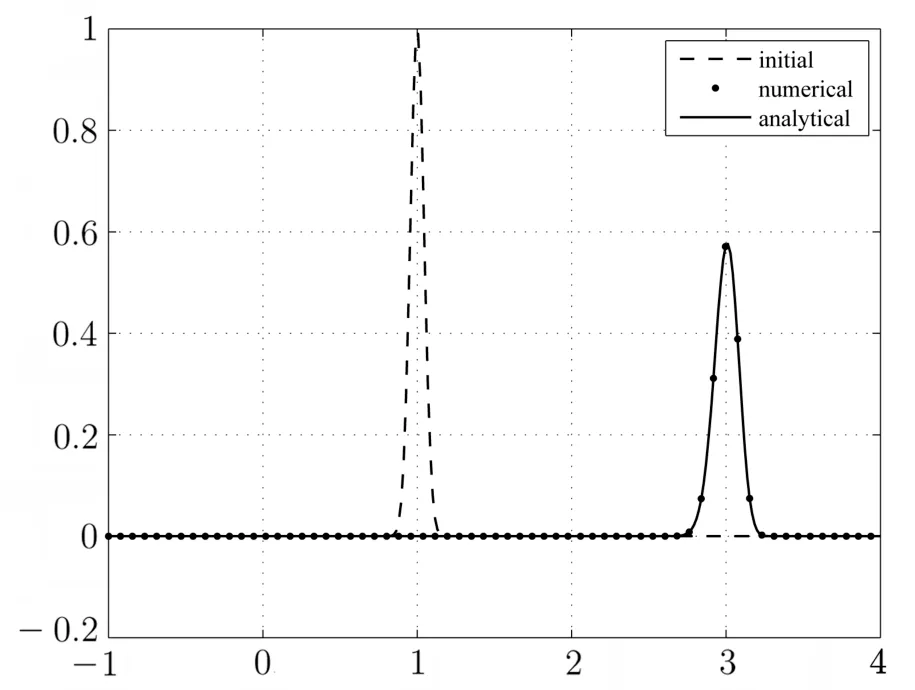
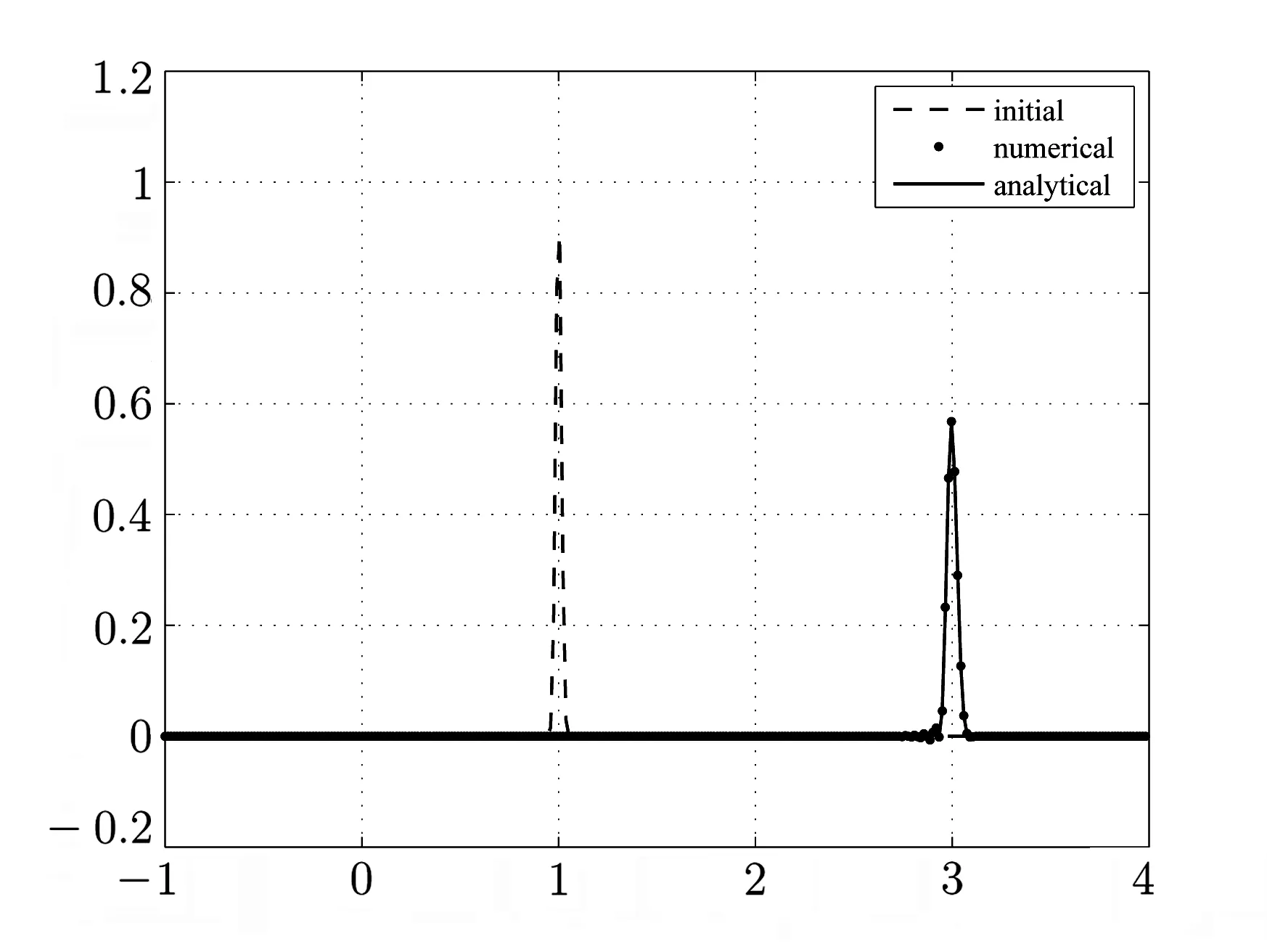
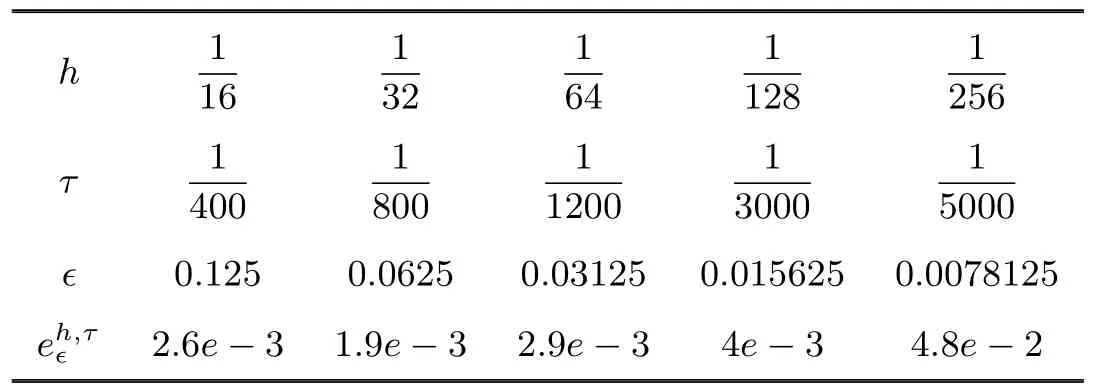
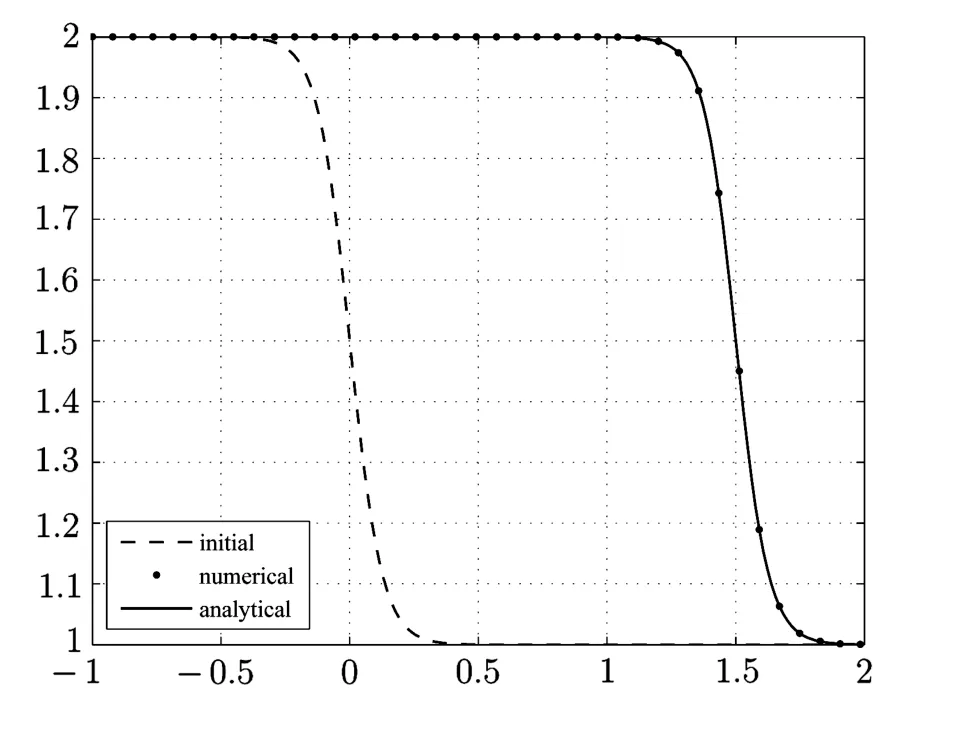
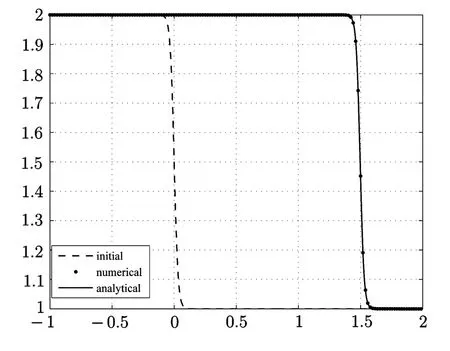
∂tu+a∂xu=ε∂2xu, −1 with the analytical solution This example is performed with a=1.Firstly,we verify numerically that criteria(2.35)is sufficient condition for the stability for a given different values of τ and h. Because NADM is the explicit scheme,it is required to choose proper τ for a fixed h so that the stability of the scheme should be satisfied.So we choose the proper τ from(2.35)fixing h for different values of the parameter ϵ.In order to confirm the validity of the criteria(2.35)numerically,we test for the case of ϵ=1e −2,1e −3. By using(2.35),the obtained results for τ and h are presented in the Table 3.1. Table 3.1 The values of h and τ for ϵ=1e −2,1e −3 First,we perform the testing for ϵ=0.01 and h=and show the result in Fig.3.1 and Fig. 3.2. We choose τ=from the Table 3.1. In the case of τ=,,the stable solution is obtained by the time T=2(see Fig.3.1).But,in the case of τ=,,the stability is destructed at T=0.58(see Fig.3.2). Fig.3.1 The solution at T=2 for τ=, in the case of ϵ=1e −2 Fig.3.2 The solution at T=0.58 for τ=,h= in the case of ϵ=1e −2 Also,the testing for ϵ=1e −3 is performed.In this case,we choose τ=, h=and the stable solution is obtained by the time T=2(see Fig. 3.3). But,in the case of τ=, the unstable oscillatory occurs at T=0.6(see Fig.3.4). Fig.3.3 The solution at T=2 for τ=,h=in the case of ϵ=1e −3 Fig.3.4 The solution at T=0.6 for τ=,h= in the case of ϵ=1e −3 We performed the testing and obtained similar results for other values of ϵ,τ,h. Next,the efficiency of NADM to solve the convection-dominated diffusion problems is confirmed through the discrete maximum norm for the numerical results.The convergence rates P h,τ(h)ϵ are computed by where τ(h)is taken from the criteria(2.35)(see Table 3.1). The numerical results for ϵ=1e −2,1e −3 are presented in Table 3.2. Table 3.2 The error and convergence rate for ϵ=1e −2,1e −3 For the comparison to the numerical results in the paper[10],we choose h=,α=1 among the parameters presented in the Example 4 of the paper,because this is the case that the parameter is the smallest,that is,ϵ=7.81251e −3 and ϵµ=0.18.In this case,we obtain=8.3e −4. Fig.3.5 The solution for τ=,h= in the case of ϵ=1e −4 We can observe that the structures of the numerical solutions are perfect and the scheme has a good behavior with higher order of accuracy if the stability of scheme is satisfied through numerical results. Example 3.2In this example,we consider the viscous Burgers’equation(2.2)presented in Example 5 of the paper[1],where The analytic solution of this problem is where a=1.5, c=0.5, ε=h(a+c). The viscous Burgers’equation is the simplest nonlinear model equation representing phenomena described by a balance between convection and diffusion.Moreover,the problem has a considerable interest from a numerical point of view because the Burgers’equation has the same convective and dissipative form as appears in many of fluid dynamic governing equations and has readily evaluated exact solutions for many combinations of initial and boundary conditions. In general,von Neumann theory for the stability cannot be applicable to the Burgers’equation because its nonlinearity,but we choose the proper time step τ fixing space step h on the basis of the criteria(2.35). The errors for the various values of h,τ and ϵ are presented in the Table 3.3. Table 3.3 The errors of the numerical results for the various values of h,τ and ϵ Fig.3.6 and Fig.3.7 show the numerical results at T=1 for h=,ϵ=0.03125 and h=,ϵ=0.0078125,respectively. Fig.3.6 The analytical solution and numerical solution at T=1 in the case of ε=0.03125 As shown in the table and figures,we can observe that the accurate and nonoscillatory numerical solution is obtained for the small parameter ϵ. Through this example,we can see the NADM to be applied to the nonlinear problems. Fig.3.7 The analytical solution and numerical solution at T=1 in the case of ε=0.0078125 In this paper,we proposed the NADM for the one-dimensional convection-dominated diffusion equations and Burgers’equation. We found the local truncation error of the NADM is O(τ2+h4)and carried out the stability analysis in the case of the linear problem.The obtained numerical results for several benchmark problems show that the NADM is to be effective and might be helpful particularly in computations for the convection-dominated diffusion equations.Unfortunately,the stability criteria of the method is relatively complicated.It needs to be further improved in the future.

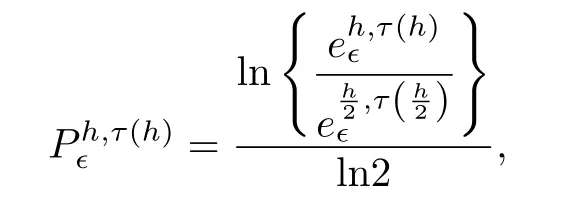

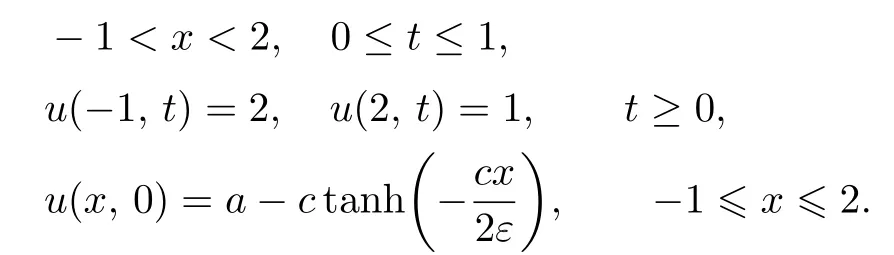

4 Final Remarks
 Communications in Mathematical Research2019年3期
Communications in Mathematical Research2019年3期
- Communications in Mathematical Research的其它文章
- Multiple Positive Solutions to Singular Fractional Differential System with Riemann-Stieltjes Integral Boundary Condition
- Planar Cubic G1 Hermite Interpolant with Minimal Quadratic Oscillation in Average
- An SIRS Epidemic Model with Pulse Vaccination,Birth Pulse and Logistic Death Rate
- The Transfer Ideal under the Action of a Nonmetacyclic Group in the Modular Case
- Fekete-SzegInequality for a Subclass of Bi-univalent Functions Associated with Hohlov Operator and Quasi-subordination
- Further Results on Meromorphic Functions and Their nth Order Exact Differences with Three Shared Values
