Planar Cubic G1 Hermite Interpolant with Minimal Quadratic Oscillation in Average

Li Jun-cheng

(College of Mathematics and Finance,Hunan University of Humanities,Science and Technology,Loudi,Hunan,417000)

Communicated by Ma Fu-ming

Abstract:In this paper we apply a new method to choose suitable free parameters of the planar cubic G1 Hermite interpolant.The method provides the cubic G1 Hermite interpolant with minimal quadratic oscillation in average. We can use the method to construct the optimal shape-preserving interpolant.Some numerical examples are presented to illustrate the effectiveness of the method.

Key words:cubic Hermite interpolant,free parameter optimization,shape-preserving interpolant

1 Introduction

As we know,the planar cubic Hermite interpolant includes two cases of C1continuity and G1continuity.The cubic C1Hermite interpolant can be described as follows:where i=and pi+1are two end points together with two tangent vectors mi and mi+1,

are cubic Bernstein polynomials. The cubic G1Hermite interpolant can be described as follows:wherediand di+1are unit tangent directions of the two end points,αi,0and αi,1are positive numbers.

For the cubic C1Hermite interpolant expressed in(1.1),the tangent vectorsmi,mi+1are generally required to be given in advance.But in practical applications the tangent vectors are rarely available. In most cases,minimization an appropriate functional is applied to determine the tangent vectors. As it was proposed in[1]and[2],one can determine the tangent vectors by minimizing

Different to(1.3),in[3]and[4],the method was presented by minimizing

where

L(t):=Li(t)=(1 −t)pi+tpi+1.

Particularly,the method by minimizing I0expressed in(1.4)provides the interpolant with minimal quadratic oscillation in average,and the method by minimizing I1expressed in(1.4)provides the interpolant with minimal derivative oscillation.

For the cubic G1Hermite interpolant in(1.2),the unit tangent directionsdi,di+1are generally given while the numbers αi,0and αi,1are usually used as free parameters. Although there are several approaches to choose suitable free parameters,the common ways to determine the free parameters are achieved by minimizing Jkthat have been applied to the cubic C1Hermite interpolant.In particular,the method by minimizing J2provides the interpolant with minimal strain energy(see[5]and[6]),and the method by minimizing J3provides the interpolant with minimal curvature variation(see[7]–[9]).

A natural idea arises:maybe we can use the methods by minimizing Ikto choose the parameters αi,0and αi,1for the cubic G1Hermite interpolant,since the methods have been applied to the cubic C1Hermite interpolant. With this in mind,we consider here the problem of determining the parameters αi,0and αi,1by minimizing I0that provides the cubic C1Hermite interpolant with minimal quadratic oscillation in average. Because the piecewise linear interpolantL(t)is the simplest shape-preserving interpolant,the cubic Hermite interpolant obtained by minimizing I0is almost flat-shaped. This means we can use the method by minimizing I0to construct the optimal shape-preserving interpolant.

The remainder of this paper is organized as follows.We present the computing method for determining the parameters αi,0and αi,1by minimizing I0in Section 2. In Section 3 we show some numerical examples in comparison with the method of curvature variation minimization.

2 The Computing Method

Because the cubic G1Hermite interpolant can be studied locally,we only need to consider a piece of curve bi(t).According to(1.4),the quadratic oscillation in average of bi(t)can

be expressed as follows:

By computing,we have

where ∆pi:=pi+1−pidenotes the line segment from pito pi+1,a·b:=axbx+aybydenotes the dot product of planar vector.Since w

e can rewrite(2.1)as follows:

By(2.2),we have

Let φi:=∠(di,di+1),where ∠(a,b)represents the angle between vectors a and b.

Then the determinant

Therefore,according to(2.3)and(2.4),the following unique global minimum of functional

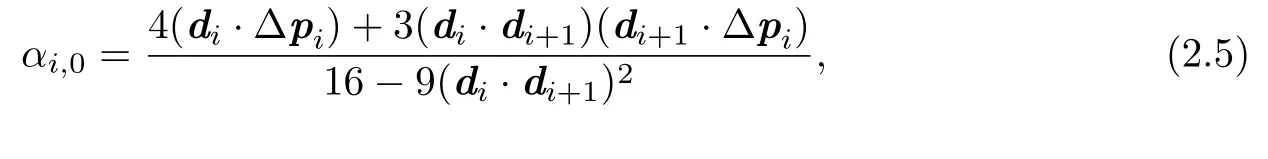
3 Numerical Examples and Comparisons

We compare the proposed method with the method of curvature variation minimization(see[8]and[9]).As it was proposed in[8]and[9],the unique parameters of the cubic G1Hermite interpolant with minimal curvature variation can be given by

where a×b:=axby−bxaydenotes the planar vector product.

The first example we consider a piece of curve.Given the following date,

p0=(−1,0), p1=(1,0), d0=(cos θ0,sin θ0),

d1=(cos θ1,−sin θ1), θ0=, θ1=.

The values of the parameters of the two methods calculated by(2.5),(2.6)and(3.1),(3.2)are shown in Table 3.1.

Table 3.1 The values of the parameters of the two methods(a piece of curve)

In Fig.3.1 we represent the graphs of the following curves:the cubic Hermite interpolant with minimal curvature variation(in thick line),the cubic Hermite interpolant with minimal quadratic oscillation in average(in leptonema),and the polygonal line joining the points pi(i=0,1)(in dotted).

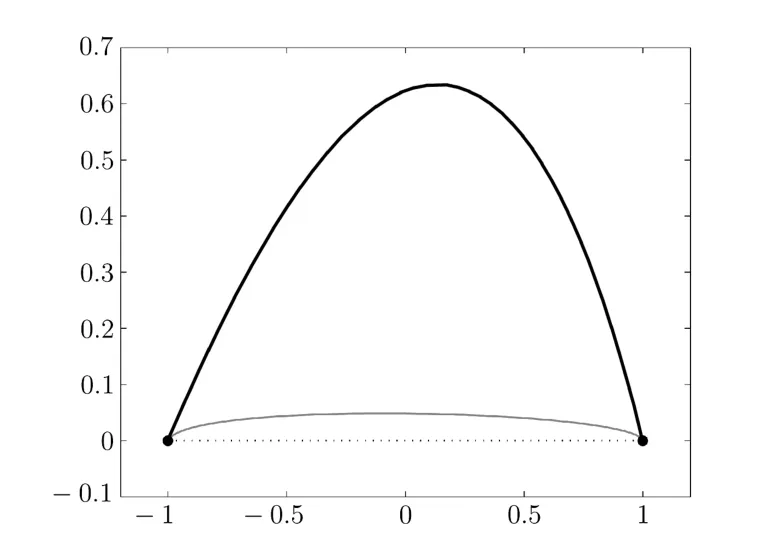
Fig.3.1 The graphs of the curves(a piece of curve)

The second example is to consider a composite curve.Given the following date,

p0=(0,0), p1=(3,1), p2=(5,2),

p3=(6,4), p4=(8,5), p5=(11,6),

d0=(cos θ0,sin θ0), d1=(cos θ1,sin θ1), d2=(cos θ2,sin θ2),

d3=(cos θ3,sin θ3), d4=(cos θ4,sin θ4), d5=(cos θ5,sin θ5),

θ0=, θ1=, θ2=,

θ3=, θ4=, θ5=.

The values of the parameters of the two methods calculated by(2.5),(2.6)and(3.1),(3.2)are shown in Table 3.2.

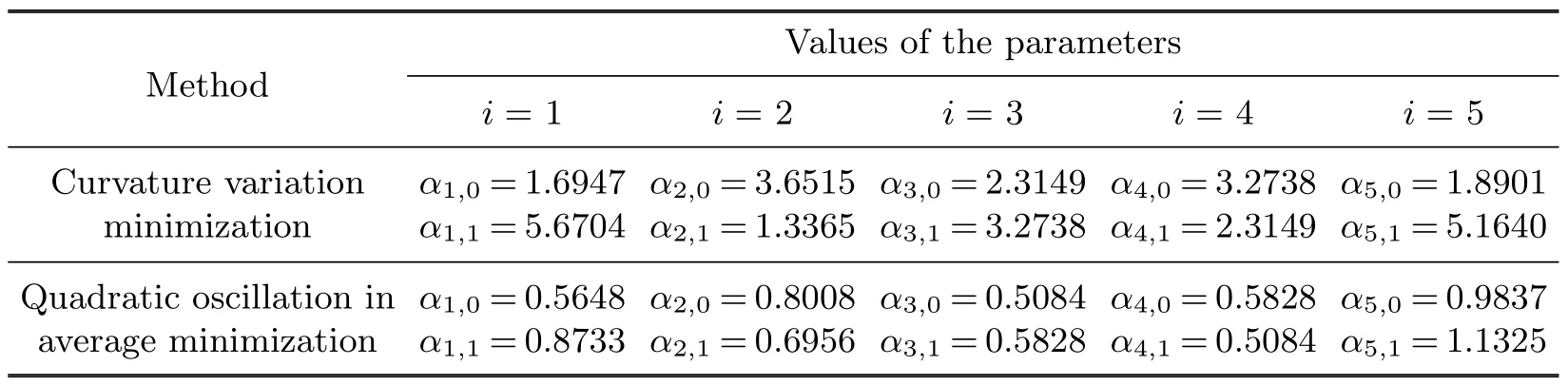
Table 3.2 The values of the parameters of the two methods(a composite curve)

Fig.3.2 shows the cubic Hermite interpolant with minimal curvature variation(in thick line),the cubic Hermite interpolant with minimal quadratic oscillation in average(in leptonema),and the polygonal line joining the points pi(i=0,1,···,5)(in dotted).

Fig.3.2 The graphs of the curves(a composite curve)

Fig.3.1 and Fig.3.2 show that the cubic Hermite interpolant with minimal quadratic oscillation in average is nearer to the polygonal line than the cubic Hermite interpolant with minimal curvature variation.Since the polygonal line is the simplest shape-preserving interpolant,the cubic Hermite interpolant with minimal quadratic oscillation in average provides the optimal shape-preserving interpolant.

The last example let us consider the following data taken from a unit semicircle:

p0=(cos 0,sin 0), p1=(cos,sin), p2=(cos,sin),

p3=(cos,sin), p4=(cos,sin), p5=(cos,sin),

p6=(cos,sin), p7=(cos π,sin π),

d0=(−sin 0,cos 0), d1=(−sin,cos), d2=(−sin,cos),

d3=(−sin,cos), d4=(−sin,cos), d5=(−sin,cos),

d6=(−sin,cos), d7=(−sin π,cos π).

In Fig.3.3 we represent the graphs of the following curves:the cubic Hermite interpolant with minimal curvature variation(in thick line),the cubic Hermite interpolant with minimal quadratic oscillation in average(in leptonema),and the unit semicircle(in dotted).

Fig.3.3 Interpolating a unit semicircle

Fig.3.3 shows that the cubic Hermite interpolant with minimal quadratic oscillation in average is better when interpolating a unit semicircle,since the cubic Hermite interpolant with minimal curvature variation is self intersection at the beginning and end of the curve.