An SIRS Epidemic Model with Pulse Vaccination,Birth Pulse and Logistic Death Rate
Gao Jian-zhong and Zhang Tai-lei
(School of Science,Chang’an University,Xi’an,710064)
Communicated by Li Yong
Abstract: In this paper,we propose an SIRS epidemic model with pulse vaccination,birth pulse and Logistic death rate.By using the stroboscopic map of a discrete dynamical system,the disease-free periodic solution(DFPS for short)of the model under pulse vaccination and birth pulse is obtained.Based on the Floquet theory and comparison theorem of impulsive differential equations,the global asymptotic stability of the DFPS is given,and sufficient conditions for the permanence of the model are obtained.In addition,numerical simulations are done to confirm our theoretical results.
Key words: Logistic death rate,birth pulse,threshold value,global stability,permanence
1 Introduction
Infectious diseases have tremendous influence on human life.Every year,millions of people died of various infectious diseases.Controlling infectious diseases have been an increasingly complex issue in recent year.Pulse vaccination has been testified to be an effective strategy in preventing such viral infectious as rabies,yellow fever,polio virus,encephalitis B.For many epidemic models,we always assume that the population birth rate is either a constant or proportional to the number of population.In short,it is assumed that the population is always born at all times. Generally speaking,this assumption is not reasonable for those large number of individuals and population with overlapping generations.For some animals,especially some sea animals,these animals usually produce offspring in the special months of year.In other words,the birth rate is not a continuous function of time,but appears in the form of pulse.In addition,in order to control the epidemic of infectious diseases,some vaccines are often carried out in a certain time every year,which is also a form of pulse.On the basis of facts,Ma et al.[1]discussed a model with birth pulse,and assumed that the birth rate is constant.In[2]–[5],the authors hypothesized that the birth rate and the mortality rate are density dependent and assumed that population is born in the form of pulse.On the basis of those assumptions,the conditions of equilibrium points stability were given. In[6]–[11],the authors analyzed that pulse vaccination has influence on control of infectious disease.Han and Wei[12]studied a delay SEIR epidemic model with birth pulse,pulse vaccination and vertical infection,obtained two thresholds and analyzed the stability of the model. In[13]and[14],the authors discussed the branch questions of the model with birth pulse and pulse vaccination.In[12],the authors vaccinated all newborns.Here,only pulse vaccination is given to susceptible people in this paper.We establish that pulse vaccination and birth pulse occur at the same time and consider vertical infection.This is different from[13]and[14].In short,in this paper,based on the previous articles[12]–[14],we consider the birth pulse and pulse vaccination at the same time,and we assume that the disease has vertical infection and mortality due to disease,we establish compartment model and analyze existence of the DFPS,we further discuss stability and permanence of disease.
The organization of this paper is as follows:In Section 1,we establish an SIRS epidemic model. In Section 2,by using the stroboscopic map of a discrete dynamical system,we analyze existence of the DFPS and deal with the global attractivity of the DFPS.In Section 3,we discuss the permanence of model.In Section 4,we do numerical simulations to confirm our theoretical results.Finally,we make a summary for this article.
2 Model Description
In order to describe the model,S(t),I(t)and R(t)represent the number of the susceptible,the infected and the recovered at time t,respectively.The total population number at time t is expressed by
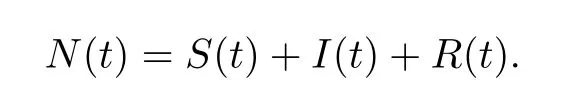
Main assumptions are as follows:
(i)µN(t)is exponential immigrant for the susceptible.
(ii)Adopting Logistic death rate d+(see[15]–[17]),d is the natural death rate and K is the environmental capacity.
(iii)Adopting standard incidence rate.
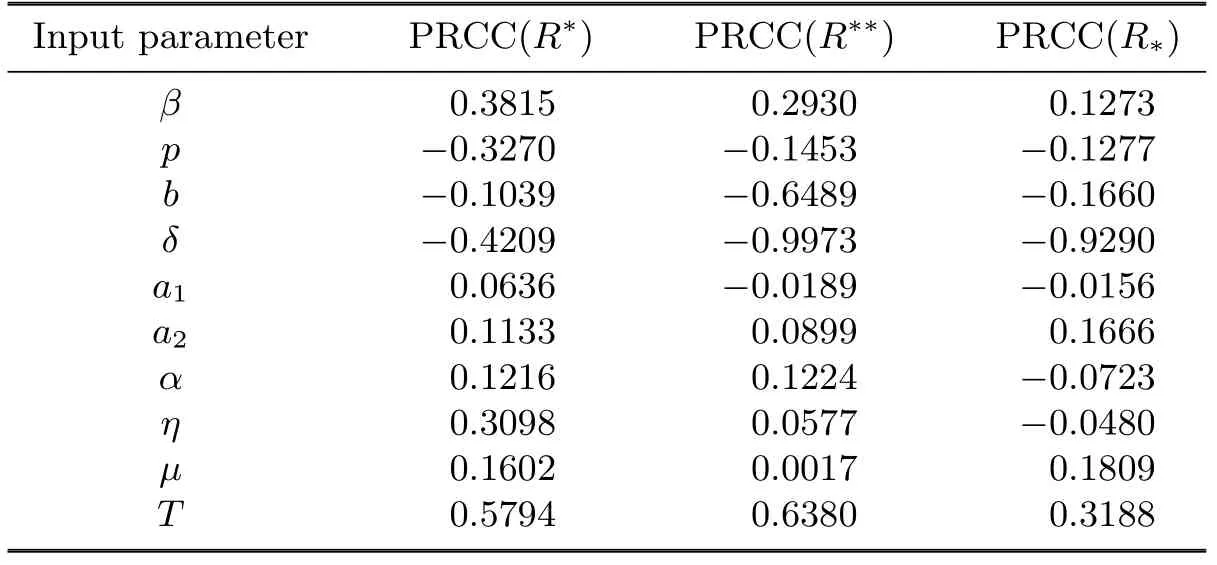
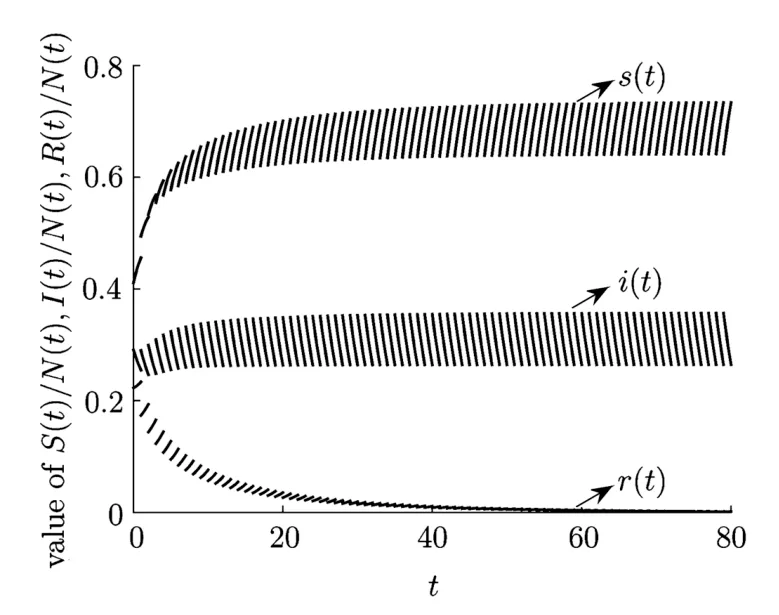
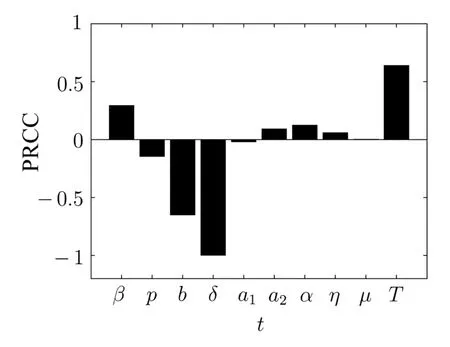
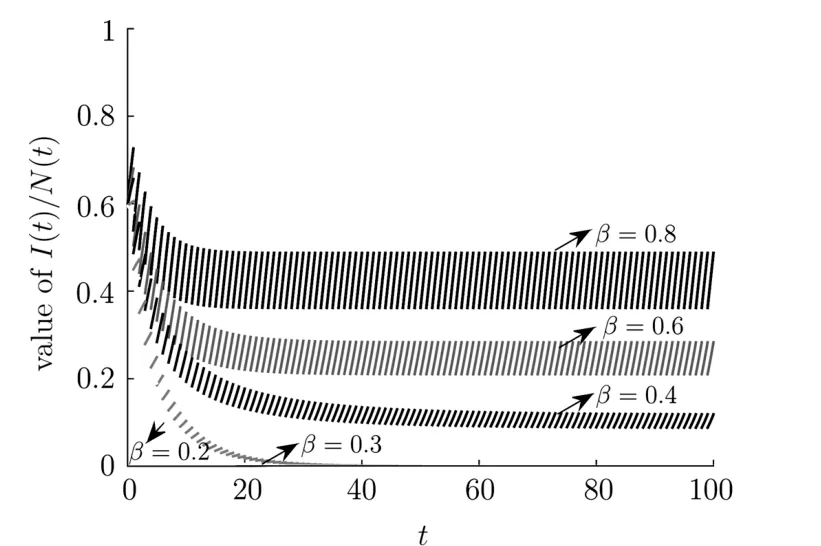
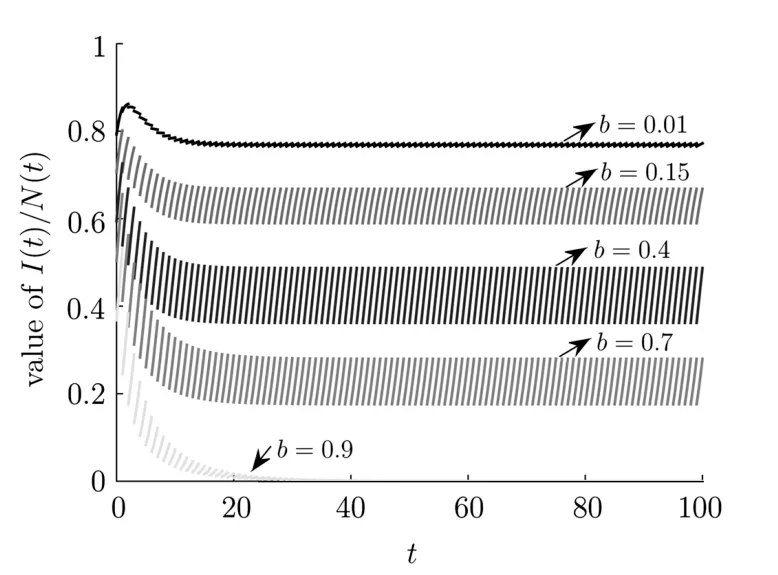
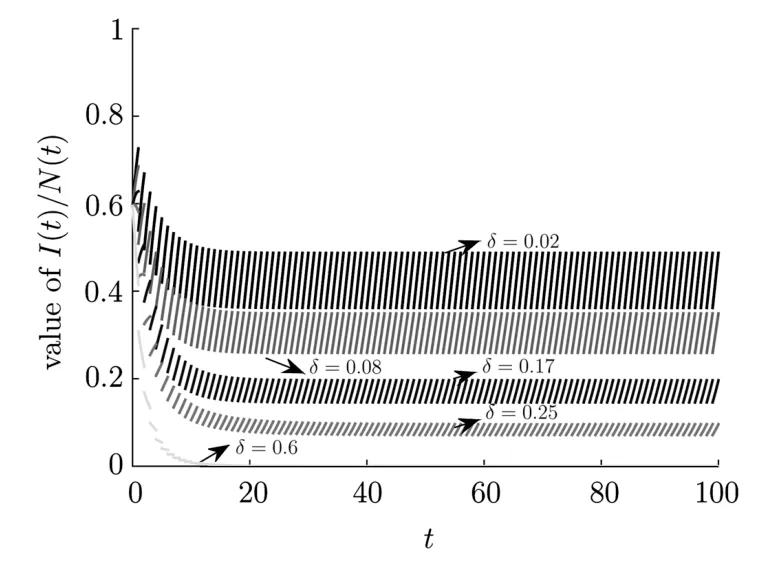
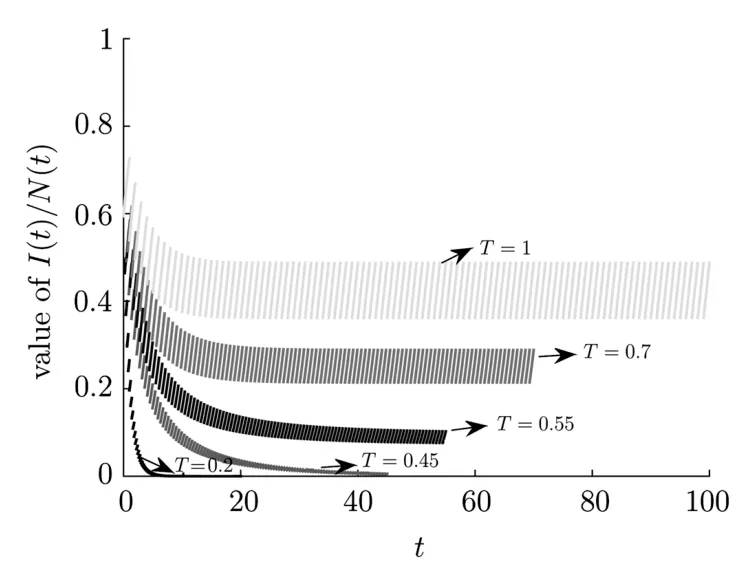
(iv)p(0 (v)β is average number of adequate contact rate of an infectious individuals per unit time.δ is the recovery rate of infectious individuals.α is the mortality induced disease for infectious individuals.η is the rate of losing immunity. (vi)b(b>0)is the birth pulse rate of population and newborns in susceptible class all enter into susceptible class but recovered newborns are not all immune,some enter into susceptible class(proportion is a1,0 With the above assumptions(i)–(vi),we can obtain an SIRS epidemic model with pulse vaccination,birth pulse and Logistic death rate: In model(2.1),total population N(t)=S(t)+I(t)+R(t)satisfies Obviously,N(t)is bounded above asµ>d(t →∞). Otherwise,N(t)→0 asµ nd s(t)+i(t)+r(t)=1.Then model(2.1)turns to The initial condition of model(2.2)is given as where The meaningful domain of the model(2.2)is D={(s,i,r)∈R3+:s+i+r=1}and it is easy to show that D is a positively invariant set. The solution of model(2.2)is a piecewise continuous functionis continuous on(kT,(k+1)T],k ∈N andexists. In fact,the right hand side of model(2.2)can ensure the existence and uniqueness of solutions of model(2.2). One of the most important questions in mathematical studies of epidemics is the possibility of the eradication of disease.In this section,we analyze the stability of the DFPS of model(2.2).The following lemmas will be used in the proof of our main results. Lemma 3.1Consider the following impulsive differential equation where 0<θ<1,and σ(t)>0 is a T-periodic function.We have the following results. Proof. For system(3.1),we consider piecewise integral.Integrating(3.1)on the interval(0,T],we have Integrating on the interval(T,2T],we have we repeat above process.Integrating on the interval(nT,(n+1)T],we have From this formula,we have u(t)→0(t →∞)when θexp<1,and u(t)→∞ Lemma 3.2Consider the following impulsive differential equation where a>0,b>0,d>0,v>0,0<ρ<1,0 which is globally asymptotically stable.Here Proof. By directly calculating,we obtain the solution of the first and second equations in system(3.2) Using the third and fourth equations of system(3.2),we can employ the stroboscopic map such that where It is easy to know that the maps f and g have unique positive fixed points,respectively, Obviously, Thus 0 Next,we demonstrate the existence of a disease-free solution,in which infectious individuals are entirely absent from the population permanently,i.e.,i(t)≡0 for all t ≥0.Under this condition,the growth of susceptible individuals and recovered individuals must satisfy the following impulsive differential system According to Lemma 3.2,we know that the periodic solution of system(3.3)is of form which is globally asymptotically stable,where Denote two quantities where Theorem 3.1If R∗<1,then the DFPS(s∗(t),0,r∗(t))of the model(2.2)is locally asymptotically stable in D. Proof. We discuss the local stability of the periodic solution(s∗(t),0,r∗(t)),which may be determined by considering the behavior of small amplitude perturbations of solutions. Define x(t)=s(t)−s∗(t),y(t)=i(t),z(t)=r(t)−r∗(t).Here x(t),y(t)and z(t)may be written as where the fundamental matrixΦ(t)satisfies andΦ(0)=EEEis the identity matrix.So where “∗”is not necessarily computed in detail as it is not required in the following analysis. The resetting impulsive conditions of model(2.2)become Hence,according to the Floquet theory,if the moduli of three eigenvalues of the matrixMMM=BBB(T)Φ(T) are less than one,then the periodic solution(s∗(t),0,r∗(t))is locally stable. Here,three eigenvalues of matrix MMM are λ1,λ2,λ3,respectively.In fact,It is obvious that 0<λ1<1,0<λ3<1.Thus,the stability of(s∗(t),0,r∗(t))is decided by whether λ2<1 or not.We conclude that the DFPS(s∗(t),0,r∗(t))is locally stable if that is, By simple calculation,we have which is valid due to R∗<1.Therefore,we can draw a conclusion from above analysis that if R∗<1 then the DFPS(s∗(t),0,r∗(t))of model(2.2)is locally asymptotically stable.This completes the proof of Theorem 3.1. Next,we prove the global attractivity of the DFPS(s∗(t),0,r∗(t))of model(2.2). Theorem 3.2If R∗∗<1,then the DFPS(s∗(t),0,r∗(t))of model(2.2)is global attraction. Proof. From the first and fourth equations of model(2.2),we have where W=max{a1,a2}.We consider the following impulsive comparison system According to Lemma 3.2,we know that periodic solution of system(3.4)is of form where Let(s(t),i(t),r(t))be an arbitrary solution of model(2.2)with initial value(2.3)and s(0+)=s0>0.There exists a positive number ε1sufficiently small and k1∈N such that s(t)≤x(t) According to the second and fifth equations of model(2.2),we can assert that for all t>k1T.According to Lemma 3.1,we have Since R∗∗<1,that is, We combine with limit system(3.3)of model(2.2).Therefore,s(t)→s∗(t),r(t)→r∗(t)as t →+∞. Thus we have proved global attractivity of the DFPS(s∗(t),0,r∗(t))of model(2.2).This completes the proof. Denote a quantity where Theorem 4.1If R∗>1,then the model(2.2)is permanent. Proof. Firstly,we prove that there exists an m1>0 such that i(t)≥m1as t sufficiently large.This part is divided into two steps. (1)Since R∗>1,there exist two positive numbersand ε2sufficiently small such that where where w=min a1,a2.We consider the following impulsive comparison system According to Lemma 3.2,we know that periodic solution of system(4.3)is of form There exists a k3>k2such that According to the second and fifth equations of model(2.2),we have for all t>k3T.Integrating system(4.5)on the interval(k3T,t],we have where[t]−1 Case 1. tqis an impulsive time.Write tq=k4T,(k4+n1)T<≤(k4+n)T for some n,we repeat above process(4.2)–(4.5)on the interval(tq,].Integrating system(4.5)on the interval(tq,],we have which implies Since R∗>1,then i(t)→∞as n →∞.That is,there exists an N∗>0 such that we have i()>1 for all n ≥N∗.This is a contradiction.Therefore,the length of interval(tq,]has a uniform upper bound which is denoted by−tq≤N1T. According to the second and fourth equations of model(2.2),we have where ρ=(δ+µ+α).Integrating system(4.6)on the interval(tq,(k4+N1)T],we have Since(tq,]⊆(tq,(k4+N1)T],then i(t)≥q1for t ∈(tq,]. Case 2. tqis not an impulsive time.Write k4T which implies Since R∗>1,then i(t)→∞as n →∞.That is,there exists an N∗∗>0 such that we have i()>1 for all n ≥N∗∗.This is a contradiction.Therefore,the length of interval[tq,]has a uniform upper bound which is denoted by−tq≤N2T. Integrating system(4.6)on the interval[tq,(k4+N2)T],we have Since[tq,]⊆[tq,(k4+N2)T],then i(t)≥q2for t ∈[tq,]. Set m1=min{q1,q2}.According to the above two cases,we conclude that Next,we prove that there exist two positive numbers m2,m3such that s(t)≥m2,r(t)≥m3as t sufficiently large.There exist two positive numbers ε3and ε4sufficiently small. From the first and fourth equations of model(2.2),we have where w=min{a1,a2}.We consider the following impulsive comparison system According to Lemma 3.2,we know that periodic solution of system(4.7)is of form where According to impulsive comparison principle,there exists a k5>k4such that From the third and sixth equations of model(2.2),we have we consider the following impulsive comparison system We know that periodic solution of system(4.9)is of form where According to impulsive comparison principle,there exists a k6>k5such that In view of(4.8)and(4.10),we have The proof is completed. In this section,some numerical results of system(2.2)are presented for supporting the analytic results obtained above. Parameter values in Table 5.1 are derived from[18]and[19]and partial rank correlation coefficients(PRCCs)(see[20])for R∗,R∗∗,R∗and each input parameter in Table 5.2. Table 5.1 Values of parameters Table 5.2 PRCCs for R∗,R∗∗,R∗and each input parameter We can get from the above Table 5.1 and Table 5.2 as follows: (1) T=1,p=0.3,µ=0.1,η=0.2,α=0.002,β=0.8,δ=0.2,a1=0.86,a2=0.9,b=0.4,then R∗=0.9231<1 and R∗∗=0.9713<1.According to Theorems 3.1 and 3.2,we know that the disease will disappear(see Fig. 5.1). Here we choose the initial values s(0)=0.3,i(0)=0.3,r(0)=0.3. (2)T=1,p=0.035,µ=0.1,η=0.2,α=0.002,β=0.8,δ=0.02,a1=0.32,a2=0.9,b=0.4,then R∗=1.7889>1,R∗∗=1.9505>1 and R∗=1.3920>1,we know that the disease will be permanent(see Fig.5.2).Here we choose the initial values s(0)=0.3,i(0)=0.3,r(0)=0.3. Fig.5.1 The global stability of the DFPS(2.2) Fig.5.2 The permanence of the model(2.2) (3)From Figs.5.3–5.5,it can be shown results for the PRCC and these results illustrate the dependence of thresholds R∗,R∗∗and R∗on each parameter. From the biological significance of the model,we only study the sensitivity of contact rate β,pulse vaccination p,birth pulse rate b,recovery rate δ and pulse vaccination period T on thresholds R∗,R∗∗and R∗. In Fig.5.6,this changes value of parameter β and other parameters values are the same as Fig.5.2. Fig.5.3 PRCCs results for the dependence of R∗on each parameter Fig.5.5 PRCCs results for the dependence of R∗on each parameter Fig.5.4 PRCCs results for the dependenceof R∗∗on each parameter Fig.5.6 This is the change in β In Fig.5.7,this changes value of parameter p and other parameters values are the same as Fig.5.2. In Fig.5.8,this changes value of parameter b and other parameters values are the same as Fig.5.2. Fig.5.7 This is the change in p Fig.5.8 This is the change in b In Fig.5.9,this changes value of parameter δ and other parameters values are the same as Fig.5.2. In Fig. 5.10,this changes value of parameter T and other parameters values are the same as Fig.5.2. Fig.5.9 This is the change in δ Fig.5.10 This is the change in T According to Figs.5.3–5.5 of the PRCC,we can get the dependence of the thresholds R∗,R∗∗,R∗on each parameter. The influence extent of each parameter is reflected by the absolute value of PRCC value(sample space N=1500).We can see that β and T have positive effect on the thresholds R∗,R∗∗,R∗,but p,b and δ have negative effect on the thresholds R∗,R∗∗,R∗.So we do sensitivity analysis of parameters and get Figs.5.6–5.10.The results are consistent with Figs.5.3–5.5. In real life,some strategies are given to control the infectious diseases in this model. (a)Because the susceptible people is easy to infect the diseases,we must do a good job of protective measures for the susceptible people.Generally,it is to reduce the contact between the susceptible people and the infected people as far as possible,which reduces the contact rate β,so this result can also be reflected from Fig.5.6. (b)For controlling the epidemic of infectious diseases,the cost of continuous vaccination is relatively high. Hence,we can choose pulse vaccination. Pulse vaccination can reduce cost,and it can enhance the success rate of pulse vaccination through pulse vaccination to control infectious diseases.From Fig.5.7,we can increase the pulse vaccination rate p to control the epidemic of the diseases,such as rabies and yellow fever. (c)In real life,there is vertical transmission of diseases(mother-to-child). Nowadays,the medical facilities of hospitals have been improved to a certain extent,so many people often have disease checks before marriage. If we detect that people have some kind of infectious disease from the outside or carried by themselves,we can treat these diseases through advanced medical equipment,so that the disease can be extinct,then people give birth to healthy children.That is to say,we can increase the birth rate b through scientific means to achieve the goal of diseases extinction(see Fig.5.8). (d)With the development of society,the medical facilities of hospitals have been improved to a certain extent,the cure rate has been improved,so that the infected people can get better treatment,that is,we can enhance the cure rate δ to control the spread of infectious diseases.This result can be reflected in Fig.5.9. (e)Pulse vaccination is carried out at a fixed time point,so we can reduce the time interval,that is,we can short the cycle T to control the spread of disease,which can also be reflected in Fig.5.10. Therefore,in order to reduce and control the spread of the infectious disease,we can increase pulse vaccination rate p,birth pulse rate b,recovery rate δ and decrease contact rate β,pulse vaccination period T by scientific means from the above analysis(see Figs.5.6–5.10). The innovation of this paper is that pulse vaccination,birth pulse and vertical transmission are introduced into SIRS epidemic model,and some important properties are obtained. Three critical values are obtained in this paper(see Theorems 3.1,3.2 and 4.1).If max{R∗, R∗∗}<1,then disease will be extinct. If R∗>1,then the disease will be permanent.In addition,it can be shown that the PRCC results illustrate the dependence of R∗,R∗∗and R∗on each parameter in Figs.5.3–5.5.Therefore,we can get a conclusion that increasing pulse vaccination rate p,recovery rate δ,birth pulse b and decreasing contact rate β,pulse vaccination period T can control the spread of the infectious disease(see Figs.5.6–5.10).What’s more,we can raise the level of medical care,increase the rate of cure,and make the infected individuals recover from the disease as soon as possible. In real life,there is a certain seasonality for the reproductive offspring of special species,such as marine animals and parasitic organisms.The birth rate of this population appears in the form of pulse.When we study epidemic models,and consider economic factors,pulse vaccination strategy is usually adopted.So the SIRS epidemic model is established in this paper and is a better explanation for this kind of infectious diseases.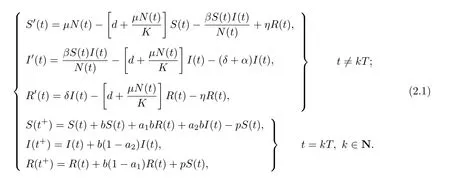
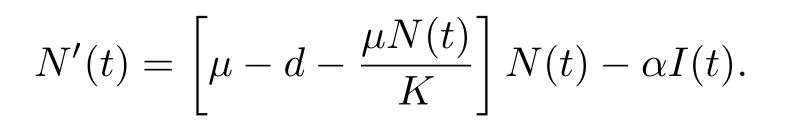
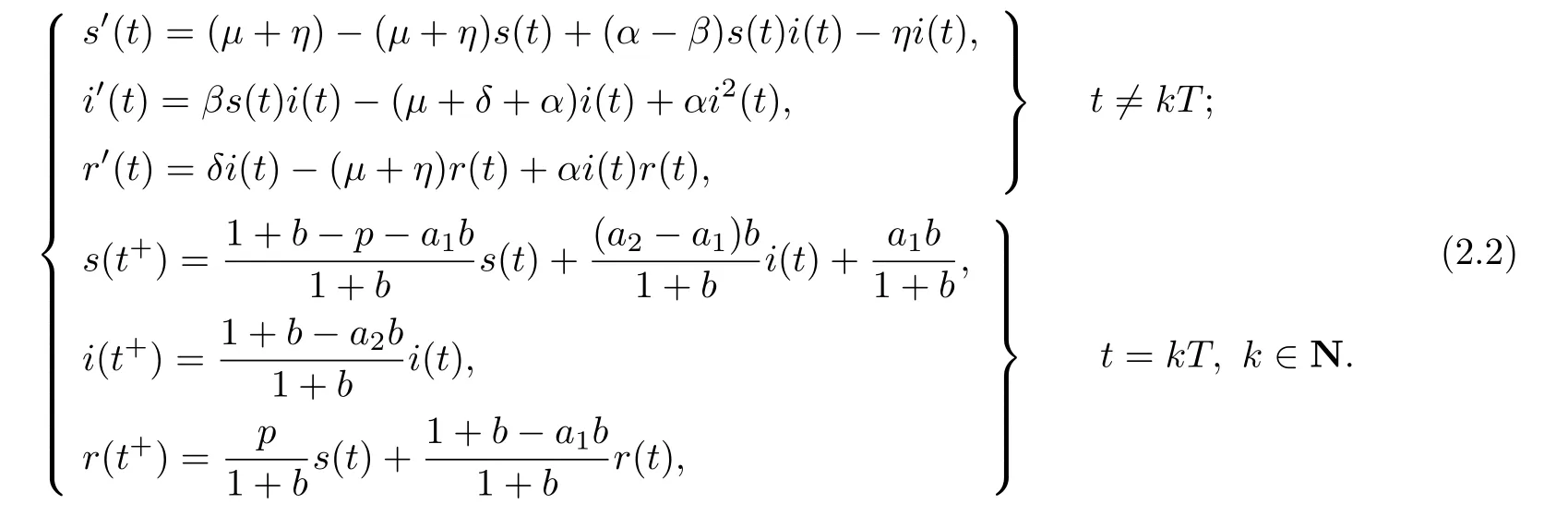
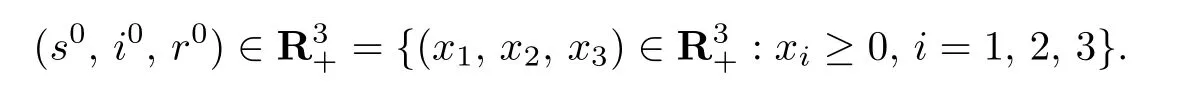
3 Global Stability of the DFPS
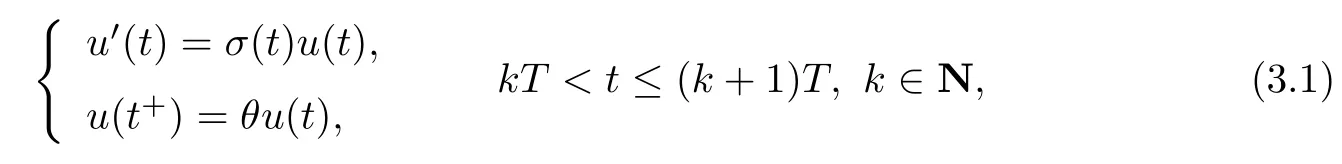
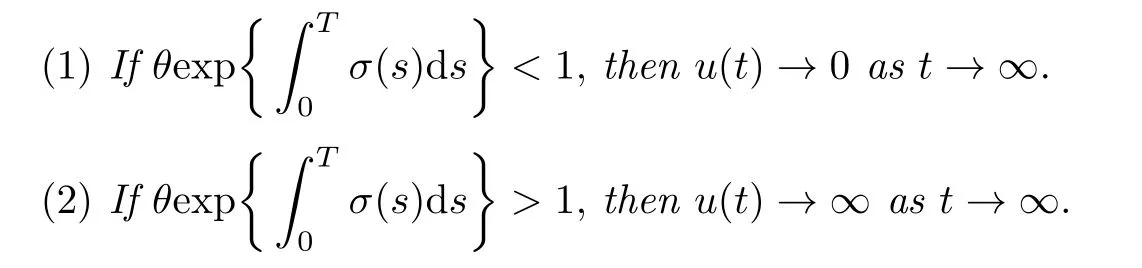
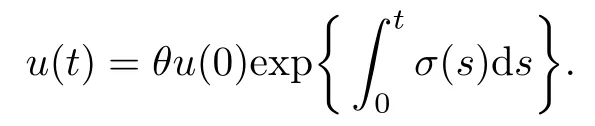

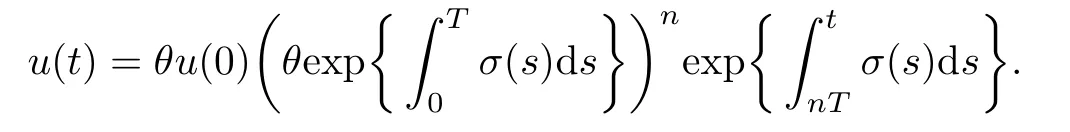



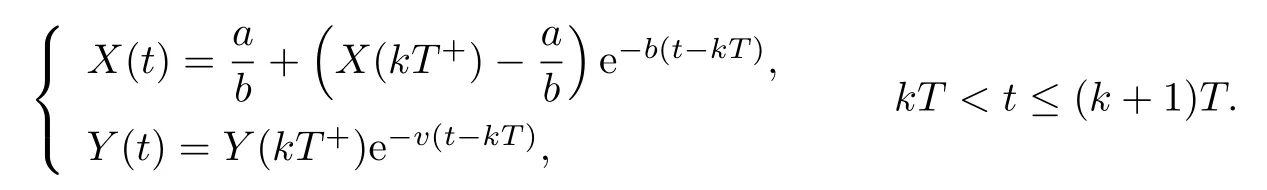
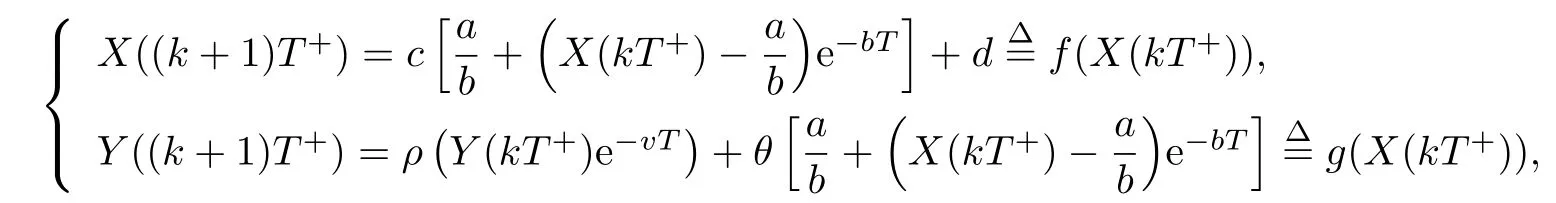
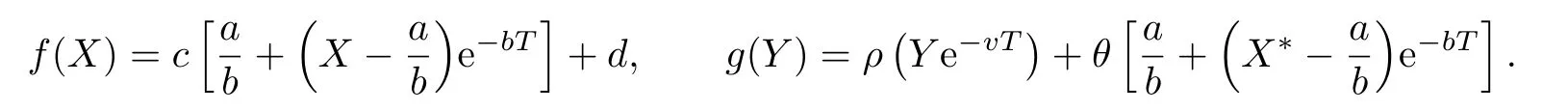
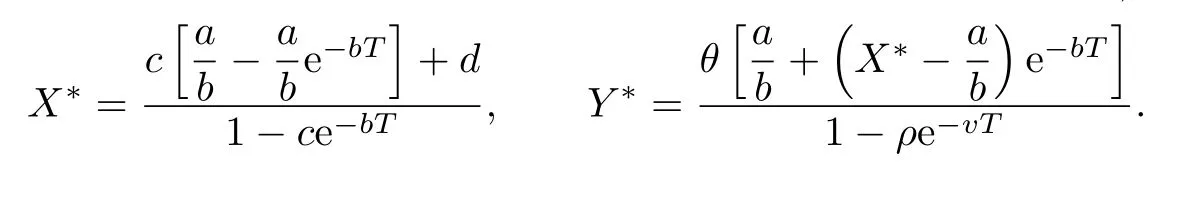
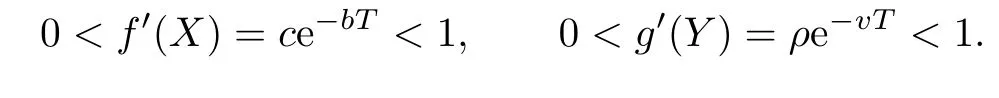
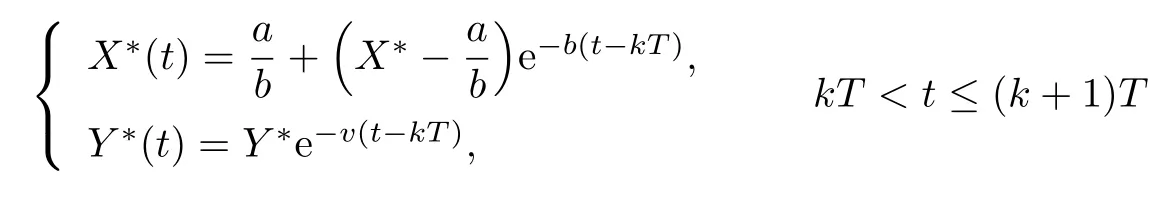
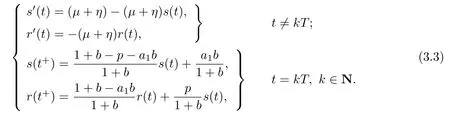
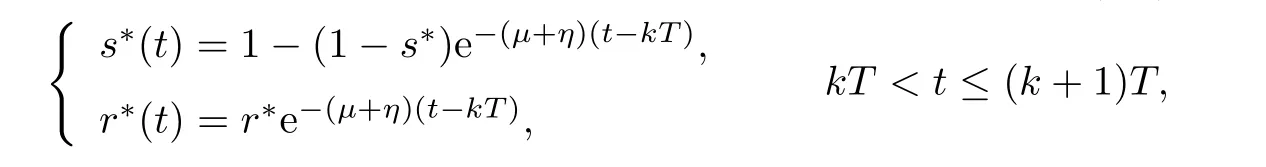
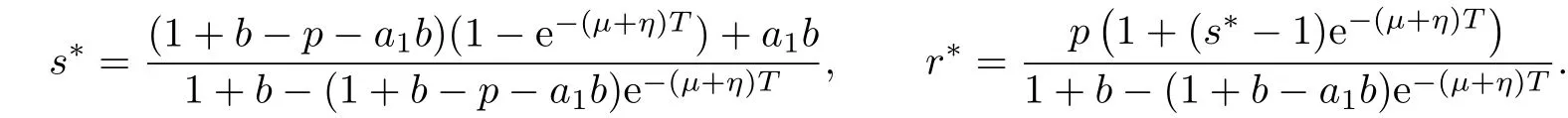
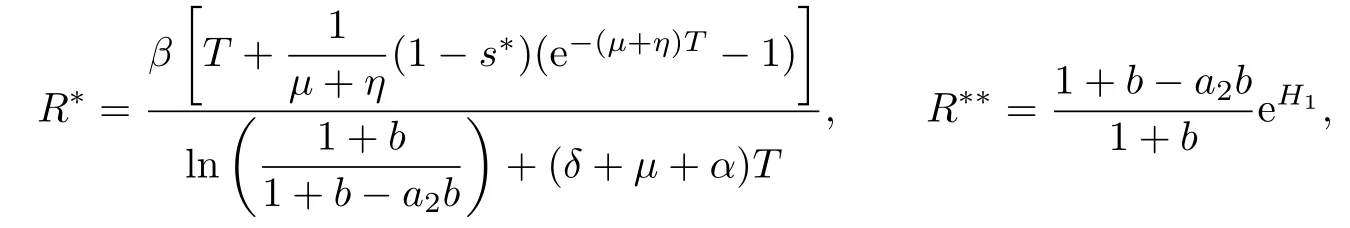
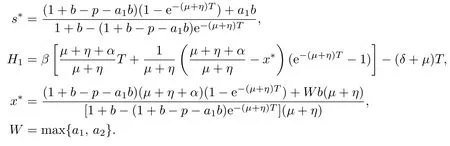
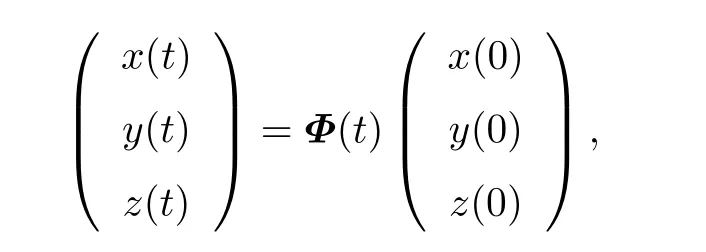
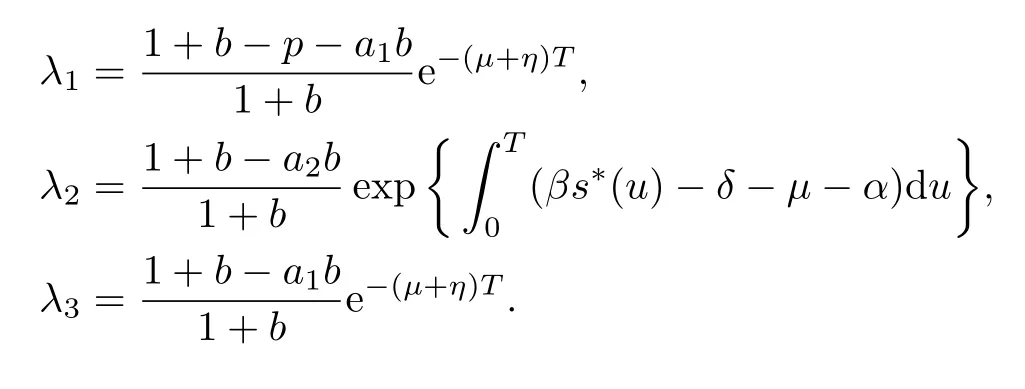
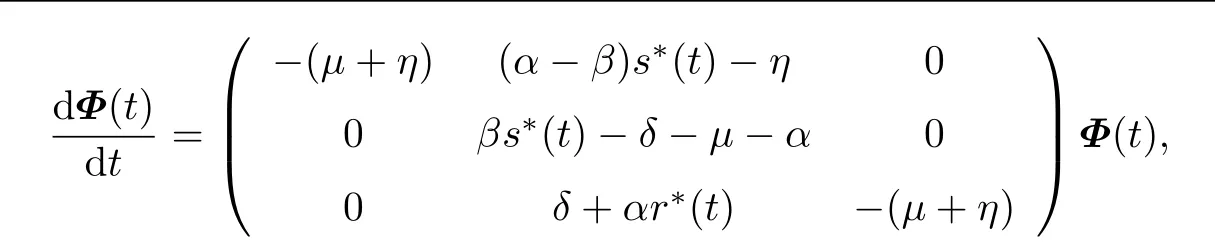

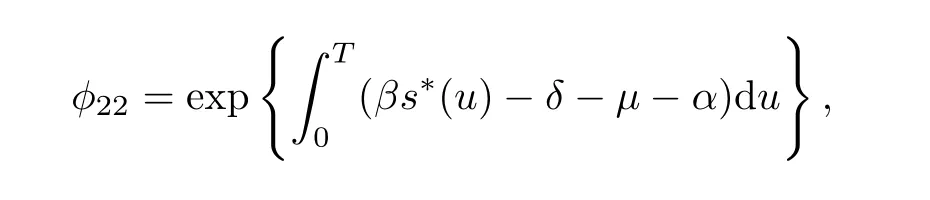
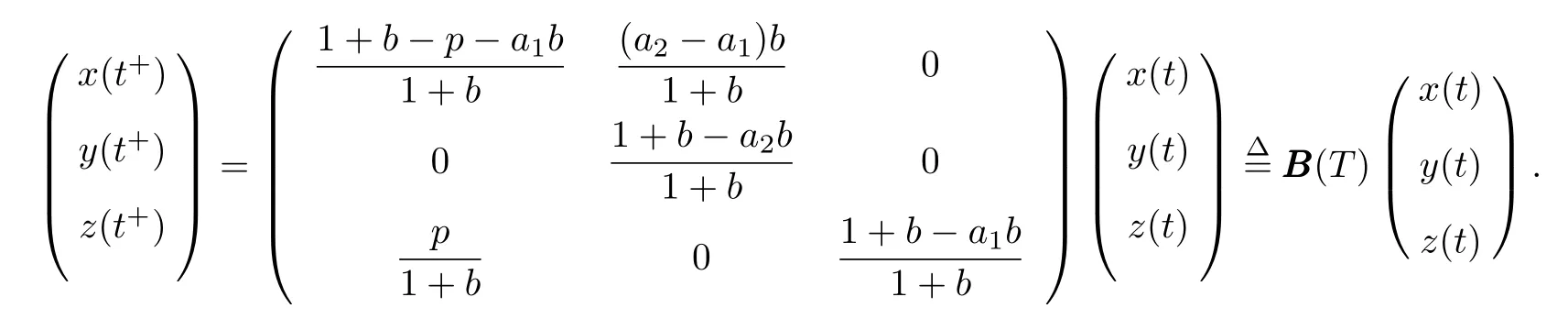




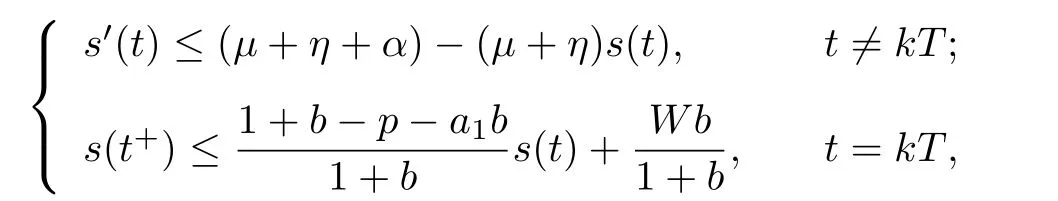
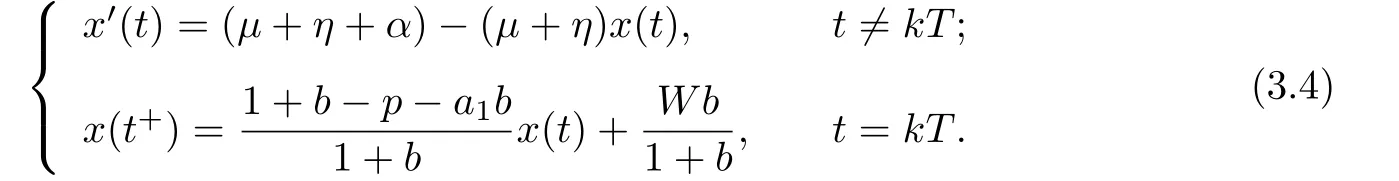

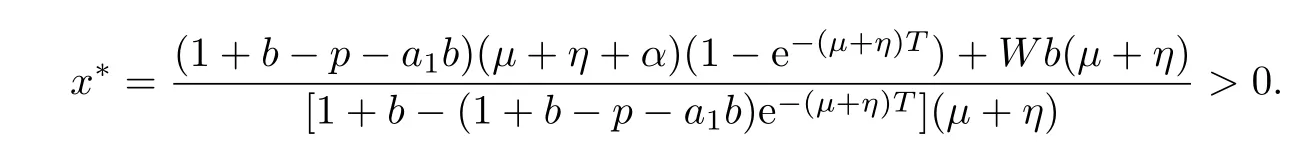

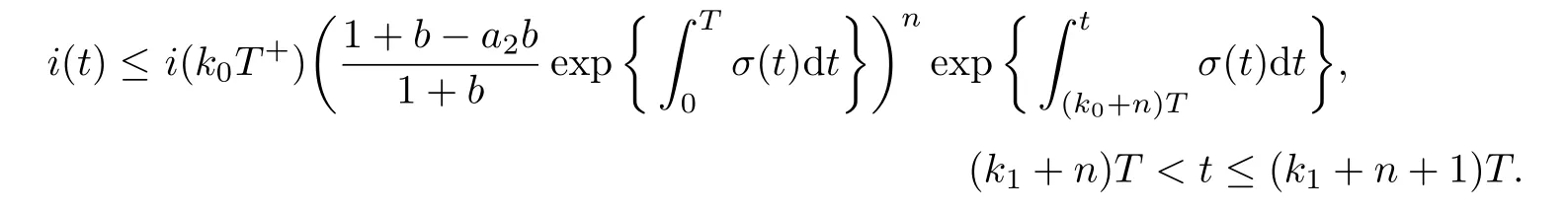

4 Permanence of Model
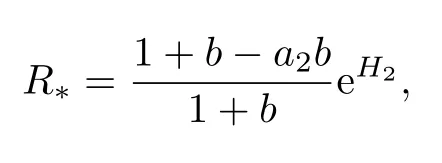
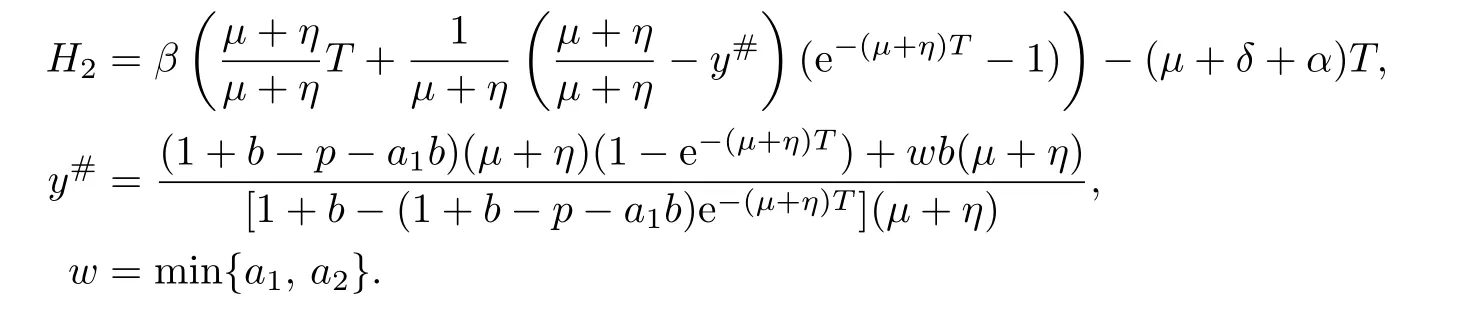
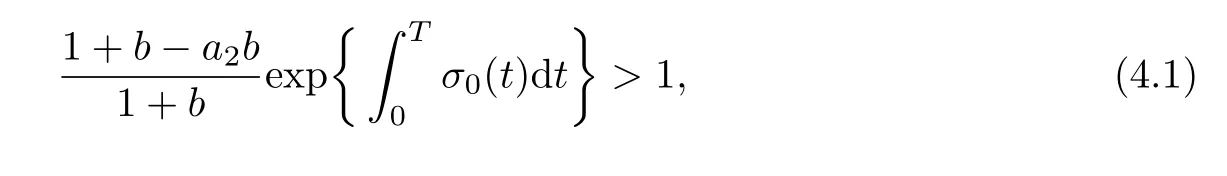
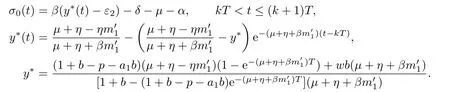

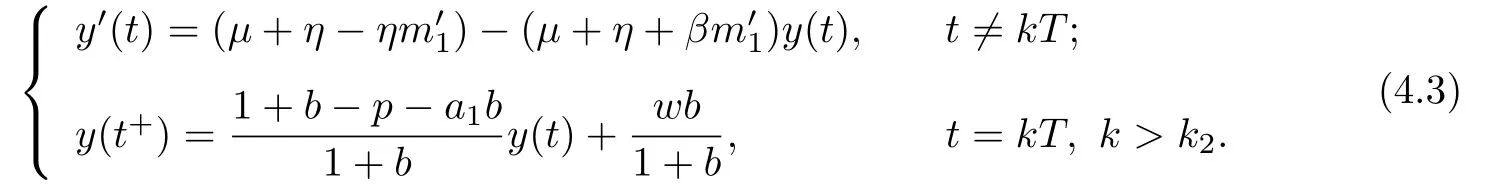
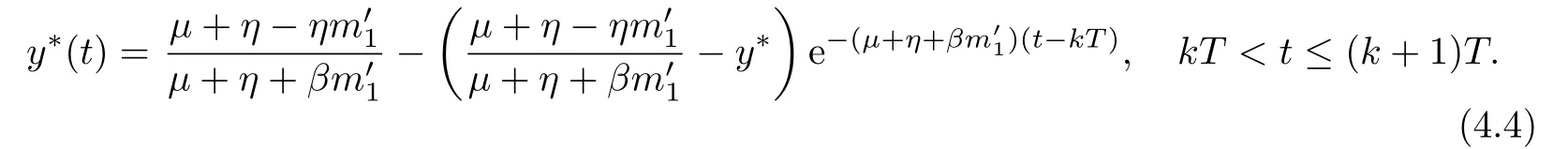
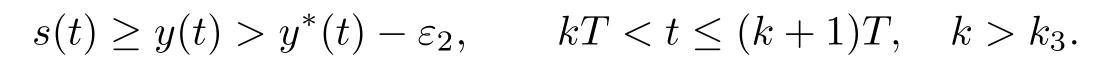
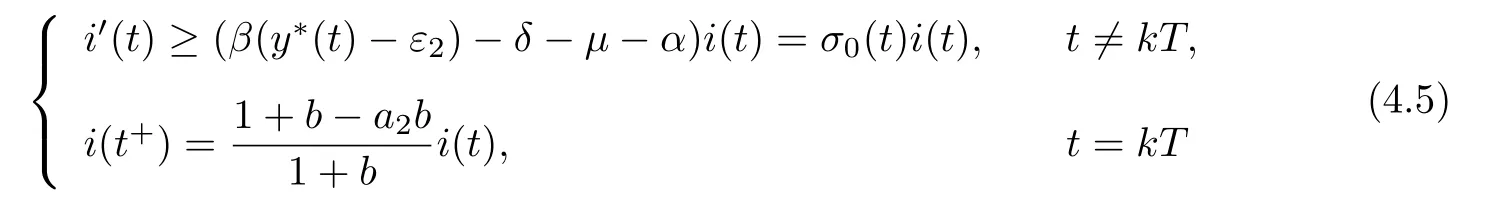
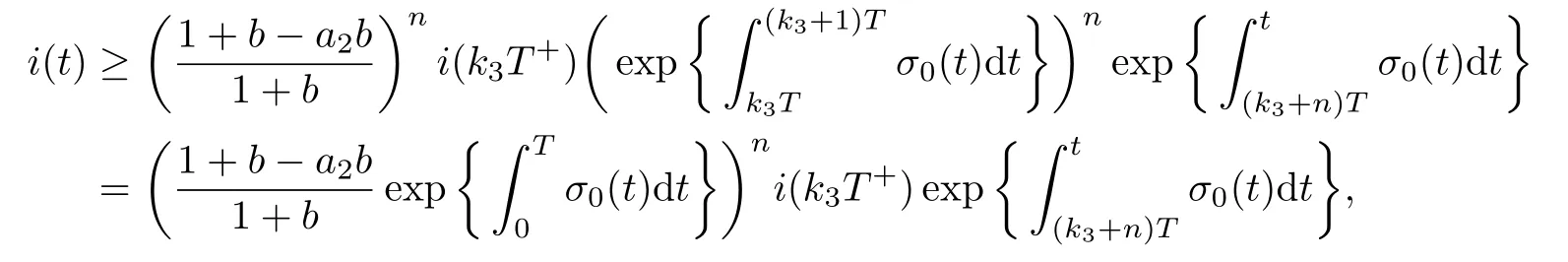

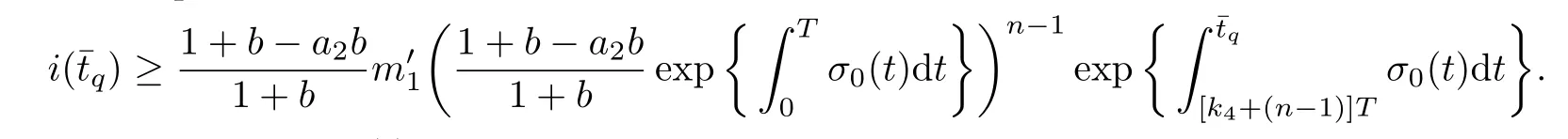
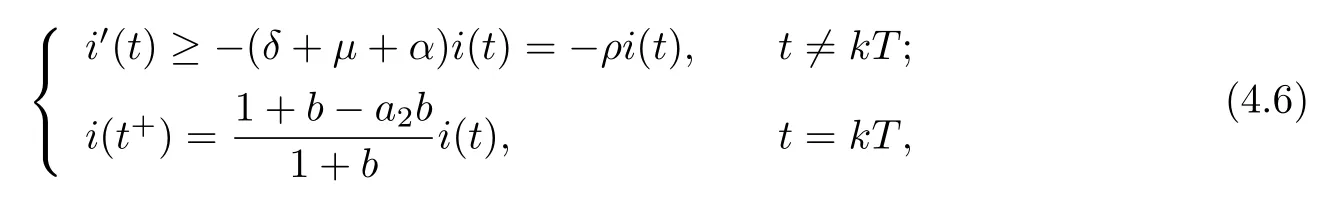
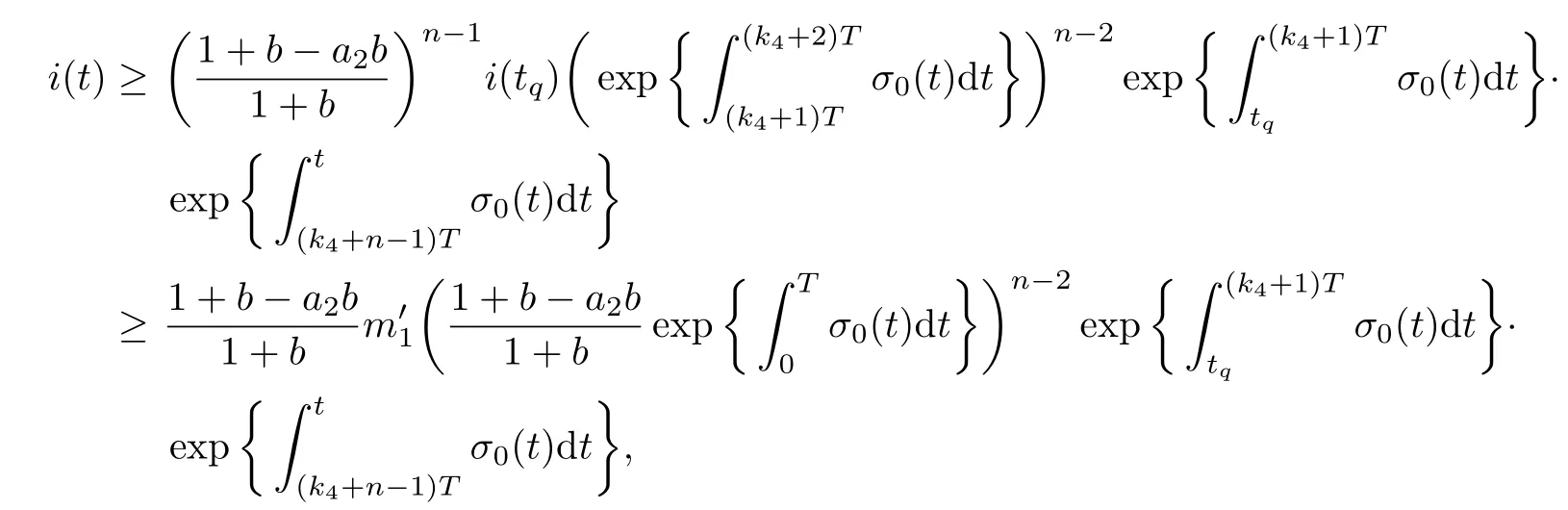
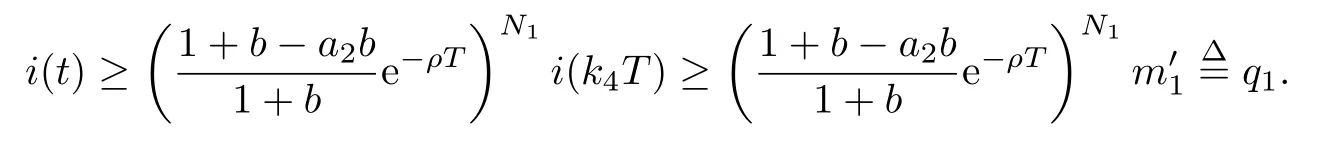
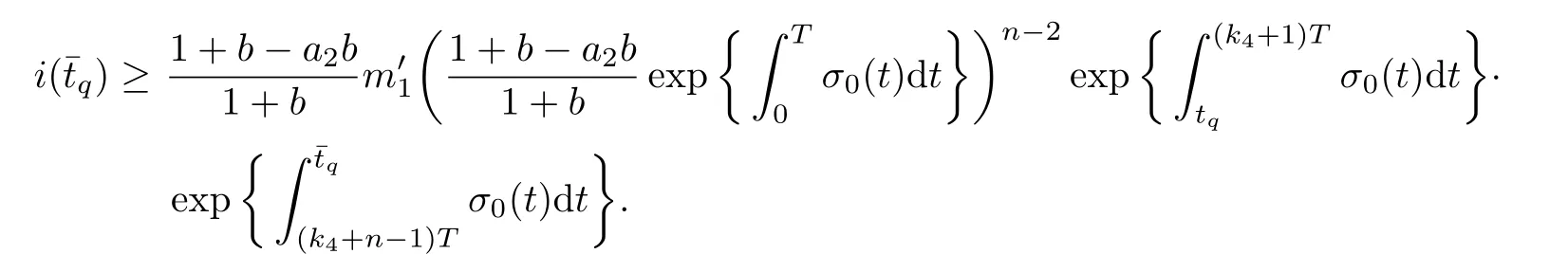
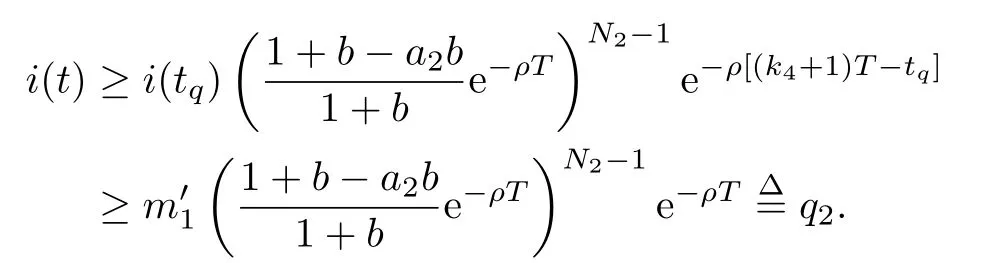
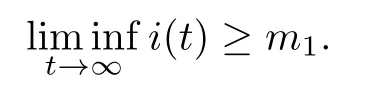
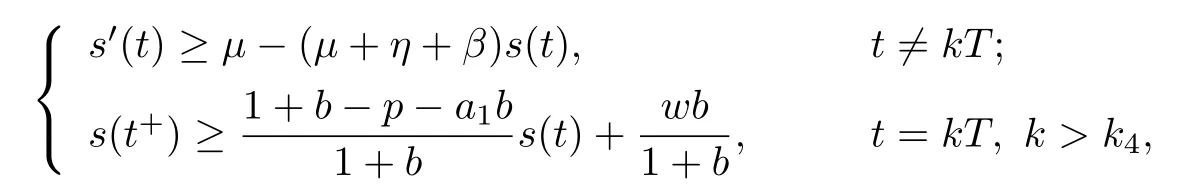
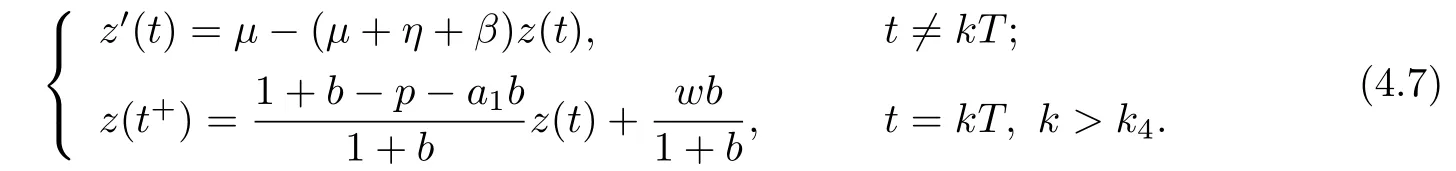
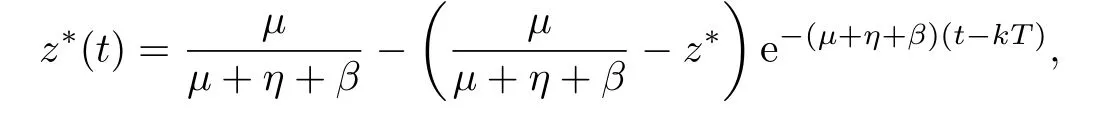
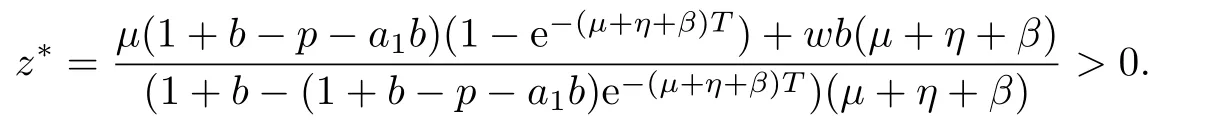
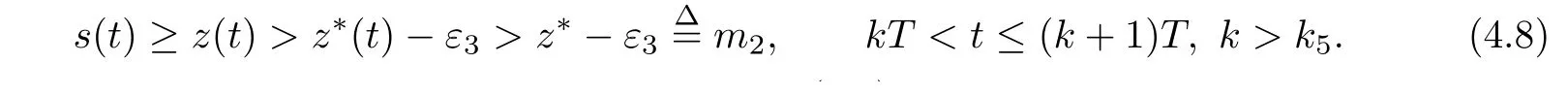
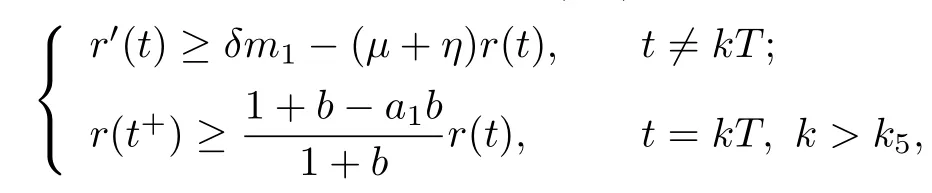
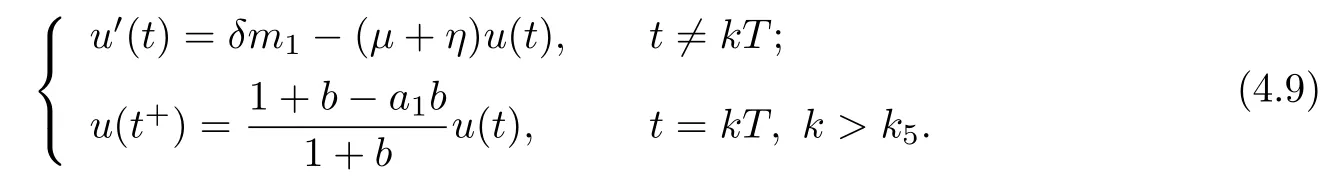

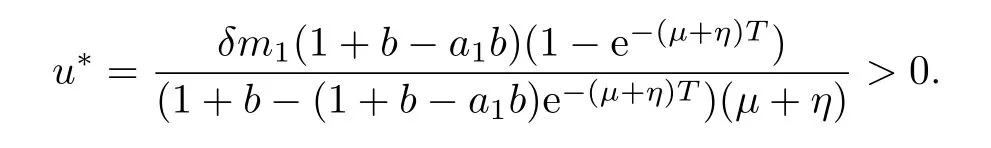
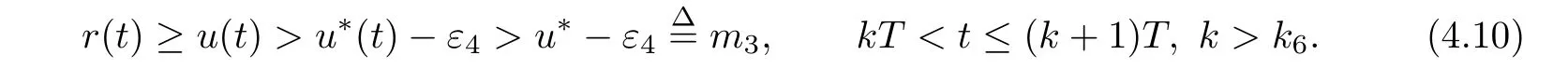
5 Numerical Simulation





6 Summary
 Communications in Mathematical Research2019年3期
Communications in Mathematical Research2019年3期
