直线式公交车停靠站对交通流随机延误的影响

周志俊

(贵州省交通规划勘察设计研究院股份有限公司，贵州贵阳 550081)

0 引言

直线式公交车停靠站具有建设简单、成本低等特点，被许多城市普遍采用。公交车运行停靠服务期间需占用一定的道路空间资源，对后续交通流产生不确定性影响。陈琳莉等[1]研究公交车停靠不同站台时对相邻车道车辆速度的影响。韦佼等[2]根据交通波理论，运用VISSIM仿真验证直线式公交车停靠对经过的社会车辆产生的影响。姚志洪等[3]研究公交车停靠随机延误对交通流的影响，并建立异质交通流车队流量离散模型。刘云等[4]建立直线式和港湾式公交站点的延误模型。Fitzpatrick等[5]分析公交车停靠的全程延误影响。直线式公交车停靠理论的相关研究对于公交都市建设具有重要意义，也可为道路上下游交叉口信号控制提供理论参考。

本文根据后续交通流的到达模式，分别建立折线式交通流随机延误模型和直线式交通流随机延误模型，分析直线式公交车停靠站对交通流随机延误的影响，并通过实例对模型进行验证，以期减少公交车停靠对后续交通流的影响，更好的促进城市交通的发展[6-20]。

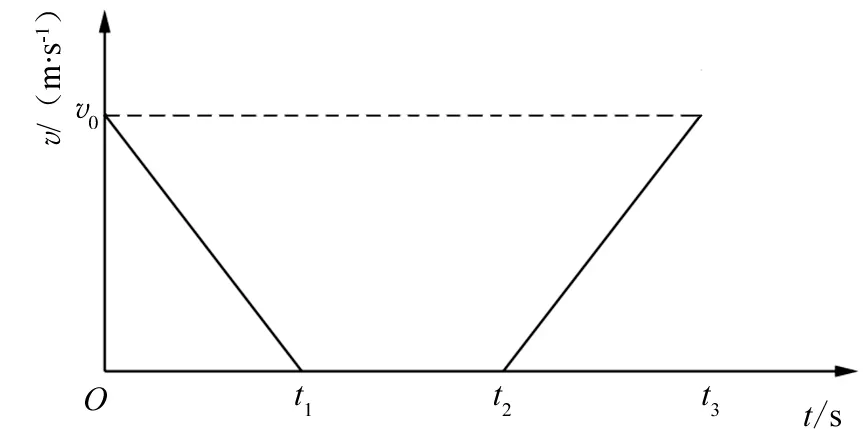
图1 公交车停靠运行速度变化

1 公交车停靠运行状态分析

根据相关研究，公交车停靠运行状态可分为减速进站、停靠服务、加速出站3个过程。图1为公交车停靠运行速度变化过程。其中t1为公交车减速进站时间，t2为公交车减速进站时间与停靠服务时间，t3为公交车减速进站时间、停靠服务时间及加速出站时间，v为公交车的行驶速度，v0为减速进站的初始速度(假设与加速出站的末速度相同)。

公交车减速进站时间

t1=v0/a，

(1)

式中:a为进出站时的加速度，加速度取固定值。

公交车停靠服务时间

Δt1=t2-t1=Qkt0/nd+t′，

(2)

式中：Q为公交车容量；k为在停靠站上下车乘客总数与车容量之比，一般k=0.1～0.4；t0为每个乘客上车或下车所用的时间，s，平均约2 s；nd为车门数；t′为常数，t′=3.5 s。

公交车加速出站时间

Δt2=t3-t2=v0/a。

2 公交车停靠运行期间后续交通流到达模式分析

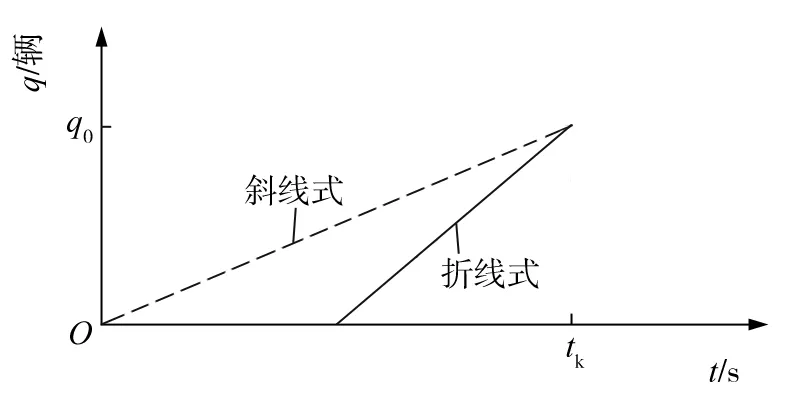
图2 两种交通流达到模式

公交车停靠直线式站台运行期间，根据后续交通流到达率λ和疏散率μ之间的关系，后续交通流存在两种到达模式，即折线式与斜线式。折线式到达模式视为交通流离散到达的一种状态，λ<μ，这种状态一般不易形成交通拥堵。斜线式到达模式视为交通流连续到达的一种状态，λ>μ，由于车流连续跟进，公交车在停靠运行时，容易形成交通瓶颈，造成交通阻塞。

两种交通流的到达模式分别如图2所示，图中q为交通流量，q0为某一固定的交通流量,tk为公交车停靠运行的时间。

3 折线式交通流随机延误模型建立

假设在某段时间内，折线式公交车停靠站台处到达的交通量较小，且行驶的机动车没有受到上游交通信号灯的干扰，用泊松分布计算这段时间内到达的车辆数。

根据折线式交通流的到达状态，公交车在折线式站台停靠运行服务期间，后续交通流的到达服从泊松分布，因此，单辆公交车停靠、占用车道延误交通流的总延误

(3)

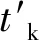
假设在某个折线式公交停靠站处，公交车辆的到达频率为β辆/h，由式(3)得单位时间内多辆公交车造成的后续交通流总延误

(4)

4 斜线式交通流随机延误模型建立

4.1 假设条件

1)斜线式公交车停靠站处前后100 m内没有信号灯控制的交叉路口。

2)公交车在未减速之前与后续跟进车辆保持相同的行驶速度v0，连续交通流在受到公交车停靠运行影响之后，运行速度降低，但仍以最大安全行驶速度v1行驶，直至达到正常行驶速度v0。

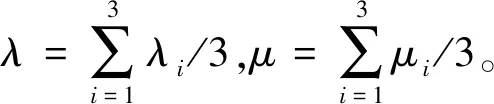
4)公交车在减速进站和加速出站过程中，到达率、疏散率及时间存在以下关系：λ1=λ3，μ1=μ3，t1=Δt2。

4.2 公交车减速进站和加速出站的排队车辆数

公交车在进站前进行减速行驶，这期间车辆的到达率大于疏散率，车辆形成排队现象，如图3所示。公交车减速进站期间，非公交车辆的λ1和μ1之间的关系如图4所示，图中kj为交通阻塞密度。

图3 公交车减速进站 图4 后续交通流到达率与疏散率之间的关系

则排队等候减速进站的车辆数

q1=(λ1-μ1)t1，

(5)

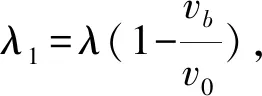
因此式(5)变为

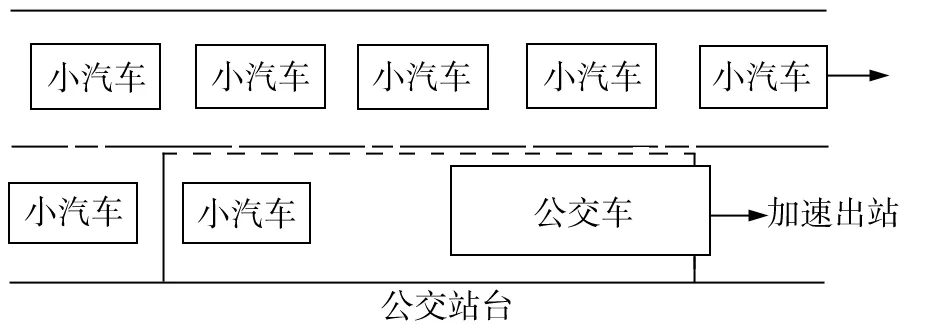
图5 公交车加速出站

公交车离开停靠站台进行加速行驶，速度由0加速到正常行驶速度v0。公交车加速运行状态如图5所示。

参考公交车减速进站推导公式，可以得出加速过程中排队等候的车辆数

(6)

由式(6)得公交车在直线式站台减速行驶和加速行驶期间的后续交通流排队等候的车辆数

(7)

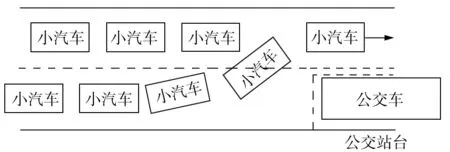
图6 公交停靠服务过程

4.3 公交车停靠服务期间的排队车辆数

在公交车停靠运行服务期间，后续交通流会形成排队和换道插车现象，如图6所示。

停靠服务过程中排队等候车辆数

q2=(λ2-μ2)Δt1。

(8)

4.4 公交停靠交通流随机延误模型

由式(7)(8)得公交车停靠运行造成的排队车辆数

(9)

公交车在加速过程中，速度达到正常行驶速度时，公交车对被干扰车辆不再造成影响，此时被干扰车辆的疏散率为μ0，μ0>λ>μ。所以此时排队车辆疏散所用时间,即交通流延误可以根据车流波动理论计算：

(10)

由式(9)(10)得

(11)

则由式(1)(2)(11)计算得单辆公交车的总延误

假设某路段有m个直线式公交站点，在单位时间内有n辆公交车在该路段停靠运行服务。可知，在单位时间内，运行在该路段上的n辆公交车在m个直线式站台处对后续交通流造成的总延误

i=1,2,…，m;j=1,2,…，n。

(12)

5 实例验证

选取某市某双向六车道路段，具有中央分隔带，没有机动车与非机动车隔离带，有一个直线式公交站台。通过该路段并进行停靠运行服务的公交线路有3条，且运行服务的公交车型相同。由调查情况可知，该路段存在早晚交通流不同的情况。根据流量的变化将调查时段分为2段，后续交通流到达模式分别为斜线式与折线式，即 7：50—8：50时段后续交通流到达模式为斜线式，15：50—16：50时段后续交通流到达模式为折线式。

根据调查及检测数据并计算得：t1=Δt2=11.7 s,vb=3 m/s，Δt1=23.5 s，v0=12 m/s，λ=0.36辆/s，μ=0.27辆/s。

1)7：50—8：50时段

该时段λ>μ，服务公交车有13辆。根据调查及检测数据并计算得，λ2=0.5辆/s，μ2=0.20辆/s，μ0=0.7辆/s，v1=4 m/s。将相关数据带入式(12)，得到运行在该路段上的公交车在斜线式站台处对后续交通流造成的总延误D′=1 252.55 s，则每辆车的平均延误为1 252.55/13=96.35 s。

2)15：50—16：50时段

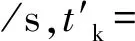
表1 数据处理结果

43.4 s，v′=10 m/s，将相关数据带入式(4)，得到运行在该路段上的公交车在折线式站台处对后续交通流造成的总延误D=18.835 s，每辆车的平均延误为18.835/12=1.57 s。

相关统计数据和计算结果统计如表1所示。

6 结论与建议

1)公交车在直线式公交站台停靠运行服务期间，会对后续交通流造成一定影响。当后续交通流的到达率小于疏散率时，公交车停靠运行服务造成的干扰较小，后续交通流能顺利通过；当后续交通流的到达率大于疏散率时，公交车停靠运行服务对后续交通流干扰较大，导致该路段容易形成交通瓶颈，交通流溢出，阻碍后续交通流正常运行。

2)公交车进站停靠运行会导致后续交通流滞后，通过对同一路段不同时间段的调查结果分析发现，这种滞后性在到达率大于疏散率时表现得比较明显。

3)公交车停靠运行对交通流的影响具有时空分布不均性，同一路段不同时间段，公交车停靠对交通流延误时间不同。

4)建议将直线式公交站台改建为港湾式公交站台，以减少公交车停靠对后续交通流的影响；没有条件改建的直线式公交站台，在确定站点位置时，需要与上下游交叉口保留足够的距离；直线式公交站台在上下游交叉口的交通控制上，应给予公交车优先通行权。