中国近海台风强度与水产品产量相关性分析

边 旭，吴云帆，郑 艳，宁鹏飞

（国家海洋信息中心，天津 300171）

引 言

台风对海洋生态系统扰动剧烈，近年来，台风对海洋生物和非生物环境的生态效益成为国内外研究的热点之一。随着全球气候变暖，台风发生频率增加，研究其对海洋渔业的影响愈发重要。很多学者也从多方面对影响台风的要素进行了研究，取得了一些成果。赵昕等（2013）基于IPCC报告中对脆弱性的定义，从敏感性和环境适应性两个方面建立了沿海地区经济系统海洋灾害脆弱性评价模型[1]。并以山东省台风灾害为例，讨论了2001-2011年间敏感性和适应性的变化规律。陈香（2007）通过分析，建立了台风灾害发生过程和灾害发生以后的脆弱性评估指标体系和评估模型，构建了台风灾害系统脆弱性综合指数模型，并以福建县域为单元，对福建省台风灾害系统脆弱性过程进行评价[2]。许多学者也做了类似的研究工作，并取得了很多成果[3-4]。高文（1991） 根据福建省水产厅统计结果，讨论了该省在连续遭受7次强台风袭击和影响的重灾之下，海洋捕捞总产量仍超额完成了“七五”计划指标，实现连续12年持续增长，年递增率达10%。并将之归结为渔船技术改造取得的成效[5]。刘超等（2010）针对宁波、舟山的渔业，应用风险分析模型，从灾损度、脆弱度及防灾系数3方面定性分析了台风灾害对渔业的影响[6]。叶海军等（2014） 利用Aqua卫星搭载的MODIS传感器数据，分析了慢速移动的强台风“鲶鱼”对中国南海北部海表面温度（SST）、海表面叶绿素a浓度、初级生产力和渔业资源的影响[7]。结果显示慢速移动的强台风对于渔业资源生产量有较大影响。Small等（2008） 在四个海区（黑潮区、湾流区、南大西洋和Agulhas Return Current附近） 对比了空间高通滤波QuikSCAT风应力大小和海水表面纬度（SST），发现二者呈现惊人的同位相变化，二者的空间相关系数均在0.38以上[8]。同时在其他海区也发现了类似的海表面风速与SST同相位变化的现象[9-12]。本文从数据变化趋势入手，针对台风对海洋自然生产水产品产量的影响，结合希尔伯特—黄变换分别对长期趋势变化的相关性和短期变化的相关性进行了讨论和分析，从而获得此两类数据的相关特性，从一个新角度建立起台风与海洋渔业经济的关系。

1 数据提取及模型化

海洋中水产品产量是海洋经济的重要组成部分，水产品产量包含全社会人工养殖的水产品和天然生长的水产品捕捞量两个部分。本文重点针对台风强度变化对自然条件下的水产品产量影响进行讨论分析。而根据前期讨论[13]，台风的强度变化可由台风中心附近的最大风速反映，故选取我国周边区域的台风风速与海洋产品产量两类数据，分析其相互关系。以下分别对这两类数据模型的提取和建立进行讨论。

1.1 天然生产海水产品产量数据模型

针对天然生产海水产品产量Q（t）进行分析，其中1954-1985年数据来源于《中国渔业统计年鉴 （2005）》[14]，1986-2017年数据来源于 《中国渔业统计年鉴 （2018）》[15]。令其按照时间变化曲线如图1所示。

根据定义，R（t）表示每年天然生产海水产品产量与上一年天然生产海水产品产量的比率。

1.2 台风风速数据模型

图1 历年天然生产海水产品产量与上一年产量比率

针对中国周边西北太平洋海域，一些学者对不同数据来源的台风数据进行了分析和对比[16-17]，分析结果表明此区域内CMA数据集[18]较为准确且全面，故参考CMA所发布的台风数据，选取1949-2016年所有观测风速数据绘制空间风速强度图。为了更好地说明风速强度空间分布情况，应用kmeans聚类[19]方式对数据按照空间-最大风速（MSW）进行聚类分析，聚类结果如下图所示:

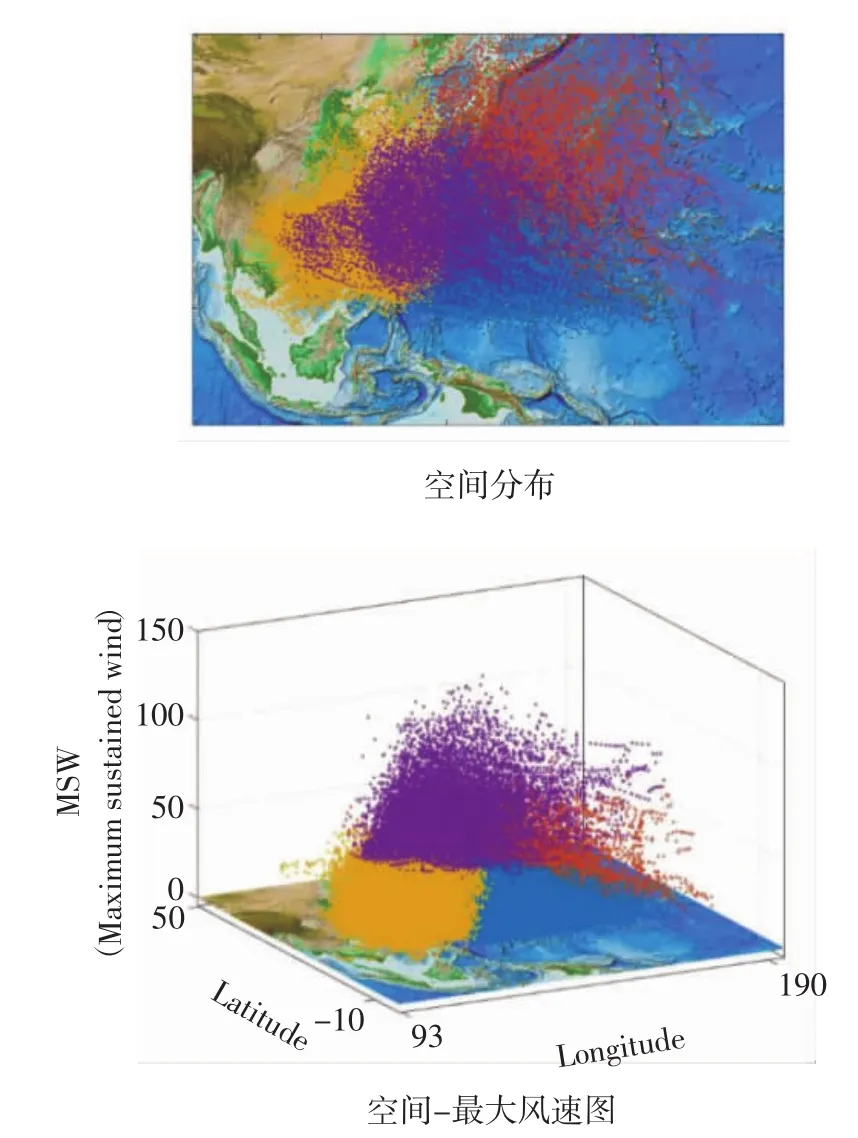
图2 台风数据聚类图

如图所示，选择聚类结果中样本丰富区域120°-140°E，15°-30°N 进行分析讨论，按照年—月—风速三个纬度绘制图像如图3所示。

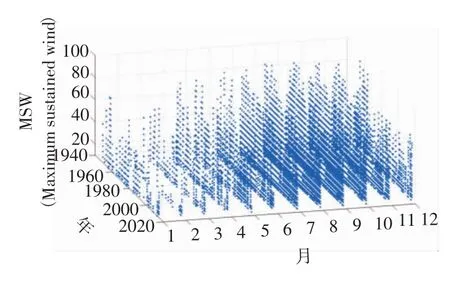
图3 台风年-月-风速三维图

从图3中可以得出，在该地区每年数据分布较为平均，台风在7-10月出现较多且最大风速值较大。进一步针对该图中风速—年维度投影进行分析，并将MSW的最大值用曲线连接，即其上包络线FMSW（t）如图4所示。

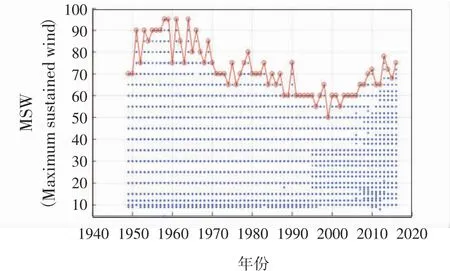
图4 年-风速关系图

为了进一步表征该区域下历年风速变化剧烈程度，令Dtyp（t）=Vmax（t）-Vmin（t），其中Vmax（t）与Vmin（t）分别表示t年该区域中风速最大和最小值，而根据实际情况Vmax（t）=RMSW（t），Vmin（t）=0，则Dtyp（t）=RMSW（t），即可认为该区域中台风FMSW（t）可表征风速最大偏差值随时间的变化情况Dtyp（t）。

2 数据分析及讨论

对Dtyp（t）和R（t）进行相关性分析，令

其中 τ=0，1，…，N-1，t∈ （1954，2016），N=63，即求得Dtyp（t）与R（t）的互相关度。相关性曲线如下图所示:

图5Dtyp（t）与Q（t）的互相关度曲线

对Dtyp（t）与R（t）做显著性检验，检验结果表明二者无显著性关系，即可认为Dtyp（t）和R（t）之间不存在相关关系，相关度曲线所表征的相关度强度值不能表征数据普遍相关性。

参考图5相关性结果可得，Dtyp（t）与R（t）的最大相关系数为0.356 2，但并不显著。根据显著性检验的数学定义[20]，可以认为其相关度最大值来自数据的抽样误差。根据图1和图4分析得到，原始信息可以认为为非平稳信号序列，其中存在明显的长期变化的趋势，且相对短期变化部分能量较大（约一个数量级），导致数据抽样误差较大，另一方面结合式（1），令

其中D1（t）和R1（t）代表能量较大部分，D2（t）和R2（t）代表能量较小部分，则式（2）可变换为如下形式:

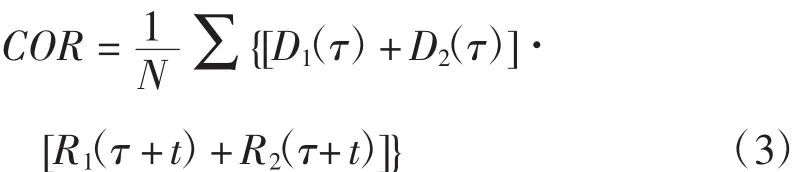
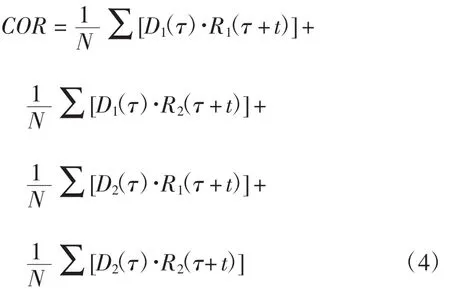
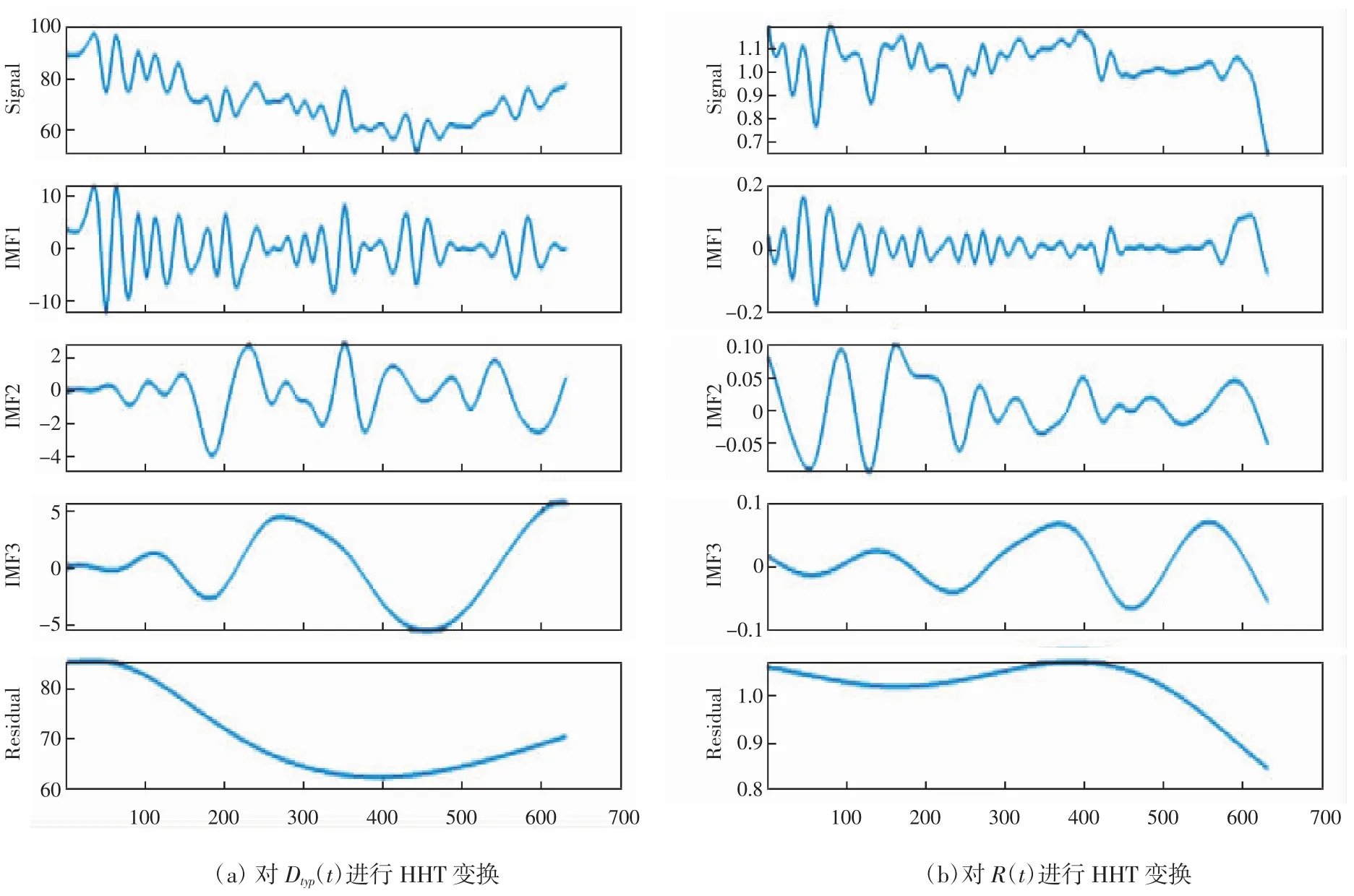
图6对Dtyp（t）和R（t）进行HHT处理后逐IMF数据

继续化简最终得到如式（4）所示:如式（4）所示，前三项在计算结果中所占比重较大，计算结果中无法直接获得能量相对较小部分（D2（t）和R2（t））相关性信息。为了去除能量较大的长时间尺度趋势信息对短时间尺度信息的干扰，更加全面地得到Dtyp（t）与R（t）相关性结果，针对不同时间尺度将Dtyp（t）与R（t）进行分解。本文采用希尔伯特-黄（HHT） 变换分别对Dtyp（t）和R（t）进行处理，该方法被认为是2000年来以傅立叶变换为基础的线性和稳态频谱分析的一个重大突破。其依据数据自身的时间尺度特征来进行信号分解，可以自适应地将任意复杂数据序列分解为一列本征模态函数（IMF）[21]，通过分析这些IMF可以分离Dtyp（t）与R（t）数据变化的不同时间尺度信息，更好地挖掘数据变化特点。应用HHT将Dtyp（t）与R（t）变换后分别记为Htyp（i）和HR（i），其中i=IMF1，IMF2，…，IMFn，…，IMFk，不同IMF即可理解为不同时间尺度下数据的变化趋势曲线。将变换后各IMF数据绘制如图6所示:

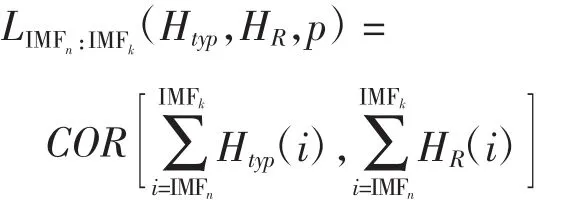
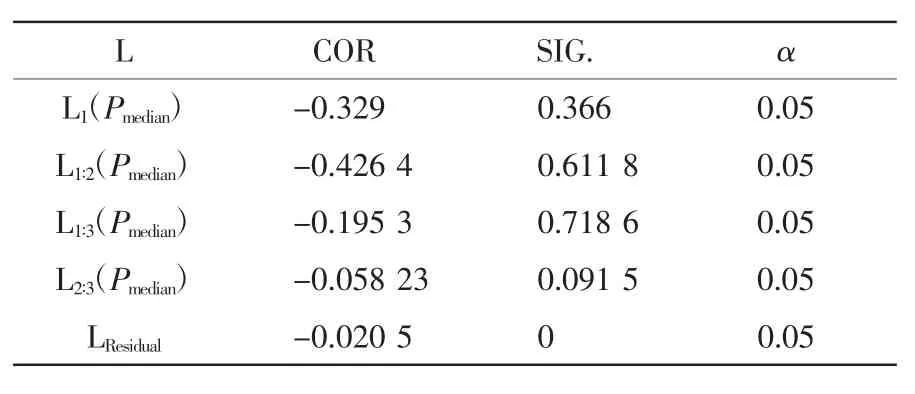
表1 互相关计算结果

如表1所示，显著性检验结果表明，除LResidual以外其余均不拒绝相关显著性假设（SIG.＞α），即均可认为具有显著相关性。分析相关系数变化规律可以看到，随着计算IMFn的增加，相关程度先增大后减小，其中L1∶2（Pmedian）相关系数绝对值最大，且达到一般相关水平。该结果表明，在去除长时间尺度趋势信息后，仅保留IMF1和IMF2数据时，台风风速强度差值Dtyp（t）和天然生产海水产品产量相邻年间比率R（t）之间显著存在一般负相关性。即可以认为台风风速最大值的增大会影响未来一年内天然生产海水产品年产量降低，反之亦然。另一方面根据L2∶3（Pmedian） 和LResidual结果表明，对于中长时间以及更长的时间尺度下，Dtyp（t）与之间并不存在明显相关性，即台风风速最大值的中长期变化趋势并不会对天然生产海水产品产量的中长期趋势产生显著影响。

3结论

（1）本文分析了我国周边区域的历年台风数据及我国的天然生产海水产品产量数据。根据表1结果发现在较短时间尺度下（2年以内），台风最大风速和天然生产海水产品产量之间显著存在一般负相关性，而对于更长的时间尺度（2年以上），并不存在此结论。即台风最大风速会对未来一年内的天然生产海水产品产量有显著的负向影响；而对于该产量的中长期变化趋势影响并不显著。

（2）本文针对两类来自自然科学以及经济学的时间序列数据进行分析。首先将两类数据分别抽象建模为非平稳信号序列，并利用希尔伯特-黄变换将抽象后信号按照不同时间尺度进行分离，分别将对应时间尺度的两类信号相关度进行分析，成功得到某一时间尺度的相关性信息。从一个角度建立起台风与海洋渔业经济的关系。也为此类信息挖掘提供了一个新的方法和思路。