舵和艉鳍对超大型集装箱船操纵性的影响

吴梓鑫, 陈伟民, 李建鹏

(上海船舶运输科学研究所 航运技术与安全国家重点实验室，上海 200135)

0 引 言

在船舶能效设计指数(Energy Efficiency Design Index,EEDI)和船舶能效营运指数(Energy Efficiency Operational Indicator,EEOI)等船舶能效法规强制执行，以及全球经济持续低迷和航运业竞争日趋激烈的背景下，集装箱船大型化的优势愈发明显。打造20 000 TEU以上超大型集装箱船创新链符合《中国制造2025》的战略要求，开展20 000 TEU以上超大型集装箱船专项科技工程可为“建设海洋强国”战略和“一带一路”倡议提供高端装备，具有重要的战略意义。

近年来，随着超大型集装箱船的市场化程度逐渐提高，超大型集装箱船的操纵性能研究越来越受关注。李俭[1]研究超大型集装箱船在受风情况下的操纵性能;李能荣[2]通过理论分析、模拟试验和实船操作,研究超大型集装箱船在反潮水离泊时采取的操纵措施;王化一[3]基于MMG方程建立四自由度船舶操纵运动数学模型，模拟研究大型集装箱船在拖船协助下满载航行时在港内的操纵运动。

舵和艉鳍的设计对船舶的操纵性有着至关重要的影响。陈伟民[4]通过模型试验研究不同舵型下船舶操纵性的变化;孙海素等[5]对公务船的线型和艉鳍等附体进行优化，使船舶的性能得以提高。然而,目前有关舵侧面几何形状对船舶操纵性的影响的研究较少。对此，本文以某超大型集装箱船为研究对象，采用自由自航模试验方式研究舵和艉鳍对超大型集装箱船操纵性的影响。

1 船舶操纵运动数学模型

图1 船舶运动坐标系

建立船舶运动固定坐标系O0-x0y0z0和以船舶重心G为原点的动坐标系G-xyz(见图1)。

对于船舶的操纵运动，若忽略垂向运动，可用船舶重心位置(x0G,y0G)和船舶中纵剖面与O0x0的交角ψ及其对时间的导数来表示。根据刚体质心运动的动量和动量矩定理，船舶运动的方程式可表示为

(1)

式(1)中：m为船舶的质量；Izz为船体绕通过重心的铅直轴的质量惯性矩；X0、Y0分别为船舶在O0x0方向和O0y0方向上的分力；N为作用于船舶上的外力绕z轴的回转力矩。

2运动坐标系在船舶运动中的转换关系为

(2)

记u和v分别为船舶瞬时速度在x轴和y轴上的分量，可得

(3)

将式(3)两边对时间求微分，并用r表示角速度，可得

(4)

对式(4)进行泰勒展开线性化处理，并略去二阶以上高阶小量，得到船舶操纵运动线性方程式为

(5)

(6)

式(6)又称为二阶线性KT方程。

(7)

由于船舶本身的惯性很大，操舵速度有限，一般转舵速度小于3 (°)/s，令

T=T1+T2-T3

(8)

得到船舶操纵运动一阶响应模型为

(9)

式(9)中:K为回转性指数，其本质是船舶定常旋回阶段船舶每单位舵角的角速度值,在一定的舵角下，K值越大，回转直径越小，船舶的回转性能越好;T为跟从性指数，反映的是操舵之后向船舶定常角速度趋近的快慢,T值越小，船舶进入定常回转的速度越快，船舶的稳定性越好。

为方便比较，一般将K和T转化为无因次形式,即

(10)

式(10)中:v0为回转初始速度。

2 试验参数

2.1 船舶模型尺度和螺旋桨尺度

船舶模型尺度见表1。螺旋桨采用侧斜桨，旋向为右旋,具体尺度见表2。

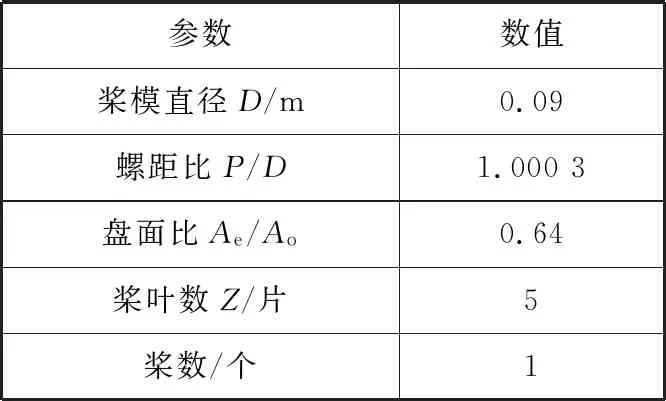
表2 螺旋桨尺度

2.2 舵参数

为研究舵面积和舵型对船舶的航向稳定性及应舵能力的影响，通过参考相关文献、向有关专家咨询和项目组讨论，设计4种舵方案进行试验研究，舵剖面均为NACA20翼型，各舵方案的参数见表3，各舵方案示意见图2。

表3 各舵方案的参数

a) 方案1

b) 方案2

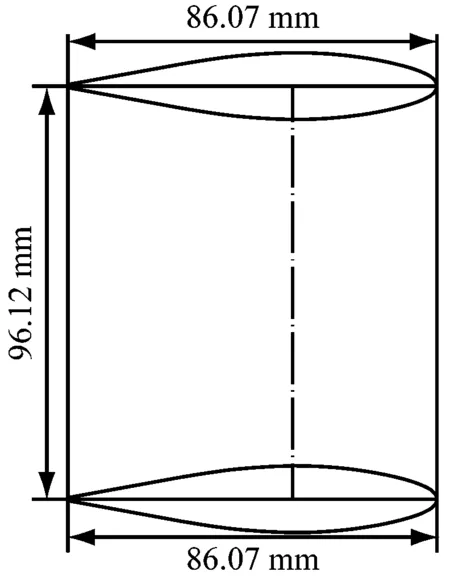
c) 方案3

d) 方案4

图2 各舵方案示意

2.3 艉鳍参数

为研究艉鳍面积对船舶的航向稳定性和应舵能力的影响，设计2种艉鳍方案,结合最佳舵方案进行试验研究。艉鳍参数见表4，艉鳍方案示意见图3。

表4 艉鳍参数

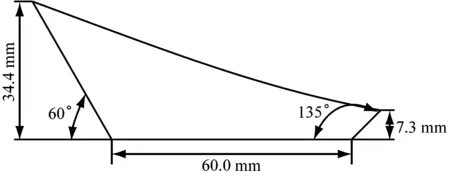
a) 艉鳍1 b) 艉鳍2

3 模型试验

在上海船舶运输科学研究所操纵水池进行模型试验，该水池长90 m，宽30 m，水深1 m，试验方式为船舶自由自航模试验，船模航速为0.97 m/s。试验内容见表5，包括Z形试验和回直试验。首先进行Z形试验，通过数据分析选取最佳舵方案;随后配合不同艉鳍方案进行回直试验。图4为船舶模型，图5为模型试验。

表5 试验内容

图4 船舶模型

图5 模型试验

4 结果分析

4.1 Z形试验

图6为Z形试验艏向角历时曲线，表6为4种舵方案Z形试验结果。

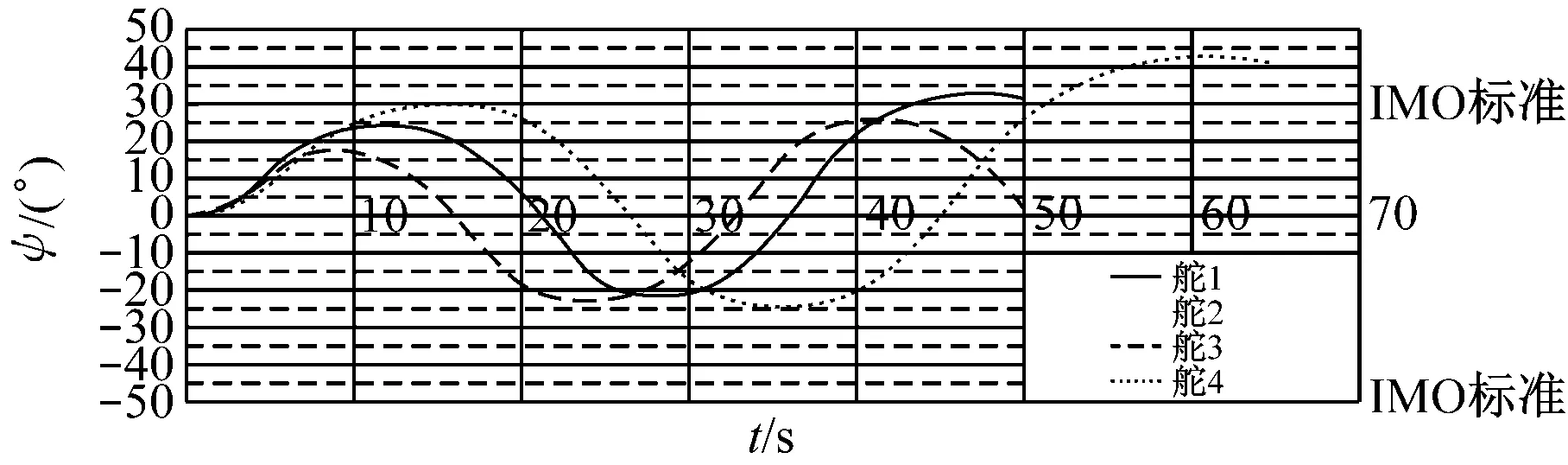
a) 10°/10°Z形试验

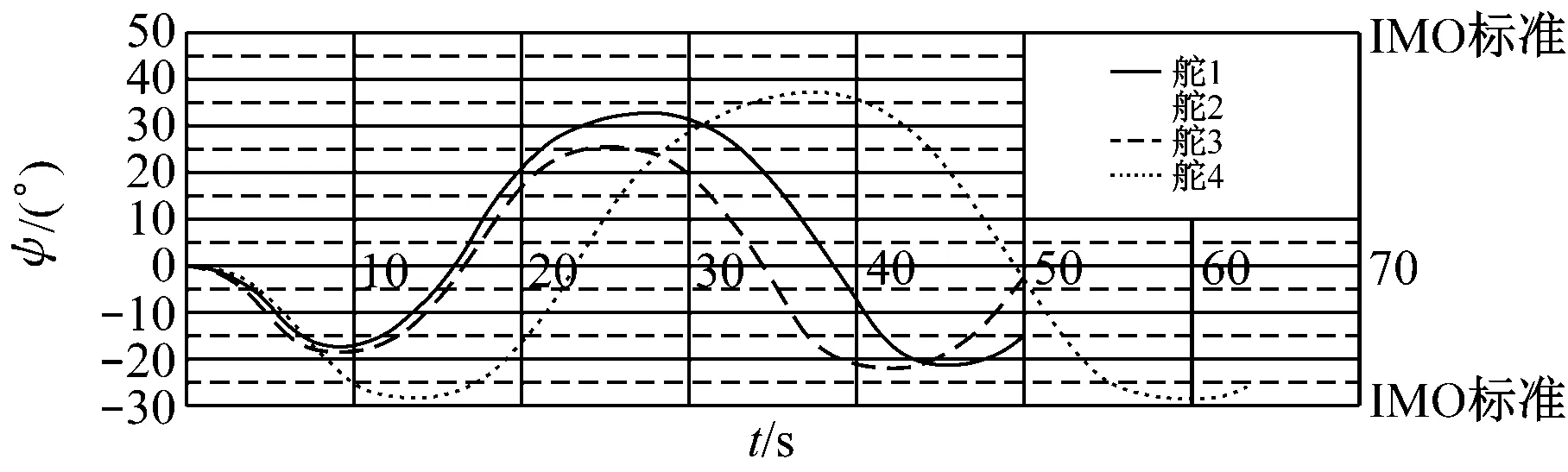
b) -10°/10°Z形试验

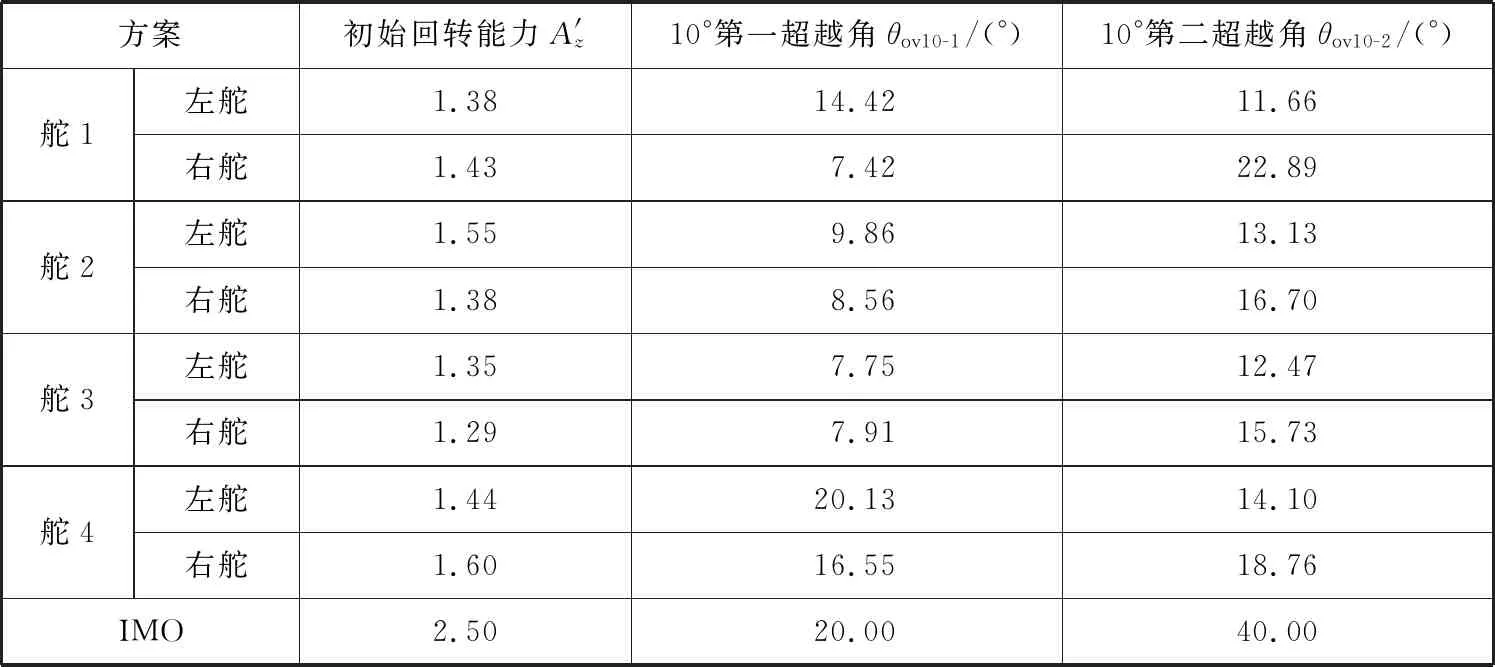
图6 Z形试验艏向角历时曲线

为方便分析，将舵3各结果数据记为1.00，则4种舵方案结果可转化为表7所示的数据。

表7 Z形试验数据处理结果

从表7中可看出，舵3的初始回转能力和超越角比其他舵方案都小，表明舵3为优选舵方案。因此,将舵3与2种艉鳍方案相结合进行后续试验,结果见图7和表8。

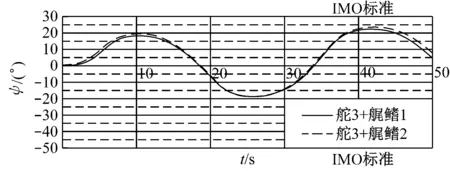
a) 10°/10°Z形试验

b) -10°/10°Z形试验

图7 Z形试验艏向角历时曲线(舵+艉鳍)

4.2 K指数和T指数分析

根据文献[6]中的K指数和T指数计算方法，列出各工况下回转性指数K和跟从性指数T的值(见表9)。舵1的面积与舵2相同，舵1的侧面为上端宽下端窄的梯形，舵2的侧面为矩形，舵1的回转性指数比舵2大4.6%，可见舵1的回转性能优于舵2;舵2的面积比舵3小8.5%，舵2的侧面和舵3的侧面均为矩形，舵2的回转性指数比舵3小10.1%，说明舵3的回转性能优于舵2;舵1的面积比舵4大11.1%，舵1的侧面和舵4的侧面均为梯形，舵1的回转性指数比舵4大9.3%，说明舵1的回转性能优于舵4。综合不同舵型和舵面积的回转性指数可知:对于目标船舶而言，梯形侧面舵型的回转性能优于矩形侧面舵型；当舵面积增加时，回转性能增强。

表9 K指数和T指数的值

增加艉鳍之后，工况4的回转性指数比工况3小8.7%，工况5的回转性指数比工况3小6.9%，结合艉鳍1的面积大于艉鳍2的面积，可认为船舶加装艉鳍相当于增加纵剖面积，降低其回转性能。

通过分析跟从性数据可知:舵1的跟从性指数与舵2相当，说明对于该类船舶而言，矩形侧面舵型和梯形侧面舵型对跟从性不敏感;舵2的跟从性指数比舵3大6.2%，说明舵3的跟从性优于舵2;舵1的跟从性指数比舵4小8.0%，说明舵1的跟从性能优于舵4。

增加艉鳍之后，工况4的跟从性指数比工况3小6.5%，工况5的回转性指数比工况3小3.6%，说明艉鳍的增加缩短了船舶应舵时间，增强了船舶的稳定性。

4.3 回直试验

表10为各方案下的回直试验剩余角速度数据。由表10可知:各方案下的剩余角速度均在0.12～0.23 m/s，说明该船本身具有较强的航向稳定性，舵面积和侧面形状对其航向稳定性的影响有限;增加艉鳍相当于增大船舶侧面积，其剩余角速度减小，说明增加艉鳍能在一定程度上增强船舶的航向稳定性。

表10 各方案下的回直试验剩余角速度数据

5 结 语

本文采用自由自航模试验方法，借助某超大型集装箱船模型，设计不同侧面舵型、舵面积和艉鳍方案，通过Z形试验获得回转性指数和跟从性指数,通过回直试验获得剩余角速度，分析舵和艉鳍对超大型集装箱船操纵性的影响。试验结果表明:在翼型和舵面积相同的条件下，梯形侧面舵型的回转性优于矩形侧面舵型；当舵侧面形状相同时，舵面积增大有助于增强船舶的回转性能；艉鳍的使用在操纵运动中相当于增加船舶的侧面积，使船舶的稳定性得到增强。