新型拍动翼仿生推进性能

徐令令， 李永成

(中国船舶科学研究中心, 江苏 无锡 214082)

0 引 言

近年来，随着小型仿生无人航行器和无人潜器的迅猛发展，人们开始将注意力转向自然界，尝试从自然界中找到一种能用来指导新产品研发的一般规律[1-2]，鱼的游动就是其中一种。鱼类具有较强的运动能力，如快速性、操纵性和推进性能等[3]。童秉刚等[4]根据鱼类在游动过程中身体变形部位占身体的比例，将鱼类的游动模式分为鳗鲡模式、鲹萪模式和月牙尾推进模式等3种。在这3种运动模式中，月牙尾推进模式最为常见，该模式对应的身体运动可抽象为升沉运动与俯仰运动的耦合运动，即拍动运动。

关于鱼类的拍动运动，国内外相关学者已开展大量研究工作。童秉刚等[4]提出采用波动板理论数值模拟鱼类的游动过程；SHAO等[5-6]提出一种改进的浸没边界法，对低雷诺数下的鱼游运动进行数值模拟研究；WU等[7]对考虑壁面效应的鱼类游动进行数值求解，结合推进效率和鱼体周围的流场结构确立最佳壁面距离；MA等[8]采用重叠网格技术对考虑侧壁面效应的三维鱼类拍动运动进行数值求解，确立最佳壁面距离。

上述对拍动运动的研究主要是基于简化的数学模型，将鱼类的俯仰运动简化为一个标准的正弦函数或余弦函数进行的。然而，鱼类的游动并非如此“标准”，本文选取新的运动函数来描述鱼类的运动，以最大程度地反映鱼类的真实运动。基于重叠网格理论对“非标准正弦”运动的拍动翼的推进特性进行数值模拟，从运动机理上对海洋生物游动的高机动性和高效性进行解释，以便设计出推进性能、机动性能和低噪声特性均较优的仿生拍动翼，为新型自主式水下潜器(Autonomous Underwater Vehicle, AUV)的研发提供参考。

1 计算模型和运动方程

本文选取二维的NACA0012翼型作为计算模型，弦长为1 m，机翼放置在2个平行的壁面中间，入口边界和上下边界均设置为速度入口边界条件，出口边界设置为无回流边界条件(见图1)。

机翼的拍动运动包含2个方向的运动，分别为竖直方向的升沉运动和绕着自身旋转的旋转运动。拍动翼运动过程示意见图2。

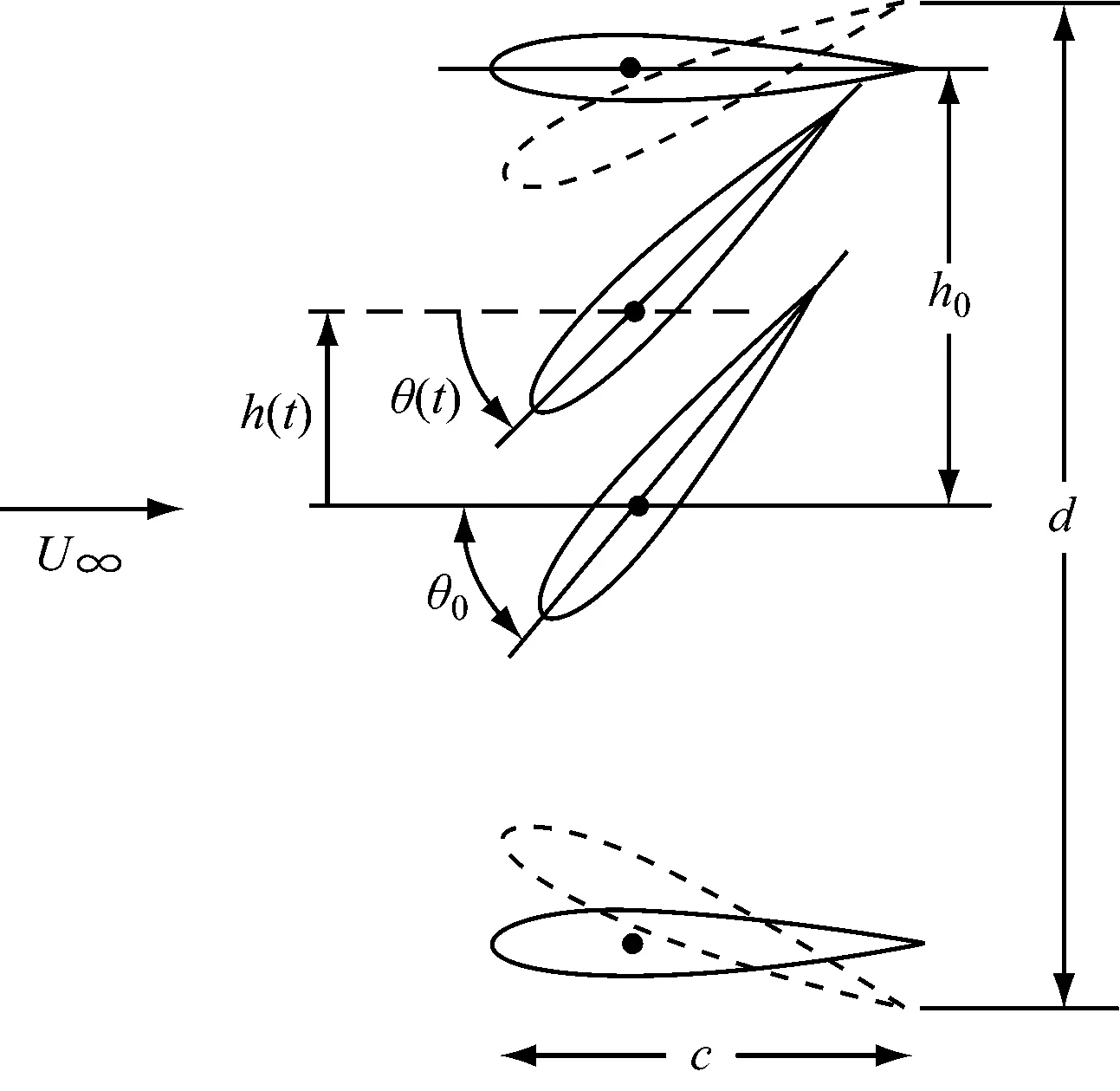
图2 拍动翼运动过程示意

与已有研究类似，升沉运动仍选取为简谐运动，而俯仰运动选取为非简谐运动，二者的运动周期一致，但存在相位差。运动方程为

h(t)=h0sin(2πωt)

(1)

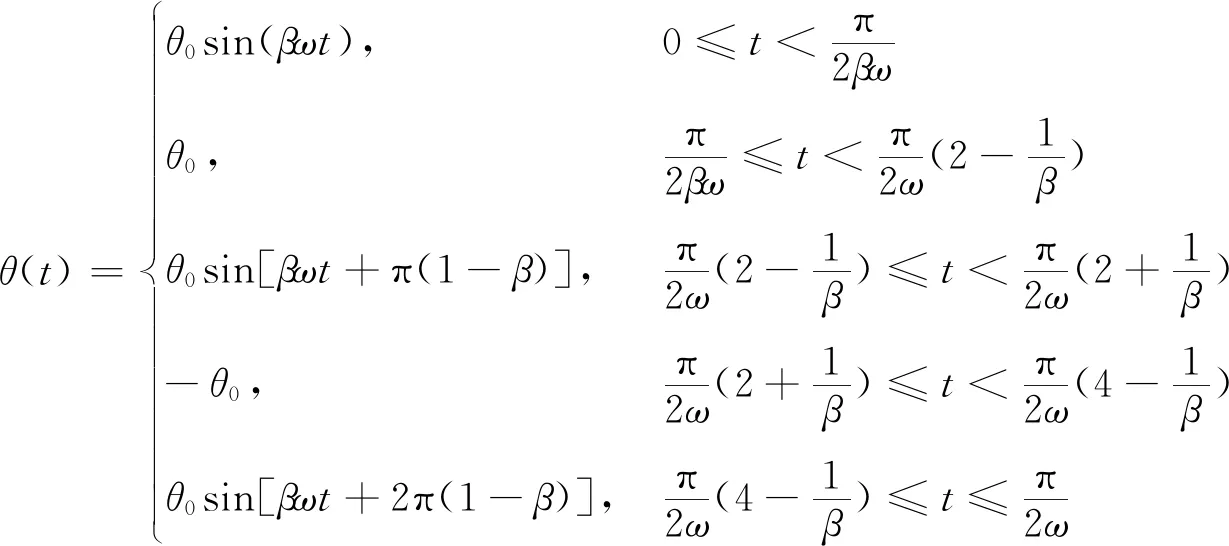
(2)

式(1)和式(2)中：h0和θ0分别为升沉振幅和俯仰振幅；ω为拍动频率；β为常数，本文取β= 1.0，1.5，2.0和4.0。

为更直观地描述机翼的俯仰运动，对机翼在一个周期内的运动过程进行分析(见图3)，其中：T为运动周期；θ0设置为30°。由图3可知:在不同β值下,拍动翼俯仰角呈锯齿形变化;随着β值的减小，拍动翼俯仰角的变化曲线接近于正弦曲线。

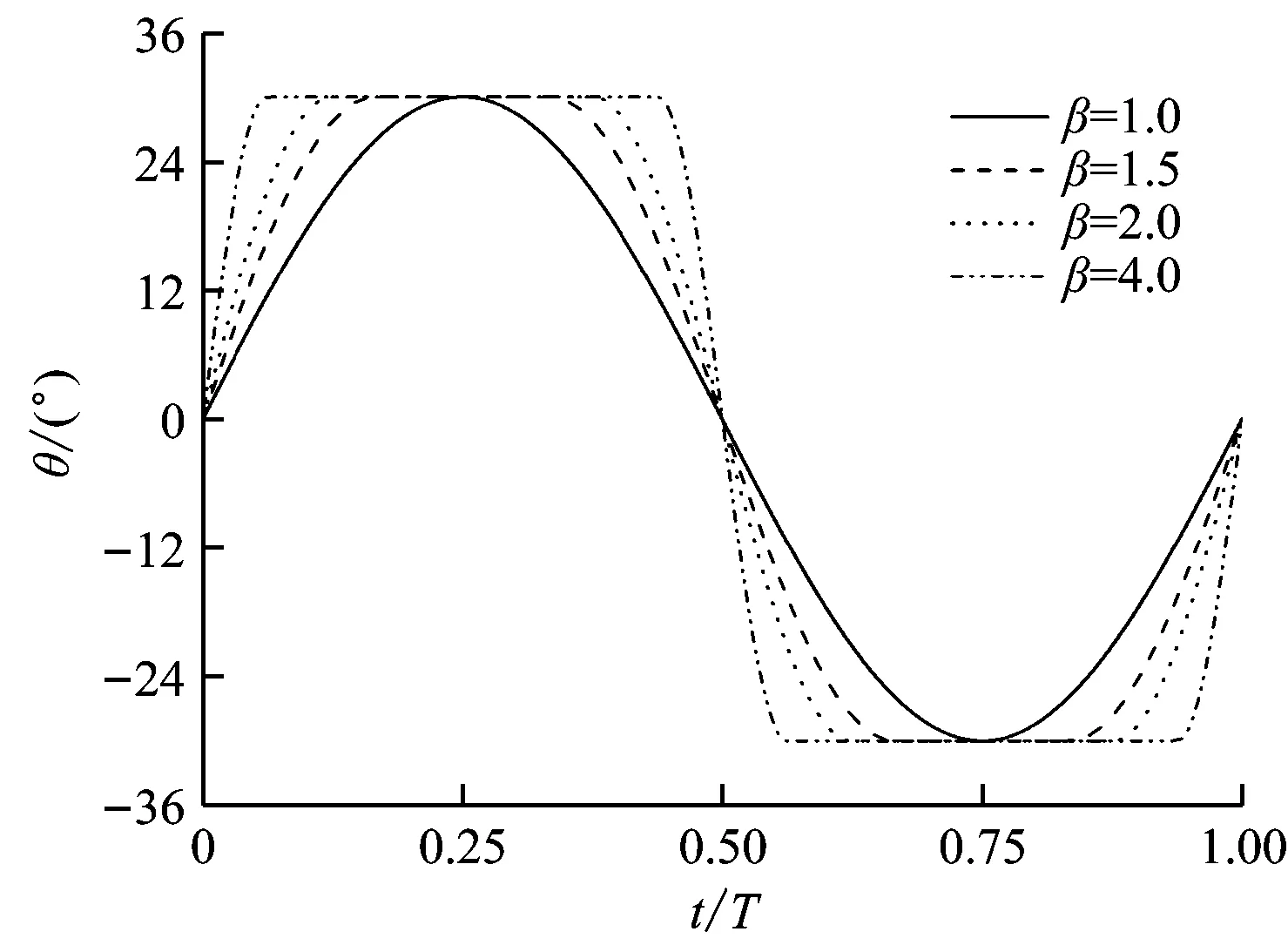
图3 不同β值下拍动翼俯仰角随时间的变化曲线

2 数值方法

本文研究的拍动翼问题属于典型的黏性不可压缩流场求解问题，因此需求解N-S方程。控制方程为

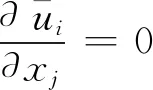
(3)

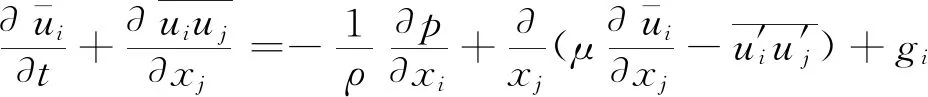
(4)

本文主要借助商业软件ANSYS 17.2中新增的重叠网格功能对拍动翼进行数值求解(重叠网格理论的详细介绍见文献[9]和文献[10])。在研究拍动翼问题时，需对2套网格进行数值模拟。拍动翼周围被椭圆状网格包裹的网格称为重叠网格(见图4a)，该部分网格进行拍动运动；计算域网格称为背景网格(见图4b)，该部分网格静止不动；2套网格的重叠区域进行数据交换。为保证数值计算的精度，采用结构化网格进行计算。取机翼弦长C为特征长度，二维计算区域的大小为40C×25C。机翼周围第一层网格的高度为1(即y+=1)，确保其位于黏性底层区域，网格总数约为9.2万个，数值计算方法的精度验证可参考已有研究进行。

a) 重叠网格

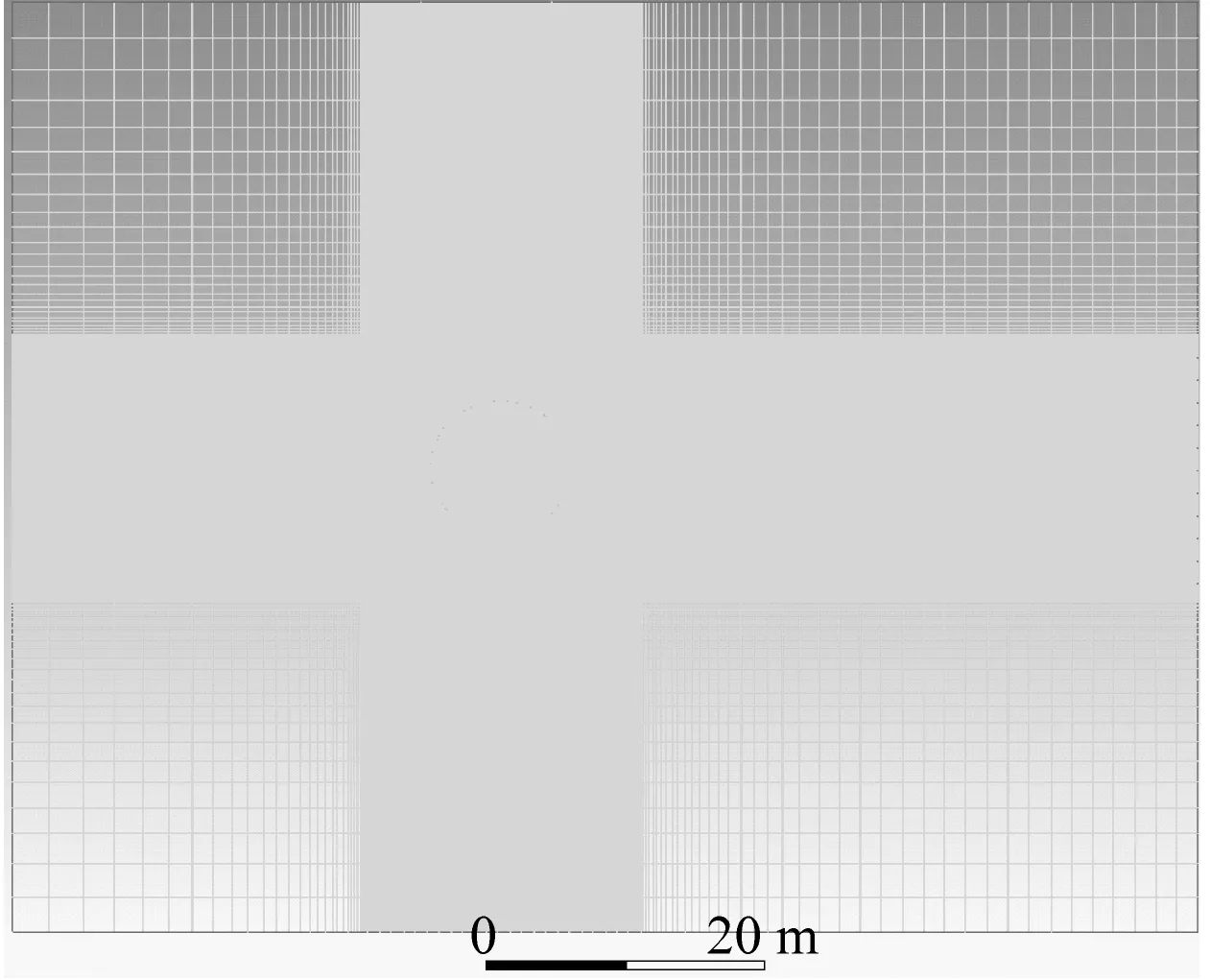
b) 背景网格

c)组合网格

图4 机翼表面网格和机翼头部网格示意

3 结果与讨论

针对拍动翼模型，采用商业软件Fluent对拍动翼在不同β值下的流场进行数值模拟，并系统地考察拍动翼的俯仰运动幅值和斯特哈尔数对拍动翼推进特性的影响。斯特哈尔数为拍动翼研究中较为常见的无量纲参数，其数学表达式为St=2h0f/U0。该无量纲参数融合了升沉运动幅值、拍动频率和来流速度等运动参数，可较为客观地评价拍动翼的推进性能。

3.1 俯仰运动幅值对拍动翼推进特性的影响

图5为不同β值下拍动翼推力系数和推进效率随俯仰运动幅值的变化曲线，俯仰运动幅值的变化范围为10°～50°，其他参数保持不变，分别为：h0=0.5C；f=0.3 Hz；St=0.30。推力系数CT和推进效率η的定义分别为

(5)

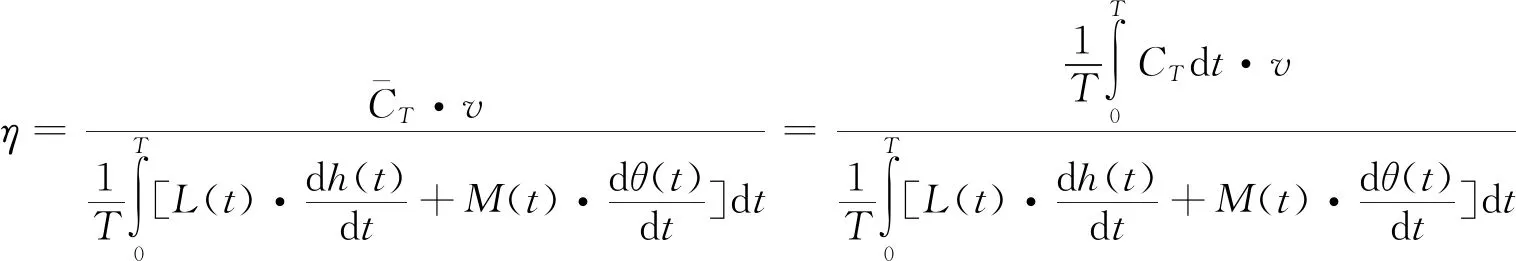
(6)

式(5)和式(6)中：T为拍动翼产生的推力；ρ为水的密度；v为来流速度；L(t)和M(t)分别为拍动翼垂直方向的升力和绕着转动中心的力矩。

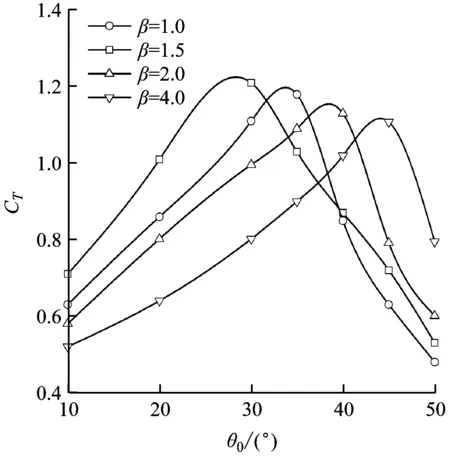
a) CT随θ0的变化曲线 b) η随θ0的变化曲线

由图5可知：在某一β值下，拍动翼产生的推力系数随着俯仰运动幅值的增大而先增大后减小，且存在最佳俯仰运动幅值对应最大推进力系数；在某一θ0值下，随着β值的增大，相应的推力系数先减小后增大，当β=1.5时推力系数达到最大。

此外，在某一β值下，拍动翼获得的推进效率随着θ0值的增大而逐渐增大，该结论与文献[11]中的结论相符。同样地，当β=1.5时，拍动翼获得的推进效率比另外三者高。因此，结合推力系数和推进效率，可认为β=1.5时拍动翼能获得较优的推进特性。

3.2 斯特哈尔数对拍动翼推进特性的影响

类似地，给出不同β值下拍动翼推力系数和推进效率随St的变化曲线(见图6)，拍动频率的变化范围为0.2～0.8，相应的St的变化范围为0.2～0.8，其他参数保持不变，分别为：h0=0.5C；θ0=30°；Ψ=90°。

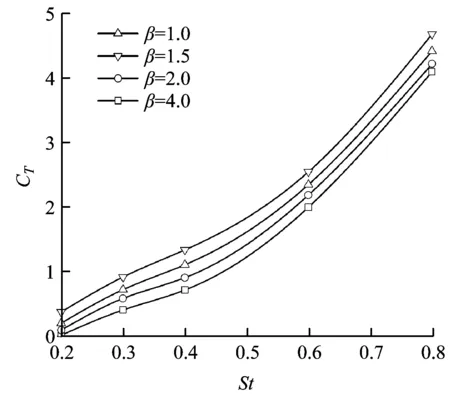
a) CT随St的变化曲线 b) η随St的变化曲线

由图6可知：在同一β值下，拍动翼推力系数随St的增大而逐渐增大，对应的推进效率增大到峰值之后逐渐减小，对应最大推进效率的St值随β值的增大而逐渐增大。具体地，当β值从1.0分别增加到1.5、2.0和4.0时，对应的最佳St值从0.35变为0.30、0.42和0.47。这就意味着在获得较大推力的同时，推进效率必然有所损失。因此，在后续设计仿生潜器时，需找到续航力与速度之间的平衡。

此外，在不同St下，拍动翼的推力系数和推进效率均在β=1.5时达到最大值。该结论与第3.1节的结论相吻合，再次说明β=1.5时拍动翼能获得最佳的推进性能。

4 结 语

本文基于重叠网格理论对拍动翼在不同β值下的推进运动进行数值模拟，详细分析不同β值下拍动翼的运动参数对拍动翼推进性能的影响。数值计算结果表明，β值对拍动翼的推进性能有重要影响。结合推力系数和推进效率值确立最佳值β=1.5。本文的研究成果可为后续仿生潜器的研制提供技术依据和理论指导。