例谈平面向量数量积几何意义的应用
2019-07-22 02:45浙江省诸暨荣怀学校黄敏诚
数学大世界 2019年14期
浙江省诸暨荣怀学校 黄敏诚
平面向量问题是近年来高考考查的热点也是难点,有关平面向量的命题也越来越灵活。向量问题通常有三种处理方法:坐标法、基向量法、几何法。而几何法具有直观性和简捷性的特点,同时它具有的灵活性也使得它不易被掌握,但用好向量的数量积的几何意义却能使很多问题的解决变得简单。
本题主要将数量积转化为向量投影问题,利用数量积的几何意义进行解题。
例2 (2018 年绍模)已知正三角形ABC 的边长为4,O 是平面ABC 上的动点,且则的最大值为
解析:主要考查平面向量的三角转化和数量积及其几何意义投影问题。

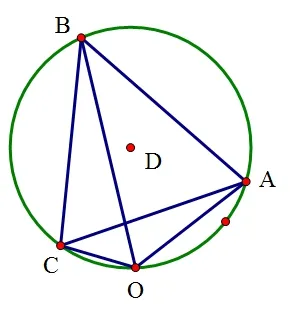


解析:主要考查平面向量的三角转化和数量积及其几何意义投影问题。



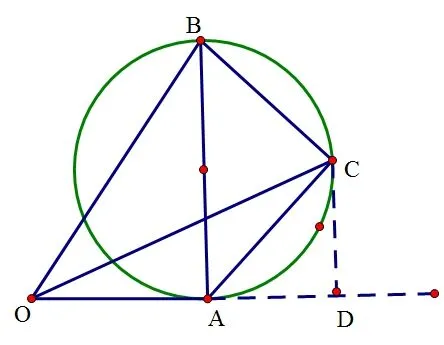
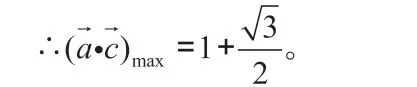


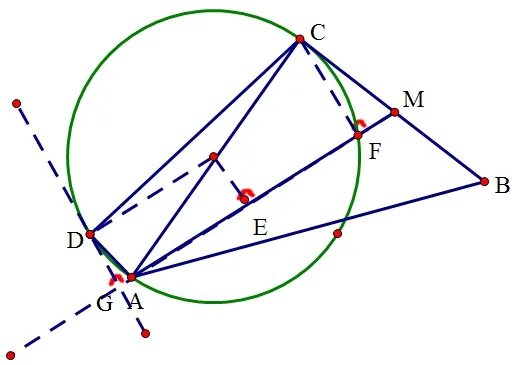


总之,平面向量关于数量积的问题,可以通过数形结合的思想,通过转化、结合向量的线性运算,根据数量积的几何意义(投影)来解决向量数量积问题,往往能使题目简单明了,通过数形结合的思想,能收到事半功倍的效果。
猜你喜欢
军事文摘(2022年8期)2022-05-25
中学生数理化·七年级数学人教版(2022年4期)2022-04-26
理科爱好者(教育教学版)(2022年1期)2022-04-14
新世纪智能(数学备考)(2021年5期)2021-07-28
中学生数理化·七年级数学人教版(2021年4期)2021-07-22
中学生数理化·中考版(2020年12期)2021-01-18
新疆大学学报(自然科学版)(中英文)(2020年2期)2020-07-25
中学生数理化·高三版(2019年1期)2019-07-03
学生天地·小学低年级版(2019年5期)2019-06-05
学生天地(2019年15期)2019-05-05

