探索性问题
山东省广饶县第一中学二校区 缪永春
探索性问题是相对于给出明确条件和结论的封闭性问题而言。探索性问题形式新颖、解法多样,需要灵活综合运用基础知识、基本技能和数学思想方法,它的主要形式体现在以下几种。
一、归纳型
例如:观察下列各式:
①tan10°tan20°+tan20°tan60°+tan60°tan10°=1,
②tan5°tan10°+tan10°tan75°+tan75°tan5°=1。
分析上述各式的共同特点,写出能反映一般规律的等式,并证明你的结论。
分析:分别对两式进行整理,tan10°tan20°+tan60°(tan20°+tan10°)=1,tan5°tan10°+tan75°(tan10°+tan5°)=1,由此可以看出具有两角和的正切函数的特点,并且30°+60°=90°,75°+15°=90°,据此可得出相应的等式。
点评:解决这类问题关键是对于所学的公式及变形要有熟练的掌握程度,同时要对题目中相关的内容进行有效的整理并能发现其特点。
二、存在型
分析:本题主要考查一元二次函数在闭区间上的值域的求法,关键在于正确分清一元二次函数的对称轴和区间的位置关系,确定函数的单调性求值域。
点评:本题利用函数的最值确定了对称轴和区间的关系,使问题变得简单。同时,解决存在型问题要注意以下三点:一是认真审题,明确目的。二是善于挖掘隐含条件,提高准确性。三是开阔思路,因题定法。
三、类比推理型
分析:首先利用综合法证明结论正确,然后依据直角三角形与四面体之间形状的对比猜想结论,并予以证明。
解:如图1 所示,由射影定理知,AD2=BD·DC,AB2=BD·BC,AC2=BC·DC,

图1
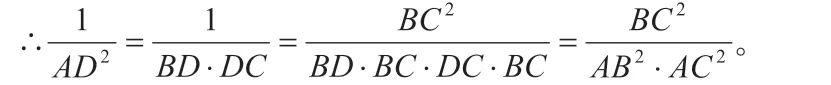



图2
∴猜想正确。
点评:类比推理是根据两个对象有一部分属性类比推出这两个对象及其属性为类似的一种推理方法。
四、条件探索型
分析:要证明线线垂直,往往需要转化为线面垂直来进行证明。

图3
点评:这类问题的解决需要添加的条件并不是唯一的,我们可以将结论当作已知条件,寻找能使该结论成立的条件,使得问题成立。

