标签带噪声数据的重加权半监督分类方法
陈 倩,杨 旻,魏鹏飞
(烟台大学数学与信息科学学院,山东 烟台 264005)

定义标签噪声为:
其中ρ+1,ρ-1∈[0,1)且ρ+1+ρ-1<1.
目前,许多分类器的设计都是通过带有标签的数据训练得到的,分类的准确性依赖于数据标签的准确性.但实际应用中,由于种种原因,数据标签经常被损坏,如何从带有噪声标签的数据中获得分类器引起科研工程人员的广泛关注.在全监督学习的框架下,ANGLUIN和LAIRD[1]提出了随机分类噪声(RCN)模型,其中每个数据标签以概率P∈[0,0.5)独立翻转;ASLAM和DECATUR[2]证明,如果函数类是有限的VC维度,利用0-1损失函数的RCN是PAC可学习的;KEARNS[3]还提出了学习RCN的统计查询模型,FRENAY和VERLEYSEN[4]针对不同类型的标签噪声带来的后果进行了研究;SCOTT[5]通过“混合比例估计”给出了一种基于代理风险最小化的存在噪声标签的分类算法,LIU等[6]在此基础上做了进一步改进,提出重要性重加权的方法.
然而,对所有数据进行标记往往费时费力,甚至很难完成,很多实际应用中,往往只能得到小部分带标签数据.为此,本文将研究一部分数据标签缺失,且标签又有噪声的分类问题.我们着眼于二分类问题,主要步骤及思路如下:首先,利用已标注数据,采用密度估计方法评估标签的重要性,建立带权的优化目标函数,从而得到初始分类器;其次,用训练好的分类器分类无标签数据,将置信度较高的一部分数据移入训练集中;然后,再次进行重加权分类,得到新的分类器.重复上述过程,直到所有数据均已处理.
本文主要创新改进之处在于:第一,针对的数据集仅有部分数据带标签且标签带有噪声,解决了标注数据有限且带噪声的情况下分类的准确性,节约了大量的标注成本;第二,引入相对无约束最小二乘重要性拟合(RULSIF)算法[7]代替文献[8]中采用的Kullback-Leibler重要性估计(KLIEP)算法进行标签重要性的估计,方法具有更好的准确率.数值实验表明,在典型数据集上本文提出的重加权半监督方法获得了与文献[8]提出的全监督方法相媲美的分类表现.
本文主要结构如下:第1节介绍重要性重加权的基本概念以及条件概率密度估计方法;第2节建立重要性重加权的半监督分类方法;第3节在部分典型数据集上,进行数值实验,在不同噪声率下给出了与全监督方法的比对结果.
1 重加权优化目标
本节主要介绍全监督情形下标签带噪声数据分类优化方法.首先考虑分类的期望风险

实际应用中用经验风险近似期望风险,故最优分类器可由下述重加权优化问题获得:
其中F是给定函数类.
文献[6]证明了如下2个结论,并将其用于权重的计算.
定理1[6]噪声样本的权重满足下述关系:
(1)
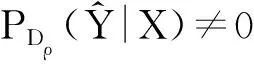
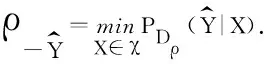


注意到该估计方法往往需要一定的先验知识,并且对数据的适应能力有局限性.

当样本数量足够大且维度较低时,可用带窗的核密度(例如高斯核函数)分别估计右端的3个概率.但是,这一密度估计方法在高维情况下效果欠佳,且需要大量的计算时间和存储量,由于分别计算了3个概率密度,故误差比较大.
(c) 密度比估计方法
c.1KLIEP算法[8]
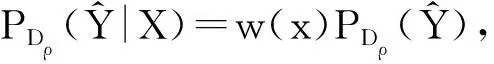
c.2RULSIF算法[7,12]
对c.1中的w(x),通过最小化如下γ相关PE散度求解:
其中γ为相关密度比,0≤γ≤1.进一步,记γ相关密度比
RULSIF算法采用Gauss核函数拟合
其中,θ=[θ2,θ2,…,θn]是待求的向量参数,σ是核宽度.最后通过最小化平方损失来求得θ.
密度比估计方法虽然需要求解额外的优化问题,但适用于高维数据,精度高于概率分类方法和核密度估计方法.本文的实验将采用RULSIF算法,相比KLIEP算法,RULSIF在我们的实验中对噪声率的估计具有更好的准确性.
2 半监督重加权分类
实际问题中由于代价、风险等多种原因,很难获得所有数据的标签,半监督学习[13]是近年来机器学习研究领域的一个热点.相对于有监督学习(只使用有标签数据训练)和无监督学习(只使用无标签数据训练),半监督学习应用少量带标签数据和大量无标签数据训练分类器,大大减少了人工标注代价,提高分类器性能.半监督学习解决了2个问题,一个是利用现有数据模拟出真实数据在特征空间的分布特点,二是在此基础上确定分类边界.
在半监督分类研究方面,self-training[14]算法的学习过程用少部分有标签的数据来训练初始分类器,然后用训练好的初始分类器分类无标签数据,将置信度比较高的一部分数据移入训练集中,然后再用新的有标签数据集重新训练分类器并再次分类无标签数据,不断循环,直至训练出的模型符合要求.其中挑选置信度高的数据移入训练集是基于类概率估计,若属于某类的概率超过预定义阈值T,则为该数据分配标签.
在有限数据带标签且标签带有噪声的前提下,我们将结合self-training和重要性重加权提出半监督重要性重加权算法.该算法基于数据具有连续性假设,即特征空间相互靠近的点的标签相同的概率比较大.
算法的主要思路是首先用已知标签数据结合重要性重加权,建立带权的优化目标函数,得到初始分类器;然后利用初始分类器分类未带标签数据,每个缺失标签数据得到标签后,我们将输出类别概率较高的数据加入训练集中;接着,用新得到的训练集再进行重加权分类,得到新的分类器.上述过程不断重复,直至所有数据都打上标签或是达到我们提前设置的循环次数,算法即停止,输出最优分类器.接下来给出具体算法.
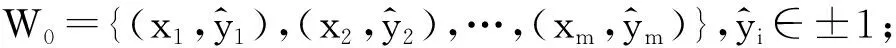
半监督重要性重加权分类算法:
1) 初始化:令k=0,给定最大迭代次数Nmax,给定删选阈值T;
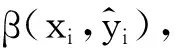

4) 若Hk+1≠∅并且k 上述算法中删选阈值T主要用于将置信度高的数据加入训练集中,进而更新分类器,T的取值范围一般在0.7与0.9之间,而Nmax是为了控制半监督循环次数. 本文实验的运行环境为:系统Ubuntu 16.04,CPU i5-7500,频率3.4 GHz,内存12 GB,Python 3.5,Pytorch 0.4.0.实验数据采用UCI医学分类数据集[15].实验中采用的优化求解器为BP神经网络,我们选用sigmoid函数作为神经元的激活函数,最后的输出经softmax函数变换后属于(0,1),表示该数据属于某个类别的概率. 实验中每组数据都按比例7∶3分成训练集和测试集,训练集中随机删去部分数据的标签,而保留的标签又根据给定噪声率ρ+,ρ-随机翻转,损失函数采用均方损失,利用BP网络进行分类训练,设置类别的删选概率阈值T=0.865,最大迭代次数Nmax=103.为了避免偏差,每组实验进行5次,分类准确率取5次实验结果的平均准确率作为最后的分类准确率. 表1—表3为不同数据集上的运行结果,其中第一行表示带标签数据占整体数据的百分比(m/n),第一列表示噪声率. 表1 在THYROID数据集上的分类准确率 表1为THYROID数据集结果,特征维度5,样本量215个,含正例65个,负例150个. 表2 在HEART数据集上的分类准确率 表2为HEART数据集结果,特征维度13,样本量270个,含正例120个,负例150个. 表3 在GERMAN数据集上的分类准确率 表3为GERMAN数据集结果,特征维度20,样本量1 000个,含正例300个,负例700个. 通过表1-表3可发现:(1)分类准确率随着数据维度的增加而逐渐降低,5维数据最高的分类准确率高达85%以上,而在20维数据上最高的准确率只有73.33%,这主要是因为特征维度的提高影响了权重估计的准确性;(2)分类准确率随着噪声率的提高而降低.(3)标签数据比例为80%,50%的情况下,半监督的分类准确率与全监督接近,特别地,表3中噪声率(ρ+=0.4,ρ-=0.4)时,50%对应的半监督准确率高于全监督,这一现象可能的原因是被保留标签的50%数据恰巧具有更好的可分性,而这些好的可分性在随后的多次循环过程中得以累计,从而导致最后的准确率提升. 本节的实验结果表明本文提出的方法在样本数据质量较差(标签不足且受损)的情况下,仍然取得了较好的分类准确率.在未来的研究中可进一步考虑:(1)将方法推广至多类问题;(2)标签带噪声的不完整数据的分类问题.3 实验及结果分析