恒压变量斜轴泵联合仿真模型及特性分析

(太原理工大学 新型传感器与智能控制教育部和山西省重点实验室，山西 太原 030024)

引言

恒压斜轴泵具有压力高、排量大、容积效率高、自吸效果好的优点，其输出压力可与负载相匹配，对工程机械节能具有很大意义。许多学者对变量柱塞泵的特性进行了研究，BAEK等[1]研究了斜轴式柱塞泵的理论机制，通过几何方法研究了活塞的倾斜角对泵性能的影响。PARK等[2]设计出一种鲁棒压力控制策略，实现了变量斜轴泵压力和流量的精确控制，试验验证了该方法的准确性。HONG等[3]研究了斜轴式柱塞泵的摩擦损失，获得了影响扭矩的因素。通过试验验证了活塞运动方程和泵部件的理论摩擦模型，并在此基础上，通过理论公式获得了泵的摩擦力矩。文哲[4]对恒压控制的数字泵特性进行了研究，与常规恒压泵相比，负载变化引起的泵出口压力变化小。张宏[5]采用AMESim建立了恒压泵液压模型，分析了负载阶跃条件下仿真曲线，仿真结果表明：泵输出压力脉动主要受压力控制阀阀芯直径和行程缸活塞直径影响。罗威等[6]采用AMESim建立了恒压变量泵模型，对动静态特性进行了分析，通过对比样本曲线，验证了模型准确性，并得到了泵超调量与恒压调整时间。黄鸣辉等[7]采用Simulink搭建电液比例柱塞泵的变量控制模型，同时采用阶跃信号为输入，分别进行流量动采用阶跃信号为输入，分别进行流量动态特性仿真和压力动态特性仿真，分析了三种不同配流窗口对系统动态性能的影响并比较了它们各自的优缺点。秦二卫[8]采用数学模型分析了恒压变量泵动静态特性分析，利用Simulink进行建模仿真，并且利用试验验证了模型的准确性。权凌霄等[9]用AMESim、ADAMS分别建立了斜轴泵液压、动力学模型，通过数据调用创立协同仿真平台，分析了阀芯阻尼、复位弹簧对变量机构控制特性的影响。郜立焕等[10]改进了恒压泵变量机构，采用Simulik建立泵变量机构数学模型，结果表明：对变量机构的改进达到了节能效果。张婉茹等[11]采用Simulik建立非对称变量泵模型，仿真分析了活塞直径、负载压力对泵动态特性的影响，结果表明：活塞直径越小，泵响应越快，负载压力增大可提高泵响应稳定性。王慧等[12]采用AMESim建立压力流量控制变量泵模型，仿真分析了换向阀参数对泵输出压力特性的影响，结果表明：减小阀芯质量、增大阻尼孔孔径可减小输出压力超调。

上述对斜轴式柱塞泵的研究均采用数学模型、液压仿真模型或机械仿真模型，无法同时对泵的液压特性和机械特性进行分析。为此，本研究提出一种斜轴式变量柱塞泵的机械液压联合仿真模型，对恒压泵动静态特性进行了仿真研究，得到了理想的控制效果曲线，为进一步研究高性能液压原件提供了理论指导。

1 恒压斜轴变量泵工作原理

1.1 斜轴泵结构示意图

斜轴恒压变量柱塞泵机械结构如图1所示，主要包括泵体组件、变量活塞组件、压力阀组件。缸体既受主轴驱动作绕自身轴线转动，又受变量活塞推动进行上下摆动，缸体摆动引起柱塞运动行程发生改变，液压泵排量发生改变。

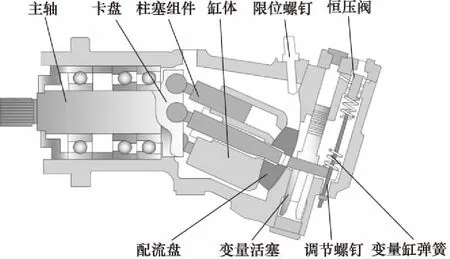
图1 斜轴泵结构示意图

1.2 恒压泵变量方式

斜轴式恒压变量泵变量工作原理如图2所示，控制单元主要由先导溢流阀、压力阀、阻尼孔组成。

图2 电液比例变量泵原理

当泵出口压力小于先导阀设定值时，压力阀左右两腔压力相等，弹簧力将压力阀推向右位，变量缸无杆腔排油，使得液压缸处于最大排量位置。当泵出口压力超过先导阀设定值时，先导阀开启，由于阻尼1的节流作用，压力阀两腔产生压力差，将压力阀阀芯推向左位，液压缸无杆腔压力升高，推动缸体摆角减小，液压泵排量减小，出口压力下降到设定值。

2 配流盘数学模型

斜轴泵缸体底部配流窗口与配流盘吸排油窗口形成的过流面积是液压泵输出流量压力脉动特性的主要参数之一，过流面积随着缸体转动而发生变化，以吸油面积为例，其过流面积可分为7个阶段如图3所示。

1) 进入三角槽(0<φ<φ1max)

根据几何关系可以推出，进入三角槽阶段的过流面积为：

S1(φ)=(Rφ)tanθ1sinθ1tanθ2/2

(1)

式中，S1——进入三角槽阶段过流面积，以此类推

R——三角槽所在圆半径

φ——柱塞转角(自上死点起始)

θ1——吸油口入口三角槽深度角

θ2——吸油口入口三角槽宽度角

φ1max——三角槽末端与上死点弧线所对圆心角

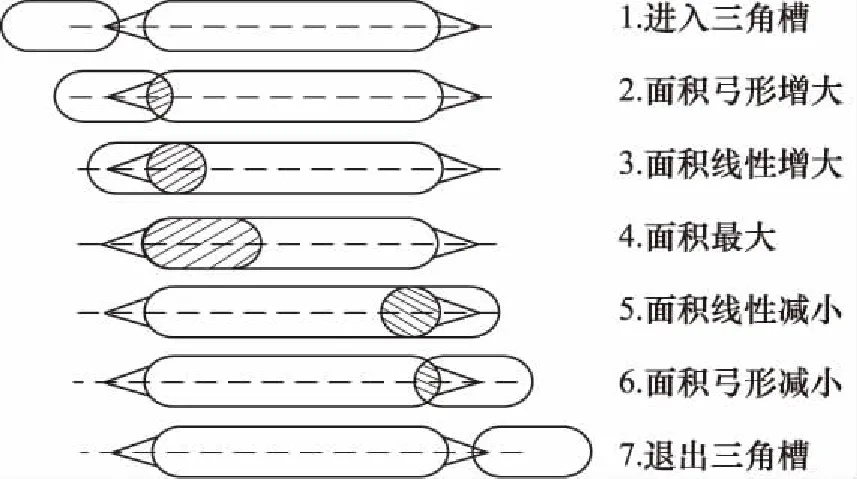
图3 配流盘面积计算

2) 面积弓形增大(φ1max<φ<φ2max)

由图3可知，此时缸体底部单个配流窗口与配流盘腰形槽半圆部分形成重叠，故过流面积为三角槽最大过流面积加上重叠面积。公式为：

S2(φ)=2(r2arccos(1-R(φ-φ1max)))-

sin(arccos(1-R(φ-φ1max)/2r))r(r-

R(φ-φ1max)/2)+S1(φ1max)

(2)

式中，S2——进入面积弓形增大阶段过流面积

r——配流窗口半圆端半径

φ2max——腰形槽半圆末端与上死点弧线所对圆心角

3) 面积线性增大(φ2max<φ<φ3max)

此时缸体底部单个配流窗口已经越过半圆面积，另一边还未退出三角槽，故过流面积公式为：

S3(φ)=πr2+2r(φ-2Δα-φ1max)R+S1(φ1max)

(3)

式中，S3——进入面积线性增大阶段过流面积

φ3max——配流窗口完全进入腰形槽时半圆末端与上死点弧线所对应圆心角

4) 面积最大(φ3max<φ<φ4max)

由图3可知，此时缸体底部单个窗口完全进入腰型槽，过流面积即为单个配流窗口的面积，公式为:

S4(φ)=πr2+2r(φ3max-2Δα-φ1max)R

(4)

式中，S4——进入面积最大阶段过流面积

φ4max——腰形槽矩形末端与上死点弧线所对应圆心角

5) 面积线性减小(φ4max<φ<φ5max)

S5(φ)=φr2+2r(φ4max-(φ-α)-

2Δα)R+S7(φ5max)

(5)

式中，S5——进入面积线性减小阶段过流面积

φ5max——腰形槽矩形末端与上死点弧线对应过流面积以及配流窗口所对圆心角之和

6) 面积弓形减小(φ5max<φ<φ6max)

S6(φ)=2(r2arccos(1-R(φ4max-φ+Δα)))-

sin(arccos(1-R(φ4max-φ+Δα)/2r))×

r(r-R(φ4max-φ+Δα)/2)+S7(φ6max)

(6)

φ6max——腰形槽半圆末端与上死点弧线对应过流面积以及配流窗口所对圆心角之和

7) 退出三角槽(φ6max<φ<φ7max)

S7(φ)=(R(φ7max-φ))2tanθ3sinθ3tanθ4/2

(7)

式中，S7——退出三角槽阶段过流面积

φ7max——三角槽末端与上死点弧线对应圆心角以及配流窗口所对应圆心角之和

θ3——吸油口出口三角槽深度角

θ4——吸油口出口三角槽宽度角

根据式(1)～式(7)可类推单个柱塞配流窗口在排油窗口的过流面积变化公式。将上述公式编辑到单个柱塞模型单元中，得到单个柱塞吸排油口过流面积变化仿真曲线如图4所示。可知，吸排油口面积变化与上述七个阶段一致，吸排面积会有部分重叠，因为吸油口未完全关闭时，排油口已打开。

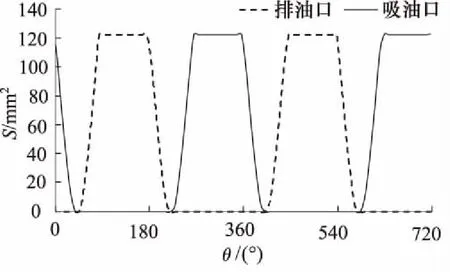
图4 吸排油口过流面积

3 恒压斜轴泵建模及仿真

3.1 恒压斜轴泵建模

在多学科仿真软件SimulationX中建立变量泵如图5所示，模型主要包括油源、压力阀、节流阀、溢流阀、卡盘、缸体、柱塞组件及变量组件。卡盘与柱塞、柱塞与柱塞套采用球绞副连接，柱塞与柱塞套用滑动副连接；缸体与变量机构用约束模型限制，既能实现缸体自转，也能实现缸体上下摆动。

历史是在事情出了差错的地方开始的；历史只和麻烦、困惑、悔恨共生。因此紧跟在“为什么”这个词之后的，就是狡猾又充满希冀的字眼“假如”。若非因为……只要……要不是……这些历史中无用的“假如”。而不断阻止、偏离、转移对“为什么”这一问题的追溯，则显出另一种形式的退步：要是我们能回到过去该多好。要是我们能重新开始。要是我们能回到……[2]90-91

图5 斜轴泵机械液压联合仿真模型

采用二位四通阀和一个闭式容腔来模拟二位三通压力阀阀套，用单位质量块模拟阀芯质量，阀芯连接端位止动装置模型限制阀芯位移，端位止动装置模型遵守动量守恒定律，可以获得与之相连接质量块的位移、速度、损失功率。随后将Pro/E中建立的三维模型以stl格式导入仿真软件中。

3.2 流量压力脉动仿真分析

运用可变节流阀模拟负载。变量泵主轴转速为1200 r/min,液压泵排量55 mL/r，先导阀设定压力21 MPa，根据测绘设置液压泵仿真参数，如表1所示。

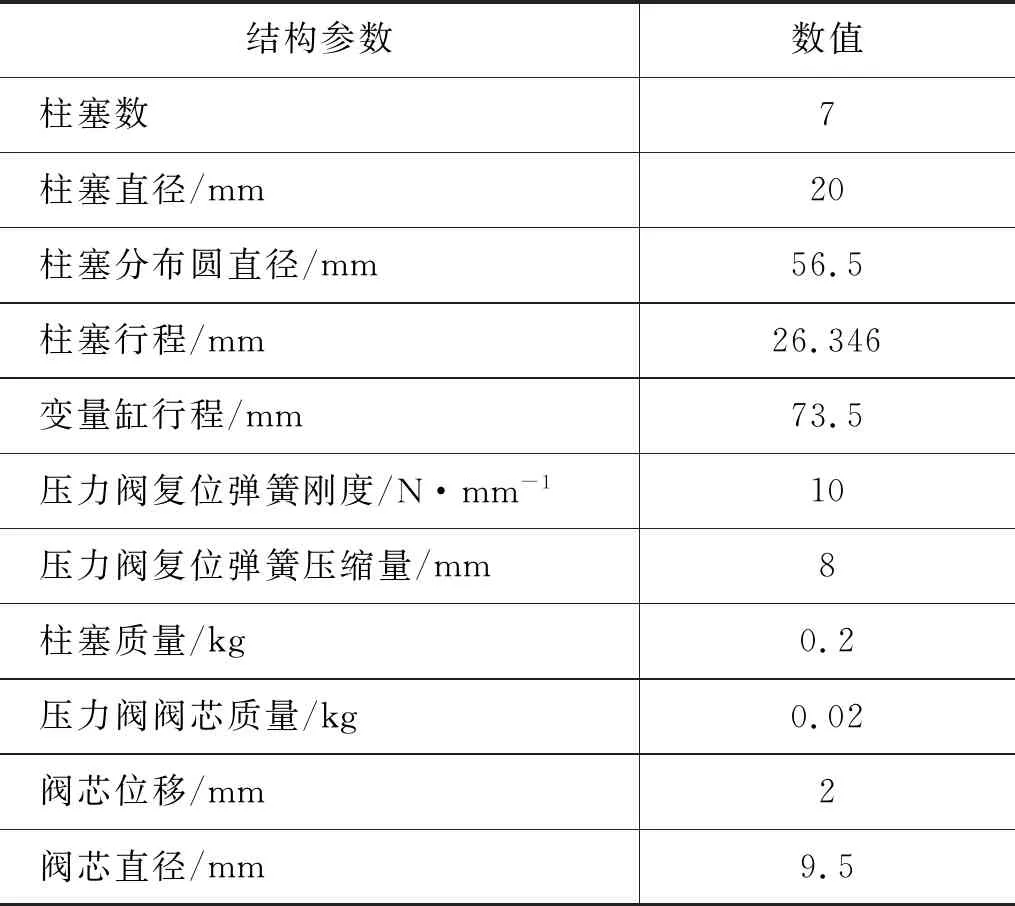
表1 液压泵仿真参数表

单柱塞流量随缸体转角变化曲线如图6所示，可知，单柱塞流量为正弦变化，与图4所示过流面积变化一致。

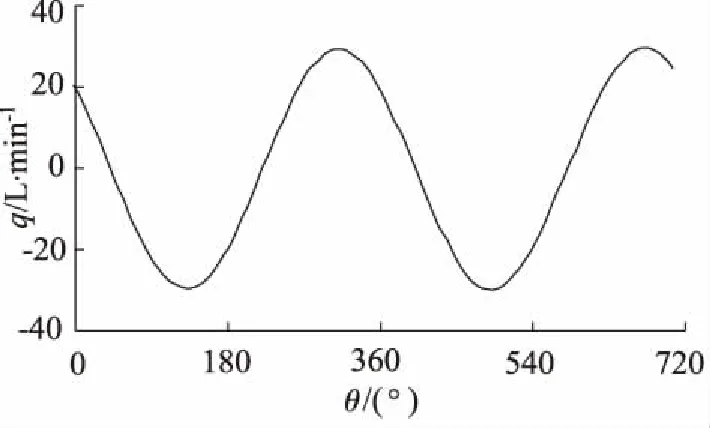
图6 单柱塞流量

单柱塞底部压力随缸体转角变化曲线如图7所示，可知，柱塞底部压力下降前会有正向超调，因为柱塞经过出口三角槽时，柱塞底部油液还处于压缩状态，而排油口已经关闭，导致压力产生超调。

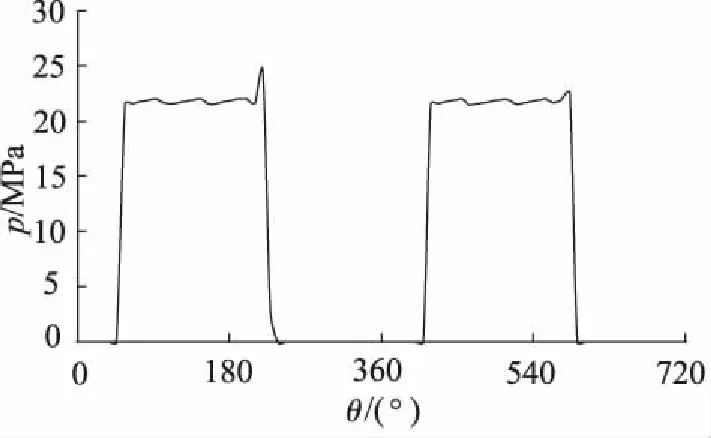
图7 单柱塞腔压力

单柱塞所受摩擦力随缸体转角变化曲线如图8所示，摩擦力与柱塞所受正压力以及摩擦系数有关，摩擦系数取决于机械结构及材料，所以摩擦力变化与单柱塞压力变化趋势一致。

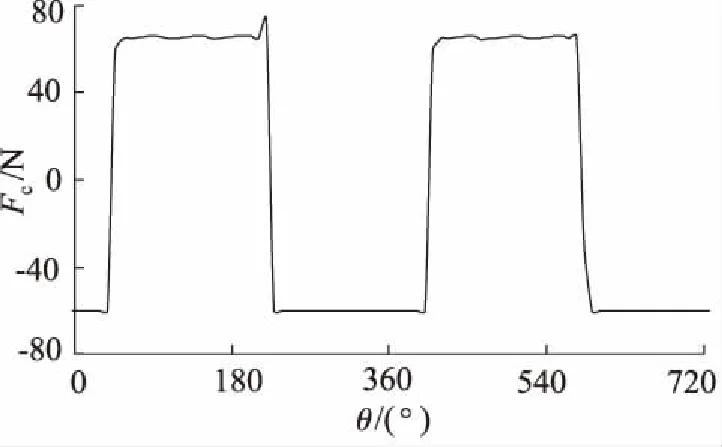
图8 单柱塞摩擦力

恒压斜轴泵输出流量与压力曲线如图9所示，泵输出流量由7个柱塞流量相互叠加，形成相对均匀总流量。输出流量脉动由两部分原因，一是柱塞正弦运动规律引起的流量脉动，二是吸排油口切换时压力变化引起的瞬时流量脉动。流量脉动必然引起压力脉动，由图可知，压力变化与流量变化一致。

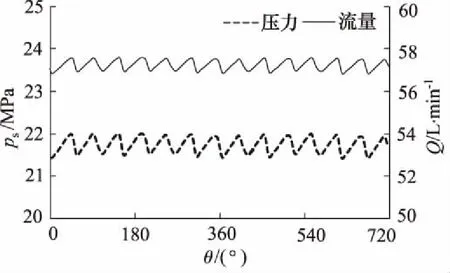
图9 泵输出流量与压力

3.3 静态工作特性

如图10所示为恒压泵静态仿真曲线，泵转速1800 r/min，溢流阀设定压力分别为12，15，18 MPa。由图中曲线可知，泵静态工作可分为两个阶段。最大排量阶段：理论上液压泵处于最大排量，但是随着泵出口压力升高(未达到先导阀设定压力)，泵泄漏增加，输出流量随压力增大缓慢减小。恒压控制阶段：输出流量与负载匹配，泵出口压力平均值分别为12.4，15.4，18.4 MPa，因为阻尼孔1的节流作用，致使阻尼孔1进出口产生压差，液压泵出口压力比先导阀设定值大。

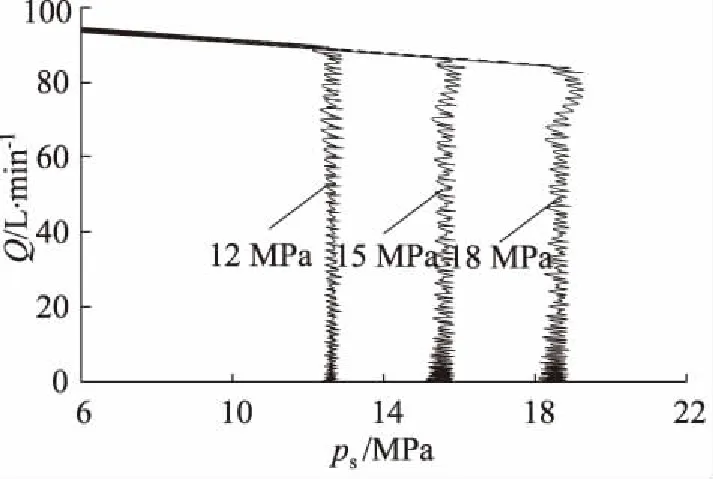
图10 恒压泵静态工作曲线

3.4 动态工作特性

先导溢流阀设定值20 MPa，泵转速1500 r/min，可变节流阀直径在1.5 s时由3 mm变为2 mm，得到恒压泵变负载工况下变量缸位移与阀芯位移曲线、输出压力与流量曲线、输入扭矩曲线分别如图11～图13所示。

图11 变负载工况变量缸位移与阀芯位移

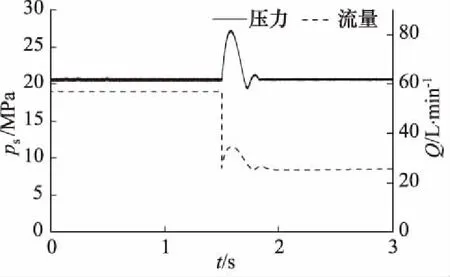
图12 变负载工况输出流量与压力

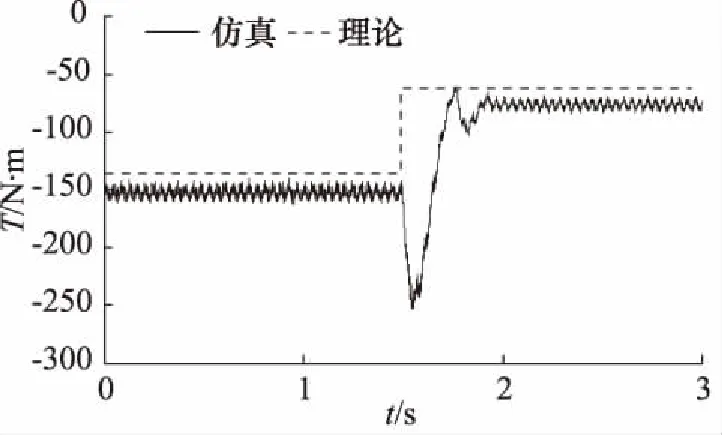
图13 变负载工况输入扭矩

由图11、图12曲线可知，液压泵输出稳定时，变负载前后，压力阀阀芯震荡区间右移(阀芯位移正、负值分别表示阀芯右、左位)，压力阀左端节流作用减小，无杆腔压力增加，变量缸活塞位置由57.3 mm变为28.1 mm，推动缸体摆角变小，恒压泵出口流量从54.8 L/min减小到24.5 L/min。液压泵出口压力变负载前后都稳定在20.4 MPa。

图13为恒压斜轴泵输入扭矩随时间变化曲线，根据能量守恒，有公式：

(8)

式中，T——输入扭矩

Δp——泵进出口压差

Q——泵出口流量

n——转速

恒压泵进出口压差恒定，主轴转速不变，根据式(8)理论计算与模型仿真得到泵输入转矩如图13所示，对比理论与仿真曲线可知，理论扭矩值与仿真值相吻合，存在的误差是忽略了容积损失与机械损失引起的，进一步验证了模型的准确性。

3.5 不同压力阀弹簧刚度对泵响应时间的影响

先导溢流阀设定压力17 MPa，恒压斜轴泵转速1200 r/min，变量缸复位弹簧刚度分别设置为65，50，35 N/mm，分别得到泵输出压力、流量曲线如图14、图15所示。可知，弹簧刚度越大，泵响应越快，当弹簧刚度为65 N/mm时，泵响应时间不再明显减小，响应时间为0.28 s。

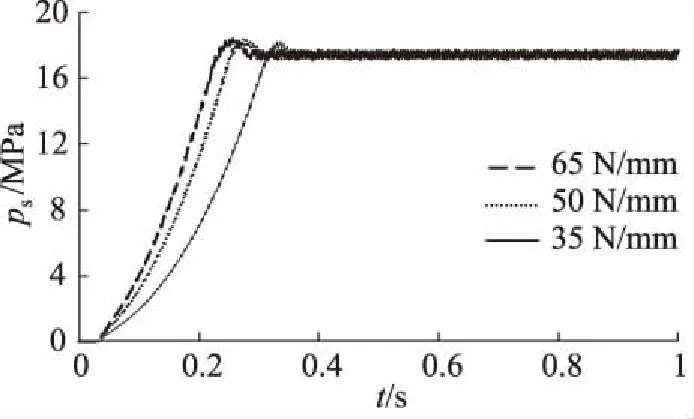
图14 不同变量缸弹簧刚度下泵出口压力

4 结论

(1) 建立了恒压泵的机械液压联合仿真模型，可同时对恒压泵的液压特性与机械特性进行分析；在理论分析的基础上，对恒压斜轴泵压力、流量、摩擦力、扭矩等特性进行了仿真分析，取得了良好的仿真结果；

(2) 仿真结果表明，采用远程压力控制，恒压泵具有良好的静动态特性，泵出口压力基本保持在先导溢流阀设定值；当负载突变时，压力超调小，响应时间短；

(3) 对比分析了变量缸弹簧刚度对泵响应时间的影响，结果表明，变量缸弹簧刚度越大，泵响应时间越短，当弹簧刚度增加到65 N/mm时，响应时间不再有明显缩短。