Heat transfer enhancement in magnetic and non-magnetic based nanofluid

College of Mathematics and Statistics, Shenzhen University, Shenzhen 518060, P.R.China

Abstract： A two-dimensional boundary layer steady flow of an electrically conducting nanofluid on a stretching sheet in the presence of a magnetic field is considered in this paper. The magnetic (Fe2O3) and non-magnetic (Cu) nanoparticles are used in water as a base fluid.The heat transfer process is sourced from the Newtonian heating boundary condition. The mathematical model of the flow is formulated by using a single-phase approach, which takes the nanofluid as a single homogeneous fluid.Under certain special condition for the existence of an exact solution, a system of governing nonlinear partial differential equations is reduced to a set of ordinary differential equations by using a suitable non-dimensional variable transformation.The Maple is used to obtain the exact solution in terms of the Whittaker function. We find that the nanofluid containing Cu nanoparticles has higher heat transfer rate than Fe2O3-water nanofluid.

Key words： viscous fluid mechanics; nanofluid; single-phase model; stretching sheet; Whittaker function; Newtonian heating

1 Introduction

A nanofluid is a suspension of metallic and non-metallic nanoparticles with dimension of less than 100 nm in the engineered colloidal liquids. Two decades ago, the concept of nanofluid was introduced by CHOI[1]to indicate engineered colloids composed of nanoparticles dispersed in a base fluid. The nanoparticles used in nanofluid are typically composed of metals, oxides, carbides or carbon nanotubes. Nanofluid possesses incredible thermo-physical properties, which do not exist in the convective heat transfer fluids, like water and organic fluids. The nanoparticles are relatively close to the molecules of the base fluid in size. Therefore, the suspension remains stable with little gravitational settling over a long time.Generally, mathematical modelling of nanofluid heat transfer flow can be classified as single-phase and two-phase models. In the single-phase approach, the combination of base fluid and nanoparticles is considered as a single-phase mixture with steady properties. By assuming negligible motion slip between the nanoparticles and the continuous phase, and the thermal equilibrium conditions also prevail, so the nanofluid may be then considered as a conventional single-phase fluid with effective thermo-physical properties. The single-phase model is very popular to study nanofluid behaviours numerically because of its simplicity. TIWARI et al.[2]used finite volume approach to study Cu-water nanofluid inside a two-sided heated square cavity. They concluded that the rate of heat transfer increased approximately 30% at 0.08 nanoparticles volume fraction. IZADI et al.[3]studied forced convection laminar flow of Al2O3-water nanofluid in an annulus by using single-phase model. The study of three types of nanofluids, namely, Cu, TiO2and Al2O3merged into water based fluid by using single-phase model was done by HADY et al.[4]. BAZDIDI-TEHRANI et al.[5]investigated mixed convection laminar flow of CuO-water and TiO2-water nanofluids inside a vertical rectangular channel by using single-phase model.Buoyancy induced flow of Cu-water nanofluid-filled eccentric annulus subject to a constant heat flux was investigated by HU et al.[6].MEHRYAN et al.[7]studied natural convection heat transfer through Fe3O4-water nanofluid in a square enclosure under the effect of entropy generation and horizontal periodic magnetic field numerically.

In the two-phase approach, the nanoparticles and the base fluid can be distinguished as two separated phases with different thermo-physical properties.DINARVAND et al.[8]performed a two-phase model simulation for double-diffusive mixed convection flow of a nanofluid under diffusiophoresis. SHEHZAD et al.[9]utilized the two-phase model to investigate nanofluid heat transfer convection in a wavy channel. KEFAYATI[10]examined the entropy generation on nanofluid flow in a porous cavity using two-phase mixture model.JAFARIMOGHADDAM[11]numerically investigated magnetic nanofluids over a stretching or shrinking wall. They used a two-phase mixture model to study the nanofluid thermal behaviour.SIDDIQA et al.[12]presented a two-phase dusty nanofluid free convection flow along a heated vertical wavy surface. Recently, a numerical study of hydrothermal analysis of boehmite alumina-water/ethylene glycol nanofluid in a minichannel heat exchanger was done by ALSARRAF et al.[13]. The nanofluid in the minichannel was assumed to be a two-phase mixture. Several other authors used the two-phase model in order to simulate heat transfer in nanofluids[14-18].

A porous medium is a continuous solid phase which having void spaces in it. The fraction of the void space to the total volume is named as porosity. Industrial and engineering applications of flows through the porous medium have attracted the attention of researchers. Purification and filtration processes, seepage of water in river beds, migration of pollutants into the soil and aquifers, drying of porous materials in textile industries, the movement of moisture through and under engineering structures, heat and mass transport in packed bed reactor columns are among the application and filtration of solids from liquids. “Flow is linearly dependent on the pressure gradient and the gravitational force” is known as Darcy Law. This law is generally accepted as the macroscopic equation of motion for the Newtonian fluids in porous media at small Reynolds numbers and when the medium is close-packed, i.e., it has a lower permeability.The peristaltic flow of Maxwell fluid with Hall and porous boundaries effects was investigated by KOMY et al.[19]. MEKHEIMER et al.[20]studied the effect of magnetic field and space porosity on the peristaltic motion of a Maxwell fluid in a confined parallel-plane microchannel. SHEREMET et al.[21]applied the two-phase model to study the double-diffusive mixed flow in a porous enclosure.ABDELSALAM et al.[22]studied the flow of Jeffrey fluid through a porous medium induced by a surface acoustic wave in a confined parallel-plane microchannel. Recently, ELMABOUD et al.[23]investigated electromagnetic flow through two regions. The first one is full of permeable matrix soaked in a Newtonian fluid and the second one has pure fluid.

The aim of the present work is to introduce a direct and effective method to obtain the analytical solution for steady two-dimensional flow of an electrically conducting nanofluid caused by a stretching sheet. Magnetic (Fe2O3) and non-magnetic (Cu) nanoparticles are considered in water as convectional based fluid. Newtonian heating condition has been applied to simulate the situation where the heat is transported to the convective fluid via a bounding surface which having finite heat capacity. The mathematical model is formulated base on a single-phase model. The thermal conductivity, heat capacity and viscosity are dependent on nanoparticles volume fraction.

2 Mathematical formulation

In the present study, an external uniform magnetic field is imposed on a nanofluid, and leads to an electromagnetic force due to the interaction of current with magnetic field. In the view of Ohm’s law, the current densityJis defined as

J=σNF(E+V×B)

(1)

whereEis the electric field intensity, which is neglected due to small magnetic Reynolds,Vis the velocity,Bis the magnetic flux intensity andσNFis the nanofluid electrical conductivity expressed as

(2)

In magneto-fluid mechanics, Maxwell’s equations are

(3)

whereμ0is the magnetic permeability. Finally, the electromagnetic forceFM is

(4)

Since the nanofluid is flowing through a porous medium, the Darcy’s law, which shows that the relationship between the pressure drop induced by the frictional drag and velocity, is

(5)

whereλis the permeability of porous medium andμNFis the effective dynamic viscosity of a nanofluid, given by BRINKMAN[24]as

(6)

The body forceFB per unit mass is

FB=ρNFg

(7)

The effective densityρNFof a nanofluid given by PAK et al.[25]

(8)

The steady 2D flow of nanofluids is considered through a porous medium. Thex-axis is taken in the direction of the sheet subject to Newtonian heating condition andy-axis is normal on it. Under these conditions, the flow is governed by the following equations

(9)

FM+FR+FB

(10)

(11)

All quantities and symbols are given in the nomenclature. The velocity field for 2D flows is defined as

V=[u(x,y),v(x,y),0]

(12)

After neglecting the pressure gradient and body forces, the continuity and motion equations in view of Eq.(4), Eq.(5) and Eq.(7) become

(13)

(14)

The total energy per unit volume which consists of internal energy and kinetic energy,can be expressed as

(15)

According to Ref.[26], the specific internal energyecan be expressed by using thermodynamic relation as

(16)

where (Cp)NFis the heat capacity of nanofluid. In terms of temperature field, the heat fluxq″ is defined as

(17)

whereKNFis the nanofluid thermal conductivity, which is defined as

(18)

The pressure is approximately uniform andT=T(x,y) in the present problem, so Eq.(11) becomes

(19)

The corresponding boundary conditions are

(20)

u→0,T→T∞asy→∞

(21)

By introducing the following non-dimensional variables

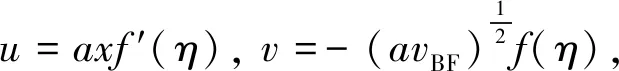
(22)

Using the Rosseland approximation[27], in Eq.(19), and incorporating above non-dimensional variables into Eq.(14) and Eq.(19), we obtain the following equations

(23)

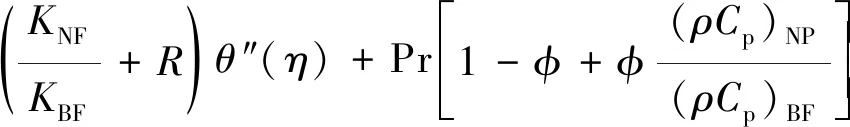
θ′(η)f(η)=0

(24)

The boundary conditions become

f(η)=0,f′(η)=1,θ′(η)=-γ[1+θ(η)],η=0

(25)

f′(η)→0,θ(η)→0,η→∞

(26)

where

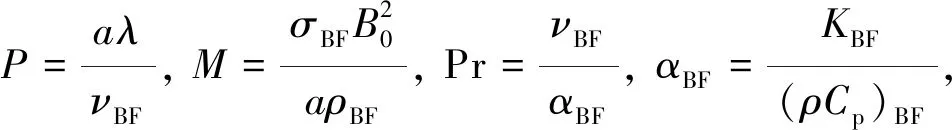
3 Exact solutions

3.1 Momentum equation

Follow the HAMAD[28], the exact solution of Eq.(23), subject to the boundary conditions (25) and (26), is obtained as

(27)

where

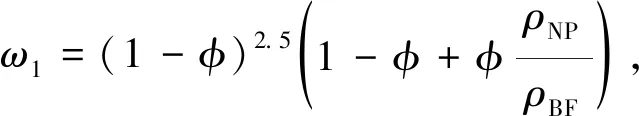
3.2 Heat equation

Substituting Eq.(17) into Eq.(24), we get

(28)

where

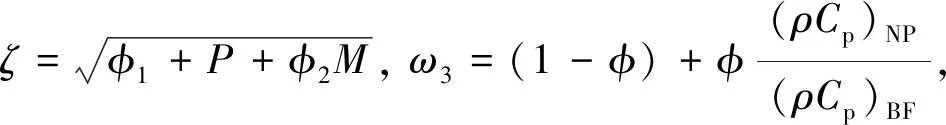
By usingτ=exp(-ζη), the above equations transform to

(29)

with transformed boundary conditions

(30)

The analytic solution of Eq.(29) in term of independent variableτis

θ(τ)=D1+D2

(31)

whereD1andD2are constants and

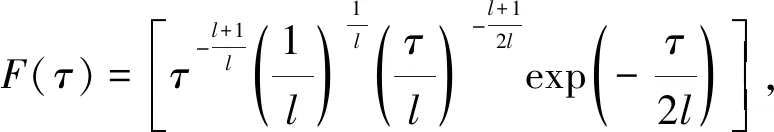
where

The analytical solution can be easily obtained by substitutingD1andD2into Eq.(31). Final solution of temperature in form ofηcan be obtained by replacingτ=exp(-ζη) in Eq.(31).

4 Graphical results and discussion

The effects of different parameters such as magnetic parameterM, porosity parameterP, Newtonian heating parameterγ, radiation parameterR, Cu nanoparticles volume fraction and Fe2O3nanoparticles volume fraction on the velocity and temperature fields are sketched graphically in Fig.1 to Fig.7. The thermo-physical properties of Cu and Fe3O4nanoparticles and water have been given in table 1.

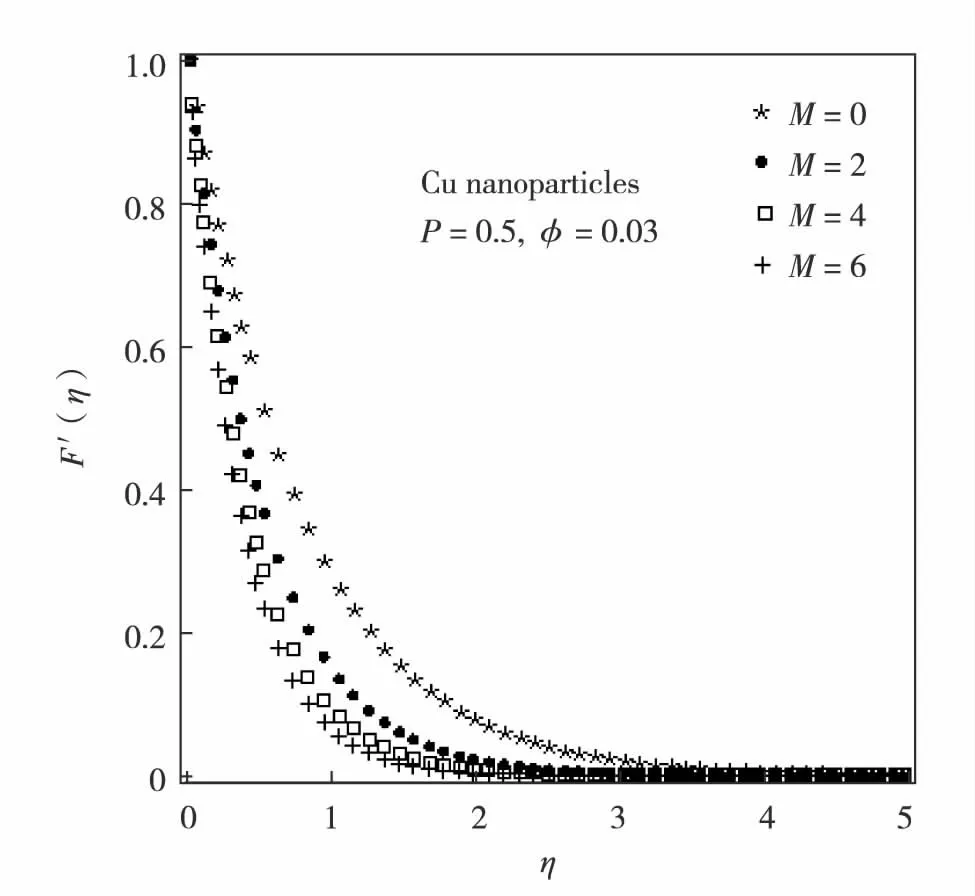
Fig.1 Velocity field of Cu-water based nanofluid for different values of M图1 Cu-水纳米流体的速度场 相对M的变化值

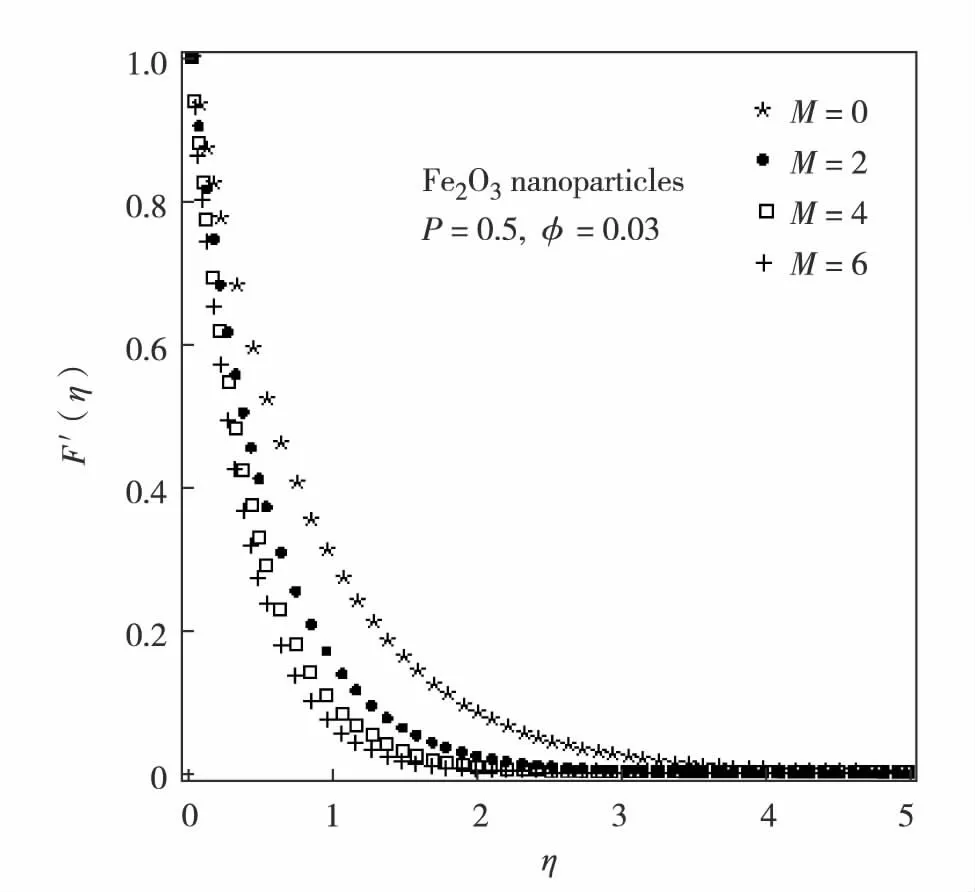
Fig.2 Velocity field of Fe2O3-water based nanofluid for different values of M图2 Fe2O3 -水纳米流体的速度场 相对M的变化值

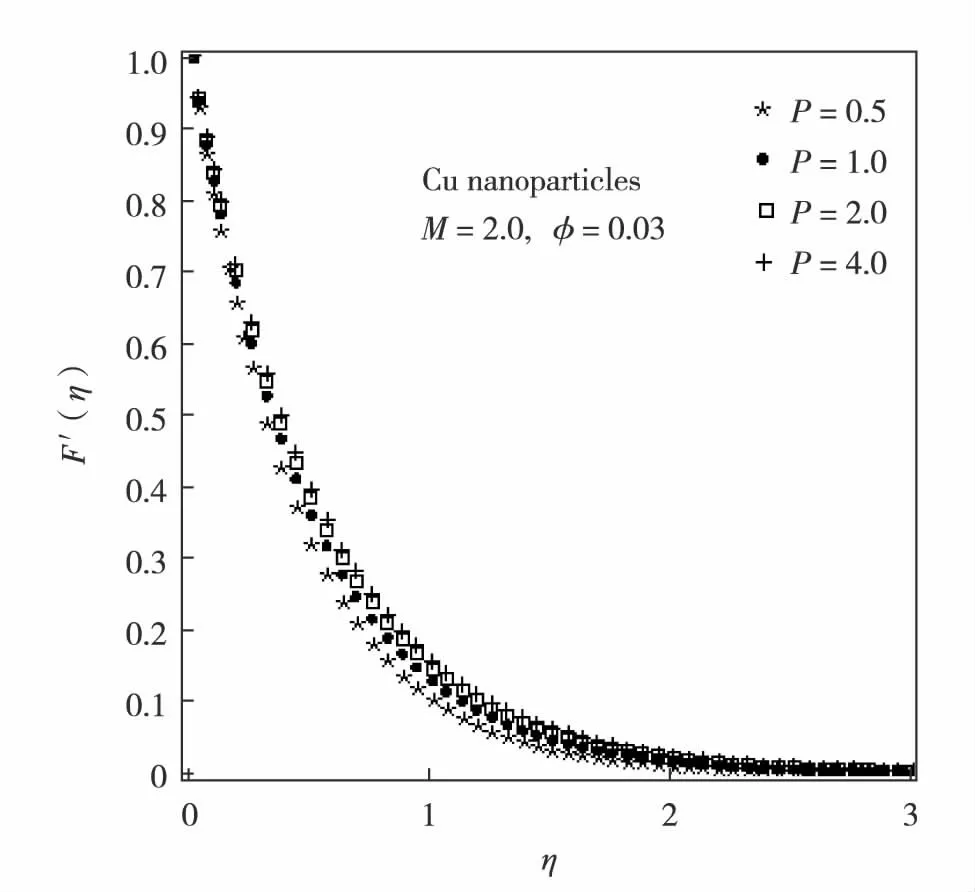
Fig.3 Velocity field of Cu-water based nanofluid for different values of P图3 Cu-水纳米流体的速度场 相对P的变化值

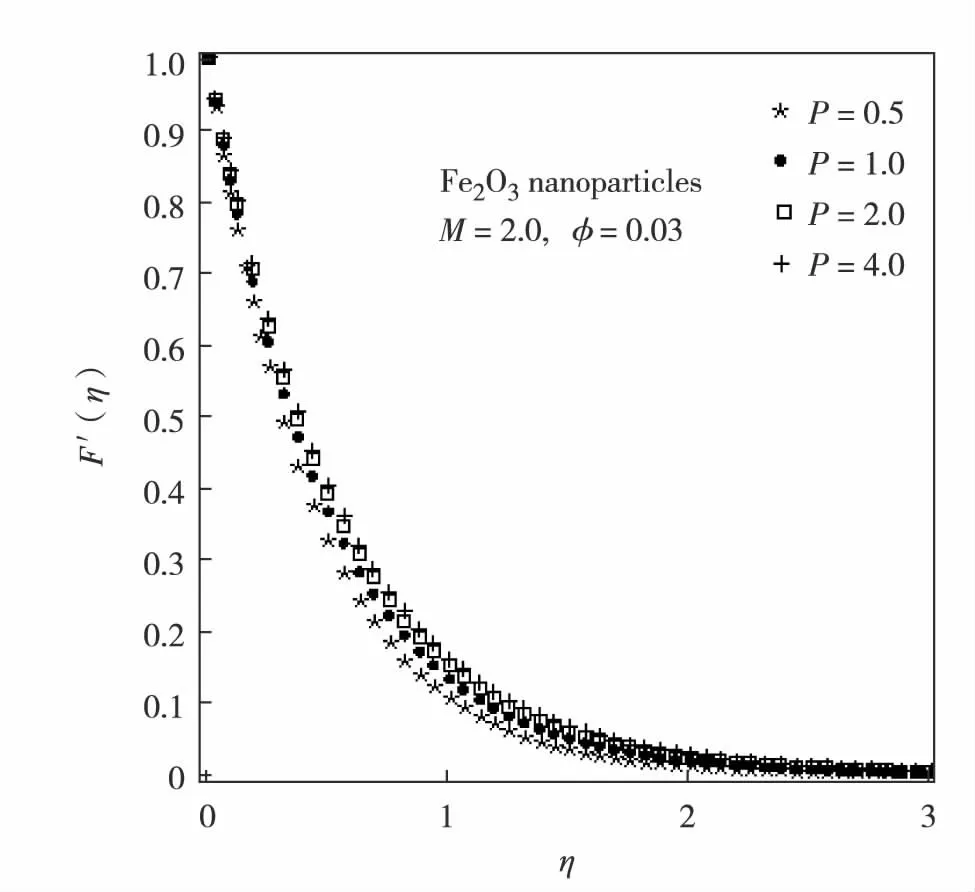
Fig.4 Velocity field of Fe2O3-water based nanofluid for different values of P图4 Fe2O3 -水纳米流体的速度场 相对P的变化值

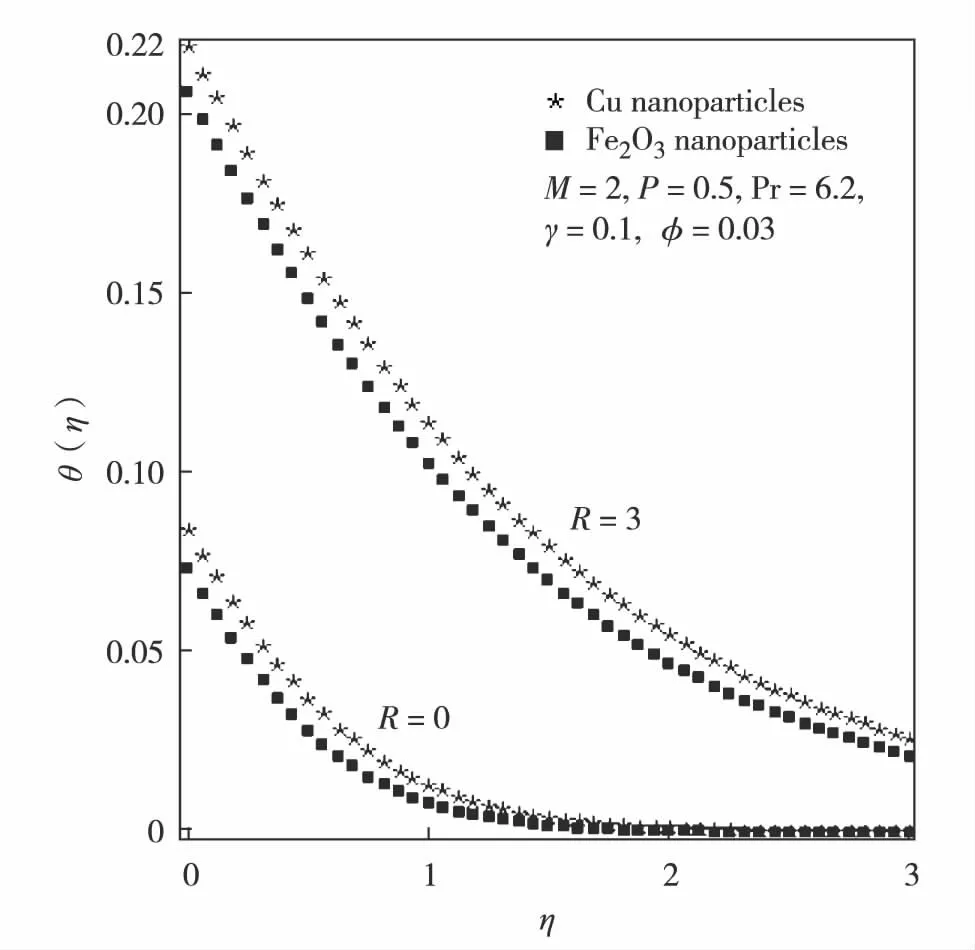
Fig.5 Temperature of Cu and Fe2O3 based nanofluids for different values of R图5 对应Cu 和 Fe2O3 的纳米流体的 温度分别相对R的变化值

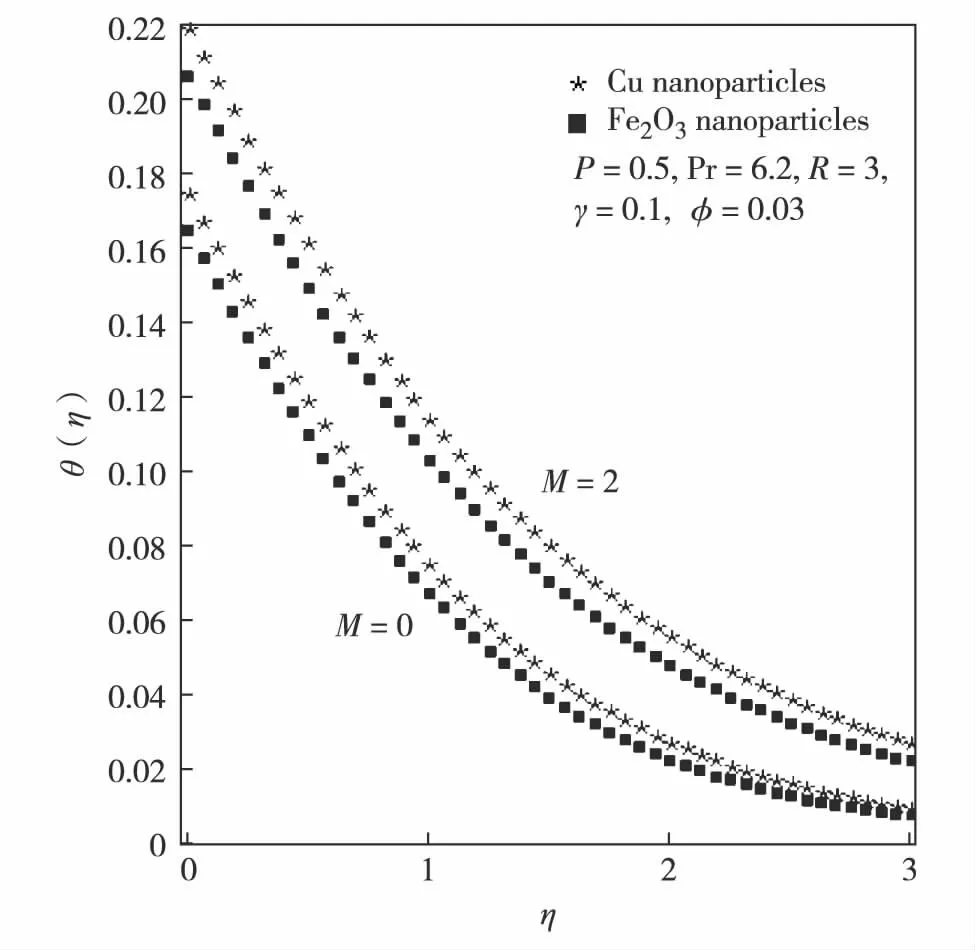
Fig.6 Temperature of Cu and Fe2O3 based nanofluids for different values of M图6 对应Cu 和 Fe2O3 的纳米流体的 温度分别相对M的变化值

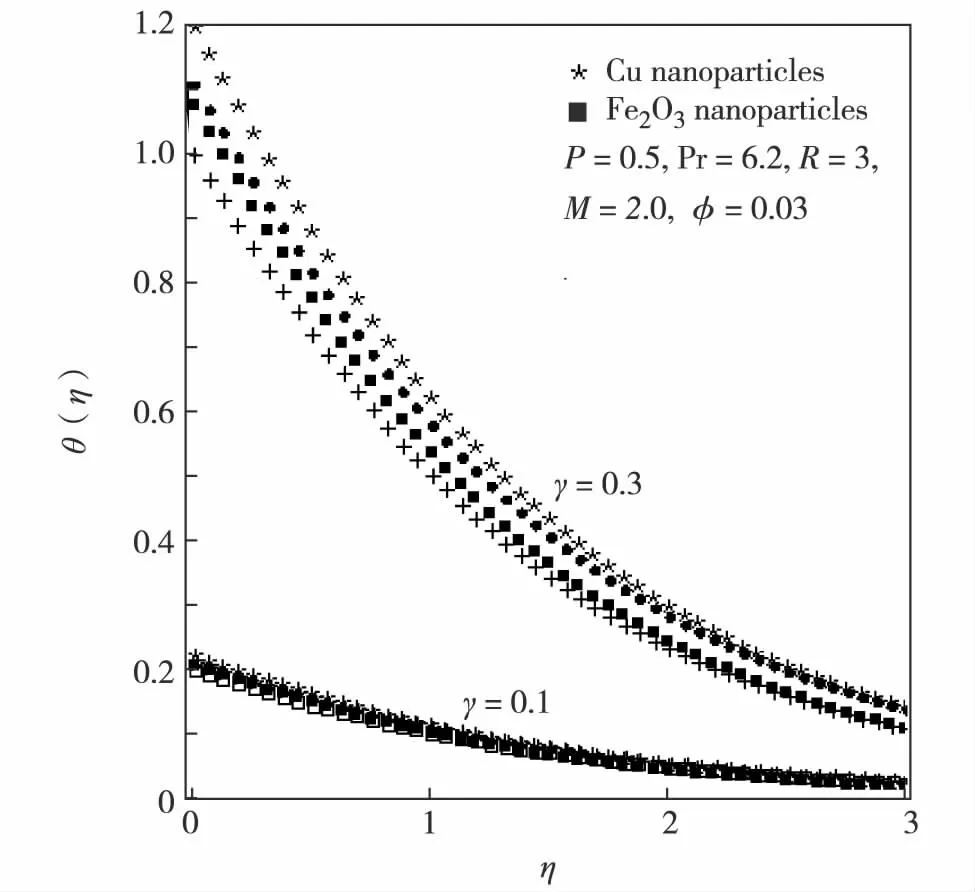
Fig.7 Temperature of Cu and Fe2O3 based nanofluids for different values of γ图7 对应Cu 和 Fe2O3 的纳米流体的 温度分别相对于γ的变化值

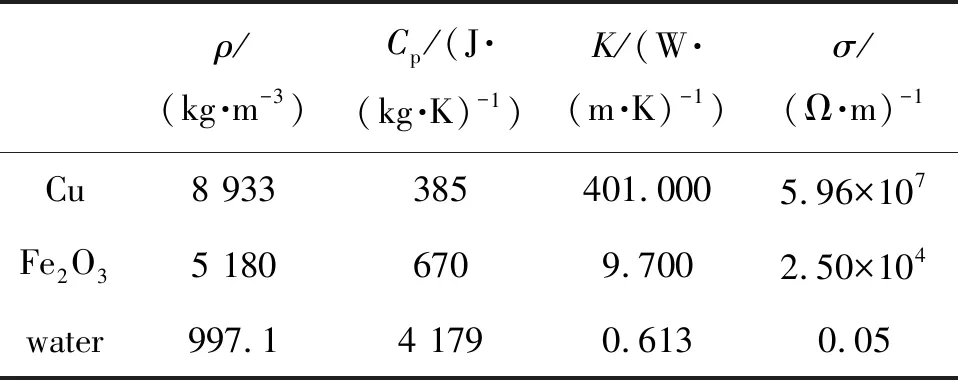
Table 1 Thermo-physical properties of Cu, Fe3O4 and water表1 Cu, Fe3O4和水的热物理性质

The velocity profiles are plotted in Fig.1 and Fig.2 for various values of magnetic parameterMin the presence of magnetic field (M≠0) as well as in case of purely hydrodynamic flow (M=0). It is found that in the absence of magnetic field, the velocity has its maximum value and it decreases whenMincreases for both Cu-water and Fe2O3-water based nanofluid. This behaviour is in accordance with the physical observation that the application of transverse magnetic field always results in a resistive type force also called Lorentz force. This type of resistive force tends to resist the fluid flow and thus reducing the fluid motion significantly. In Fig.3 to Fig.4, the impacts of porosity parameterPon Cu-water and Fe2O3-water based nanofluid velocities are shown at the fixed value of magnetic parameterM=2. It is known that permeability of a medium is related to the porosity. The permeability shows the ability of a porous material to allow fluids to pass through it. In consequence of porosity enhancement, permeability is amplified which leads to augmentation of fluid flow in supposed porous medium. Therefore, velocity field is increased due to porosity enhancement.

Fig.5 shows the temperature field comparison between Cu-water and Fe2O3-water based nanofluids in the absence of thermal radiation (R=0) as well in the presence of thermal radiation (R≠0) under fixed magnetic field. It is found that the nanofluid containing Cu nanoparticles has higher heat transfer rate than Fe2O3-water based nanofluid. Since the thermal conductivity of Cu has the highest values compared to Fe2O3, its dispersion into water raises the thermal conductivity of water based nanofluid and thus the rate of heat transfer increases. Furthermore, with regards to the constant magnetic field and nanoparticles volume fraction, the increase of radiation parameterRleads to the increase of heat transfer.The change in temperature field with the variation in magnetic interaction parameterMis elucidated in Fig.6. The results of Cu-water and Fe2O3-water based nanofluids in the presence of magnetic field (M≠0) are compared with the corresponding results in case of purely hydrodynamic flow (M=0). A growth in temperature field is anticipated for growing magnetic field strength. The increasing magnetic field strength reduces fluid velocity due to that less hot fluid is carried away from the sheet. This in turn decreases wall temperature gradient, which implies a growth in thermal boundary layer thickness. From Fig.7, it is found that as the Newtonian heating parameterγincreases, so does the thickness of the thermal boundary layer and as a result, the sheet temperature increases.

Conclusions

Nanofluid flow and heat transfer with magnetic (Fe2O3) and non-magnetic (Cu) nanoparticles are investigated by using the single-phase model. The magnetic field influences have been taken into account. The nanofluid shows great potential in enhancing the heat transfer process. One reason is that the suspended nanoparticles remarkably increase the heat transfer performance of the nanofluid. Furthermore, the results show that the heat transfer performance of Cu-water and Fe2O3-water nanofluids in the presence of thermal radiation is better than those in the absence of thermal radiation.

Nomenclature

aPositive constant

bBody force

B0Strength of magnetic field

Cp,NFNanofluid heat capacity

hsHeat transfer coefficient

KBFThermal conductivity of base fluid

KNPNanoparticle thermalconductivity

KNFNanofluid thermal conductivity

MMagnetic parameter

PPorosity parameter

Pr Prandtl number

qrRadiative heat flux

RRadiation parameter

TTemperature of the fluid

T∞Ambient temperature

λPermeability

γNewtonian heating parameter

δMean absorption coefficient

φNanoparticle volume fraction

αBFBase fluid thermal diffusivity

μBFBase fluid dynamic viscosity

μNFNanofluid dynamic viscosity

ρBFDensity of base fluid

ρNPNanoparticle density

ρNFNanofluid density

σ*Stefan-Boltzmann constant

σBFElectric conductivity of base fluid

σNPNanoparticle electric conductivity

σNFNanofluid electric conductivity

θDimensionless temperature