精心变题以导思——初中数学变题训练的思考

江苏省扬州市高邮市秦邮初级中学 赵 娟

朱熹曾说过：为学乃能变化气质耳。教育的作用在于“变化气质”，但变化气质的前提是转变思想。思想是影响气质的重要因素，而思想是受思维所影响的。由此，教育的目的就是要培养学生灵活的思维。然而，在教育现实中思维训练往往被一些教育者忽略，尤其是在初中数学解题教学中，很多老师认为只要教给学生解题方法，好像他们就无往而不利。事实上，方法只是一种辅助学习的工具，重要的是学生思维能力，这才是帮助他们实现终身学习的根本。数学学科被称之为“思维的体操”，可见它在提高学生思维能力方面有着比其他学科更明显的优势。笔者从实践中发现，合理运用变题训练对激活中学生数学思维有着显著效果，以下是结合教学实践对如何“精心变题以导思”进行的详细阐述。

变题训练之——“旧题显新意”

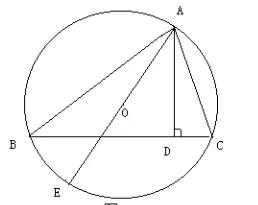
图1

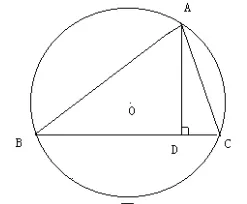
图2

数学知识之间有着密切的联系，彼此之间互相渗透，但教材毕竟有限，教材中选择的一些习题和例题一般知识面都相对较窄，对于学生知识的综合运用能力培养略有欠缺，也容易让学生形成思维定势。这时如果适当给旧题注入一些“新意”，进行一下知识体系的置换，学生思维就会变得活跃，问题分析能力也会大大提高。如在学习“几何”时，有题如下：“如图1所示，三角形ABC的高是AD，外接圆直径是AE。求证：AB·AC=AE·AD。”这道题主要考量学生如何运用相似形、圆等性质进行等积式问题的证明，但如果稍加变化，就会让该题变成一道集几何、代数为一体的综合知识运用题型。变题后成为：“如图2所示，已知锐角三角形ABC的外接圆圆O的半径是10厘米，AB的长度是8厘米，AC的长度是5厘米，求边BC上的高AD的长度是多少。”经过变化之后的“新题”，圆的直径并没有直接给出，但因为通过原题解答之后，学生能够很快将隐藏于题中的条件找到并将直径计算出来，所以之前的“证明题”就变身为“几何计算题”，这是在原题基础上增加了一定的广度和深度，这对学生数学应用能力以及问题分析能力均有提高，在应用与分析中，学生思维就会得到有效锻炼。

变题训练之——“举一还反三”

在初中数学解题练习中，学生非常容易形成思维定势，当他们熟悉了某一种题型的某种解法时，就会被局限于这种题型之中，只要题目稍加变化就会出现思维障碍，容易出错。而在数学教学中进行变题训练的目的就是帮助学生打破这种定势思维，通过对题目中一些条件、图形、结论等内容的变化，引导他们学会如何对类型相同或相近的一系列题型进行思考，在题目性质不变的前提下将问题的形式与内容进行变化，让他们在举一反三中找到知识之间存在的内在联系，从而把握住数学本质性规律，让发散性思维、逻辑性思维等均获得发展。

例如条件改变的变题训练，原题为：“如果依次将三角形三条线段的中点进行连接，我们会得到一个怎样的图形？”通过条件改变后变成：

①如果依次将等边三角形的三条线段的中点进行连接，我们会得到一个怎样的图形？

②如果依次将等腰三角形的三条线段的中点进行连接，我们会得到一个怎样的图形？

这种变题训练主要是对学生几何图形处理以及空间思维能力进行的锻炼，而通过对条件进行的巧妙变化，三角形由原题中的一般三角形变成了等边或者是等腰三角形，看似好像条件只是进行了简单附加变化，但解题结果却发生了很大变化，学生通过这样的变题训练会对三角形结构有了更深入的理解和认知。

变题训练之——“一题有多解”

一道题是不是只有一种解法？显然并不是，一道题可以有很多解法，而每一个解法代表的是不同的思维过程，因此通过“一题多解”的变题设计，让学生学会从多种角度对问题中包含的各种数量关系进行思考分析，通过寻找不同解法去建立起知识之间的密切联系，是对学生思维灵活性最好的训练。如：“一条线段是另一条线段两倍”的证明方法有几种？最常规的方法学生都知道，就是先作出短线段的“二倍线段”，再证明长线段与“二倍线段”相等即可。那是不是还有其他方法？很显然，从第一种方法中，学生自然也会想到“反之亦然”的道理：将长线段取其一半，证明短线段与其相等也可以。这基本属于同一思维过程的方法，那还有其他的吗？在老师的鼓励引导下，有的学生想到了假设长线段为直角三角形某一斜边，那么可以通过取中线的方法进行证明。这很显然是一个思维的突破，而在这个同学的启示下，有的学生想到了如果具备了四个以上“中点条件”，那么可以通过“三角形中位线定理”进行证明。这样一来，简单的问题呈现出多样化的解决方法，这既可以使数学思想方法得到巩固，还可以让学生触类旁通，抓住数学的本质。

总之初中数学教学中的变题训练，就是将一个个看起来好像没有联系的孤立问题，通过向多种角度进行拓展，最终形成有规律的方法体系。学生可以在问题探究中找到解决系列问题的方法，学会如何独立地对数学科学领域进行探索和研究，从中体验到数学知识的奇异美与和谐美，实现数学思维、数学能力的提高。