找到事物的另一面，实现巧妙的转化——以四边形分类新秩序为例

江苏省常州武进区卢家巷实验学校 岳丽芬

读过一个经典的佛理故事，名字叫《佛经对了，佛就笑了》，内容是一位禅师，惩罚寺院里一名不守清规的弟子，罚他面壁思过。墙壁上挂着一幅弥勒佛画像，禅师给受罚弟子出了一道难题，也算是一次将功补过的机会，禅师随手将画像撕成很多碎片，让弟子在一炷香的时间内拼完，按时完成任务就可以提前恢复自由，否则只能乖乖挨罚。

令禅师万万没想到的是，不到一盏茶的工夫，受罚的弟子就拼完了画像。禅师感到震惊和纳闷，因为他是第一个破解难题，成功逃脱面壁惩罚的弟子，禅师急忙问其究竟。

弟子回答：“佛像背面是一行行用欧体正楷抄写工整的佛经，是《法华经》中的一段，我背得滚瓜烂熟，只要把佛经还原了，弥勒佛画像也就拼好了。”故事结尾有一句发人深省的话：“佛经对了，佛就笑了。”

单从考虑问题的智慧来说，这个弟子的做法的确出人意料，如果老老实实按照要求去做很难完成任务，可是这个弟子却懂得变通，将原问题转换成另一个问题，降低了难度，顺利解决问题，也就是将一个复杂的问题（佛像的拼接）转换成另一个简单的问题（佛经的拼贴）。

这个哲理故事告诉我们转化思维多么神奇和重要，在小学数学中，求图形的面积时，转化思维可以大显神通。

一、接入转化思维，重新分类定秩序

本文着重要讲的是四边形的面积及其分类，先说分类。在教材中，根据对边平行的情况，可以将其分为三类：第一种是没有对边平行，第二种是只有—组对边平行，第三种是两组对边都平行。分类情况如下图：

在这个分类中，四边形被分为三大类：只有一组对边平行的四边形（梯形）、两组对边都平行的四边形（平行四边形），这是两大类，空白处为一般四边形，是小类，极易被忽略。在这种分类法里，极易让人产生误会：四边形除了梯形就是平行四边形，二者合并起来构成全部四边形，其实这种分法欠妥。

在这种分类里，平行四边形和梯形是并列关系，平行四边形里又包含长方形，长方形里又包含正方形。

如果我们换种分法，另行设立分类标准——“有无对边平行”，平行四边形则被分为两大类：1.没有对边平行；2.有对边平行。在第2类里面又分很多小类，小类的细化就是不断增加附属条件，丰富内涵，缩小外延。如仅仅说明一组对边平行，则为梯形；若梯形中的另一组对边也平行，则为平行四边形；若梯形的另一组对边平行且有一个内角为直角，则为长方形；若梯形的另一组对边平行且含有一个直角内角且邻边相等，则为正方形。

在这种分法下，平行四边形属于梯形的一部分，是一种比较特殊的梯形，换言之，二者不再是并列关系，而是包含关系。分类图如下：

二、确立新的标准，重新表述缩外延

各种分类方法都有其合理性，那么这种分类的优势在哪？

对照下列语句：

对于一个四边形，假若有一组对边平行，则为梯形；

对于一个四边形，假若有一组对边平行且相等，则为平行四边形；

对于一个四边形，假若有一组对边平行且相等，还有一内角为90度，则为长方形；

对于一个四边形，假若有一组对边平行且相等，而且还有一内角是90度，此外发现邻边也相等，则为正方形。

可以发现，随着对“梯形”概念内涵的拓宽，其外延在不断缩小。这种一般到特殊的分类符合演绎推理的逻辑思维。

三、越过中间环节，一步到位求面积

在小学数学中，要求学生掌握各种四边形面积的计算。

教材中对各种图形的面积公式推导，包括三角形在内，都是从长方形开始的。首先规定各面积单位的原始定义，用数方格的方法，归纳出长方形的面积公式：长方形的面积=长×宽。

长方形的面积公式出炉后，继续转化，以长方形面积公式为基础，用割补法将平行四边形变换为长方形，推出平行四边形面积=底×高。梯形和三角形也是这样，都是转化为平行四边形后，再来推导。

在四边形的新分类法中，可以先由长方形推出梯形面积，因为其他四边形和三角形都可以视为特殊的梯形，所以在梯形为转化标准的情况下，梯形面积公式可以演变为其他图形面积公式。

那么梯形的面积公式从何而来呢？可以按照教材安排，先将梯形转化为平行四边形，再将平行四边形转化为长方形，导出其面积公式，也可以一步到位，将梯形直转成长方形，然后推导面积公式。如图1：

图1

已知梯形ABCD的上底长为a，下底长为b，高为h。求面积。如图，将梯形分成①、②、③三大区块，各区域面积为：

观察可知：DG=HC。

所以S1+S2+S3

=DG×h÷2+a×h+HC×h÷2

=h×(DG+HC)÷2+ah

=h×(b-a)÷2+ah

=bh÷2-ah÷2+ah

=bh÷2+ah÷2

=(a+b)h÷2

针对图2，图3这两个梯形，可以如法炮制。

图2

图3

以梯形面积公式为母本，根据平行四边形的上下底相等的特殊性，推导其面积为(a+a)×h÷2=ah。

对于三角形的面积公式，也可以通过梯形面积转化而来。如图4，梯形ABCD中，上底长为a，下底长为b，高为h。

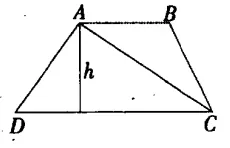
图4

设B点为动点，沿上底向左移动，行至A点后停止运动，此时梯形上底缩短至一个点，长度变为0。梯形同时变形为三角形，代入公式有：S三角形=（0+b）×h÷2=bh÷2。

不同的思路，会产生不同的分类标准。所谓转化思想，其实就是转换一种思路，最终达到同样的目标。本文仅从四边形分类与面积重新推导来阐述，纰漏之处还请专家同行批评指正。