基于线性二次型的电动汽车最优驱动控制系统的设计与仿真分析

刘旭杰,徐惠民,陈 丰

安徽科技学院机械工程学院，安徽凤阳,233100

我国正在推动燃油车禁售规划[1]，目前国内外的新能源汽车大多数是采取油电双混的动力方案。笔者查阅有关资料，以比亚迪和特斯拉为代表的国内外新能源汽车大都采用双电机驱动系统，主副驱动电机都是永磁同步直流电机，当汽车处于高速行驶状态下使用主电机驱动，当汽车处于低速状态下需要较大的输出转矩时,副电机工作或者主副电机一起工作。虽然这种驱动方式总体调速特性好，但却增加了汽车的重量，同时也降低了其续航能力，相较于传统燃油汽车还是存在较大缺陷，所以目前市面上较好的所谓的新能源汽车大都采用的是油电双混的动力系统。

众所周知，电动汽车的三个主要研究内容是电池、电机、电控系统。本文将从电机与电控系统两个方向着手，为电动汽车提供一种新的驱动方案。电动汽车为了增加其续航能力，需要控制电路可以实现“再生制动”，将车辆制动时损失的动能以电势的形式回收到电源中，因此传统的PID控制很难实现电动汽车工作时的控制要求。将IGBT模块加入PID控制电路中，既能保留传统PID控制的优点,又能降低控制系统驱动功耗提高续航能力，而且可以提高开关响应速度，实现电动汽车的“再生制动”。线性二次型(Liner Quadratic，以下简称LQ)最优控制发展至今已经趋于成熟，相较于模糊遗传控制算法、参数自适应控制算法、卡尔曼滤波器、变结构控制算法、神经网络算法、鲁棒控制算法，LQ最优控制算法虽不能达到他们的精度，但是用在电动汽车上已是足够。LQ最优控制方法虽然在加权矩阵参数的选择上工作量稍大，但其实现过程简单、成本低，同时又能使整个系统在控制过程中性能最优化，且控制精度足够，是电动汽车控制系统优化方法中的较佳选择。

1 电动汽车驱动电机设计

直流永磁同步电机作为电动汽车的驱动电机，具有无电刷、运行可靠、调速性能好、控制效率高、体积小等优点，是当前大多数电动汽车制造业首选的驱动电机，目前在日本电动汽车行业中率先得到了普遍的应用。但一台直流永磁同步电机无法同时满足电动汽车低速和高速状态下的调速要求，所以目前像比亚迪和特斯拉这样的国内外电动汽车生产商均是采用双电机动力系统，这种驱动系统虽然满足了电动汽车的工作要求，但增大了耗电量和车体重量，降低了车辆的续航能力。所以，为了兼顾电动汽车高低速的调速要求、车体轻量化、电源续航能力，本文设计了一种带有增磁绕组的直流永磁同步电机，当汽车在低速时该电机能提供足够的输出转矩，当高速时关闭增磁绕组以节省电量消耗，增加续航能力。同时该电机兼具直流永磁同步电机的体积小等特性，将是未来电动汽车驱动系统的首选。通过实际测量该电机的转矩转速特性如图1实线所示，同时图中虚线部分还给出了直流永磁同步电机的转矩转速特性。

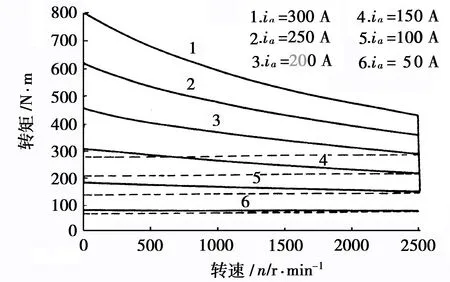
图1 加装增磁回路电机的转矩—转速特性

2 电动汽车驱动控制系统的设计

该电机的控制系统见图2。在该系统中，B表示汽车的电池组，其输出电压为384 V；被控电机由电枢绕组、增磁绕组L1以及永磁励磁部分L2组成；电路中，S1、S2是电流传感器检测模块，S1用于功率模块过流保护，S2用于测量驱动电机电枢电流ia[2]；加速时，以单片机为核心的控制单元接收加速度信号和来自S2的电枢电流ia，将二者进行比较，然后通过调整IGBT1的高频脉冲宽度改变电枢电压ua的大小,进而使电枢电流和给定加速度信号处于同一水平，这一过程中IGBT2始终处于关断状态。制动时，没有加速度信号输入，IGBT1处于关断状态，控制单元接收制动信号，然后由控制单元向IGBT2输送相应的脉冲调宽信号，此时该模块导通，电动机M制动时产生的反电势通过该模块被回收，从而实现“再生制动”[3]。

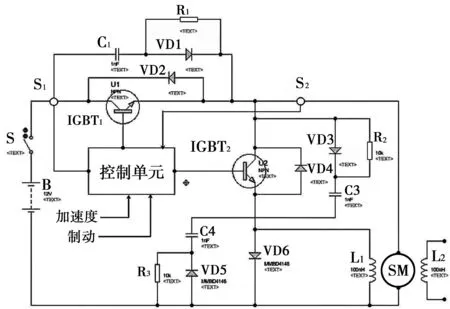
图2 电动汽车驱动电动机控制系统原理图

本文为了简化相关的分析过程，进行如下几点假设：

(1)忽略电机内部的铁芯饱和，不计内部产生的涡流损耗和磁损；

(2)忽略电枢感应对电机运行的影响，且永磁体作为复励电机的他励部分所提供的磁场是稳定不变的；

(3)忽略齿槽效应认为电枢表面连续均匀地分布着电枢导体[4]；

(4)假设所有模块工作状态、续流二极管开关特性均是在理想状态下。

以上四点假设，保证了普通并励电机的微分方程、传递函数成立，据此建立永磁加增磁的复励电机的数学模型[5]。

2.1 普通并励电机数学模型

根据并励电机的电压—电流特性、电枢电流—转矩特性、转矩—加速度特性及电动机转动时产生的反电动势之间的关系，得到如下关系式[6]:

(1)

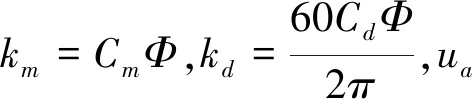
令1/Ra=ka、La/Ra=Ta，代入上式并且经过拉普拉斯变换后得到无增磁回路的牵引电机的系统传递函数方框图如图3所示[7]。

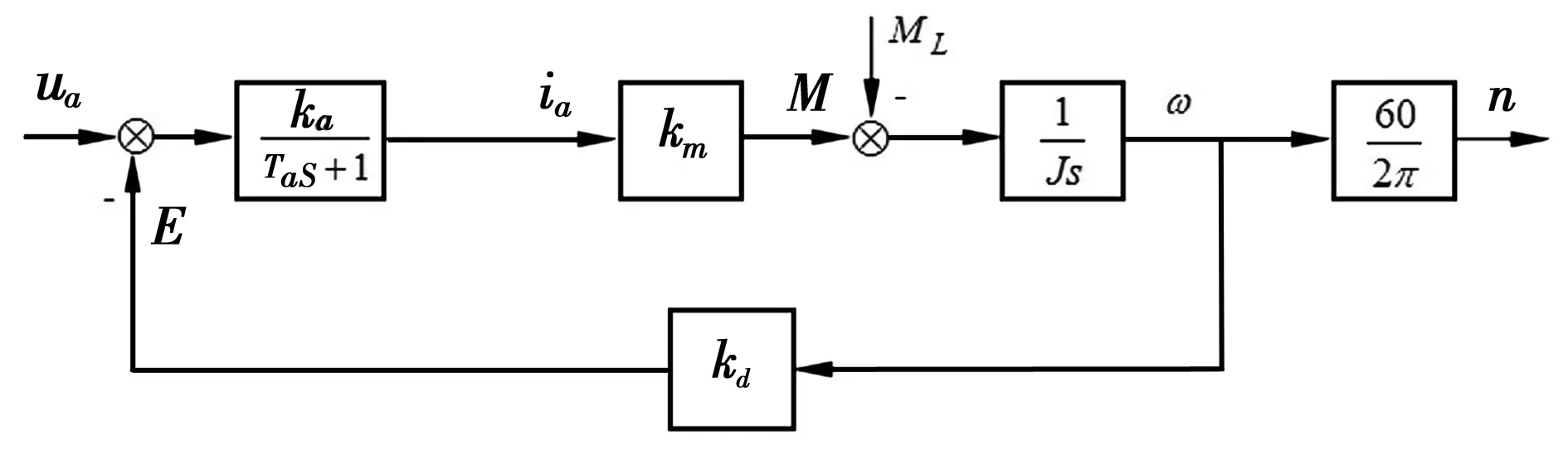
图3 无增磁回路的牵引电机的系统传递函数方框图

2.2 加装增磁回路的电机数学模型

该电机的输出转矩M与电枢电流ia以及转速n之间的函数关系如下:

M=f(ia,n)

(2)

在其工作点使用微元法线性化后得到上式的增量方程如下:

(3)

令ke=(2π/60)kd，根据式(3)以及图3可以得到永磁加增磁回路的复励电机的传递函数方框图，见图4(图中省略了Δ)。

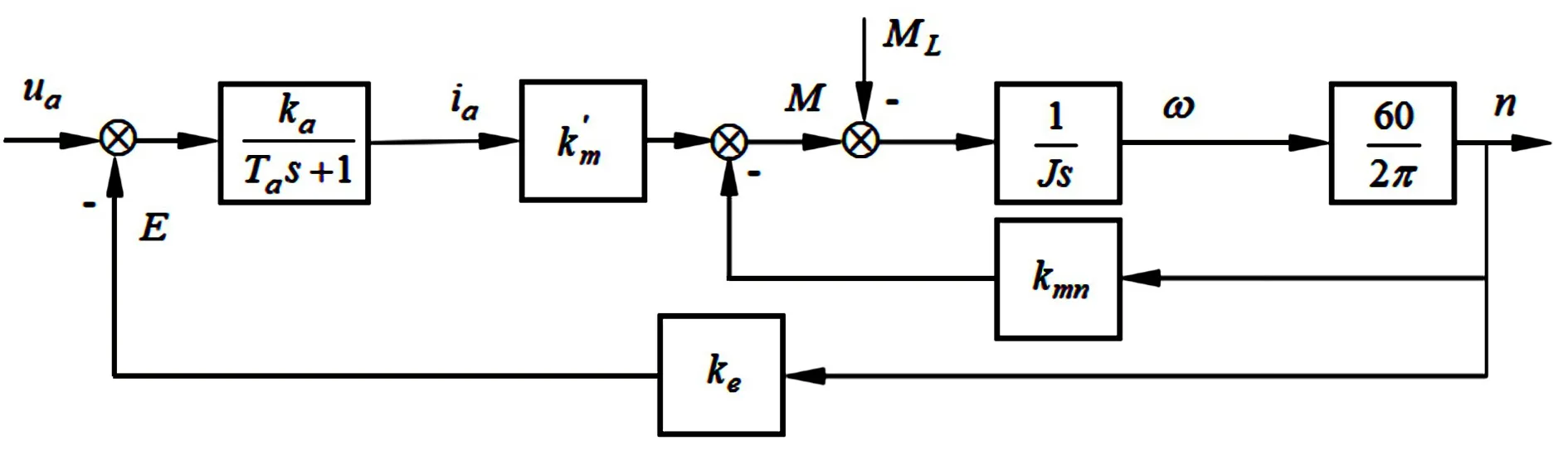
图4 永磁加增磁回路的复励直流电机传递函数方框图

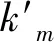
2.3 电机加速度控制系统数学模型

由图2控制电路可知，控制单元比较加速度输入信号与电枢电流ia强度后，调整IGBT1模块脉冲调频宽度和电枢电压ua，最终改变电枢电流强度，使其实际加速度与给定信号一致[8]。根据该控制过程给出加速度控制系统模型如图5。

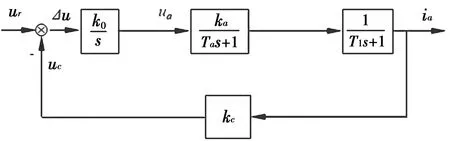
图5 加速度控制系统传递函数方框图

图中：ur为经过控制单元转换过的加速度信号；ia为电流传感器采集到的电枢电流；kc为该驱动控制电路中电枢电流与电压的比例系数；uc为ia经kc积分后对应的实际加速度信号；T1为IGBT1中的RC和电流传感器中的RC电路形成的惯性环节。

取k0=251.12 s-1，查电工手册驱动电机相关参数得：La=5 mH，Ra=0.038 35 Ω,所以有ka=1/Ra=1/0.038 35≈26.08；Ta=La/Ra=5×10-3/0.038 35≈0.13 s；RC电路惯性时间常数估算值为T1=0.02 s，实验中测得，当ia=300A时电流传感器的输出电压为5 V，因此kc=5/300≈0.02 V/A[5]。

图5的闭环传递函数为:

(4)

将所有参数代入上式得:

(5)

根据式(5)可以将图5所示的控制器传递函数模型简化为图6。

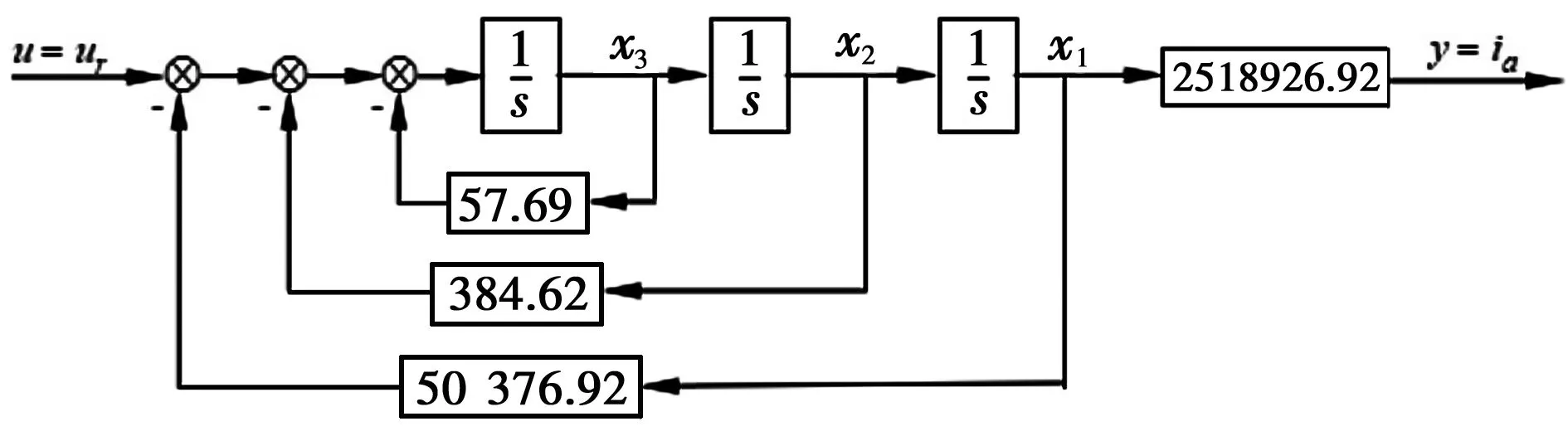
图6 加速度控制器简化模型

根据简化后的控制器模型写出其状态方程如下：

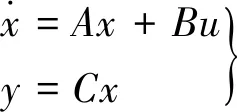
(6)

其中

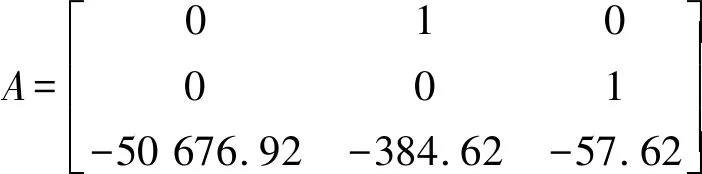
3 电动汽车加速度控制系统的优化设计

3.1 驱动控制系统稳定性分析

根据矩阵A使用MATLAB软件求其特征值，得到该系统的特征根如下：

(7)

因为特征根中只有一个实部为负数，所以该系统是不稳定的[9]。

3.2 LQ指标最优控制器设计

根据该系统特点确定其LQ性能指标为[8]：

(8)

(1)当取Q(t)和R(t)的参数值如下：

使用MATLAB求得其状态反馈系数K与对应黎卡提方程解P如下：

K=[k1k2k3]=[0 815.498 8 12.750 9]

(9)

此时对应的闭环系统特征根为：

(10)

(2)扩大加权矩阵Q，并且保持加权矩阵R大小不变，即：

经MATLAB求得其状态反馈系数K与对应里卡提方程解P如下：

K=[k1k2k3]=[0 2 440.6 77.3] (11)

(12)

此时该系统对应的特征根为：

(13)

(3)再次扩大加权矩阵Q，并且保持加权矩阵R大小不变，即：

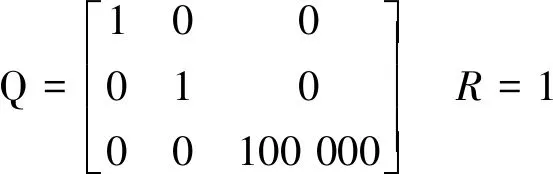
经MATLAB求得其状态反馈系数K与对应里卡提方程解P如下：

K=[k1k2k3]=[0 4 945.5 278.8]

(14)

(15)

此时该系统对应的特征根为：

(16)

4 系统特性仿真

加入状态反馈环节后，其闭环传递函数如下：

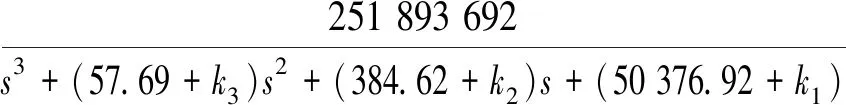
(17)

加入状态反馈环节后，其系统传递函数方框图如图7。

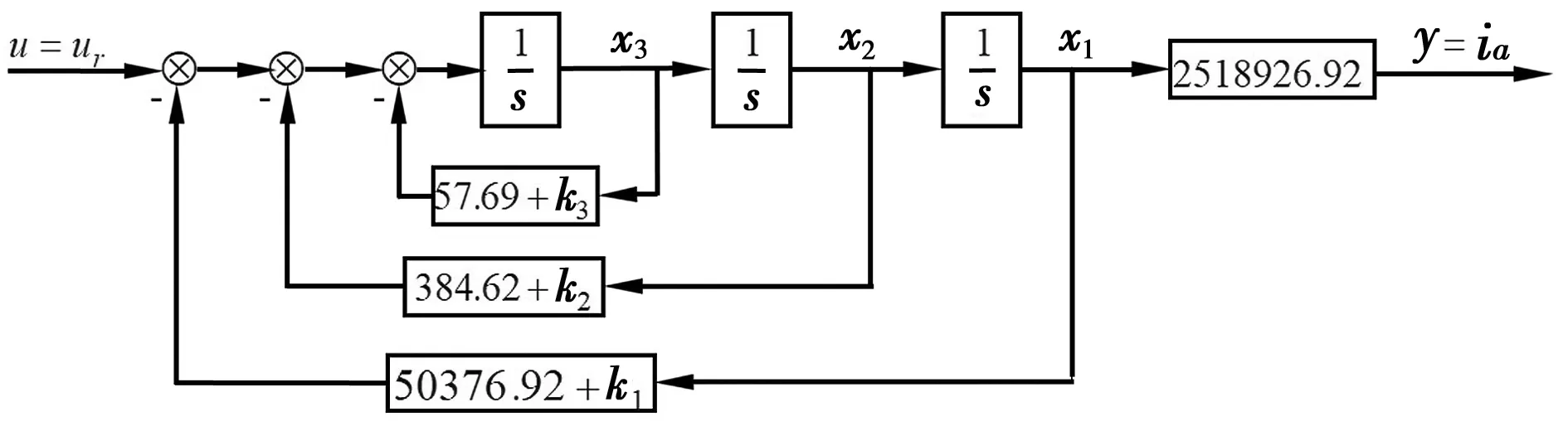
图7 带有状态反馈的系统传递函数方框图

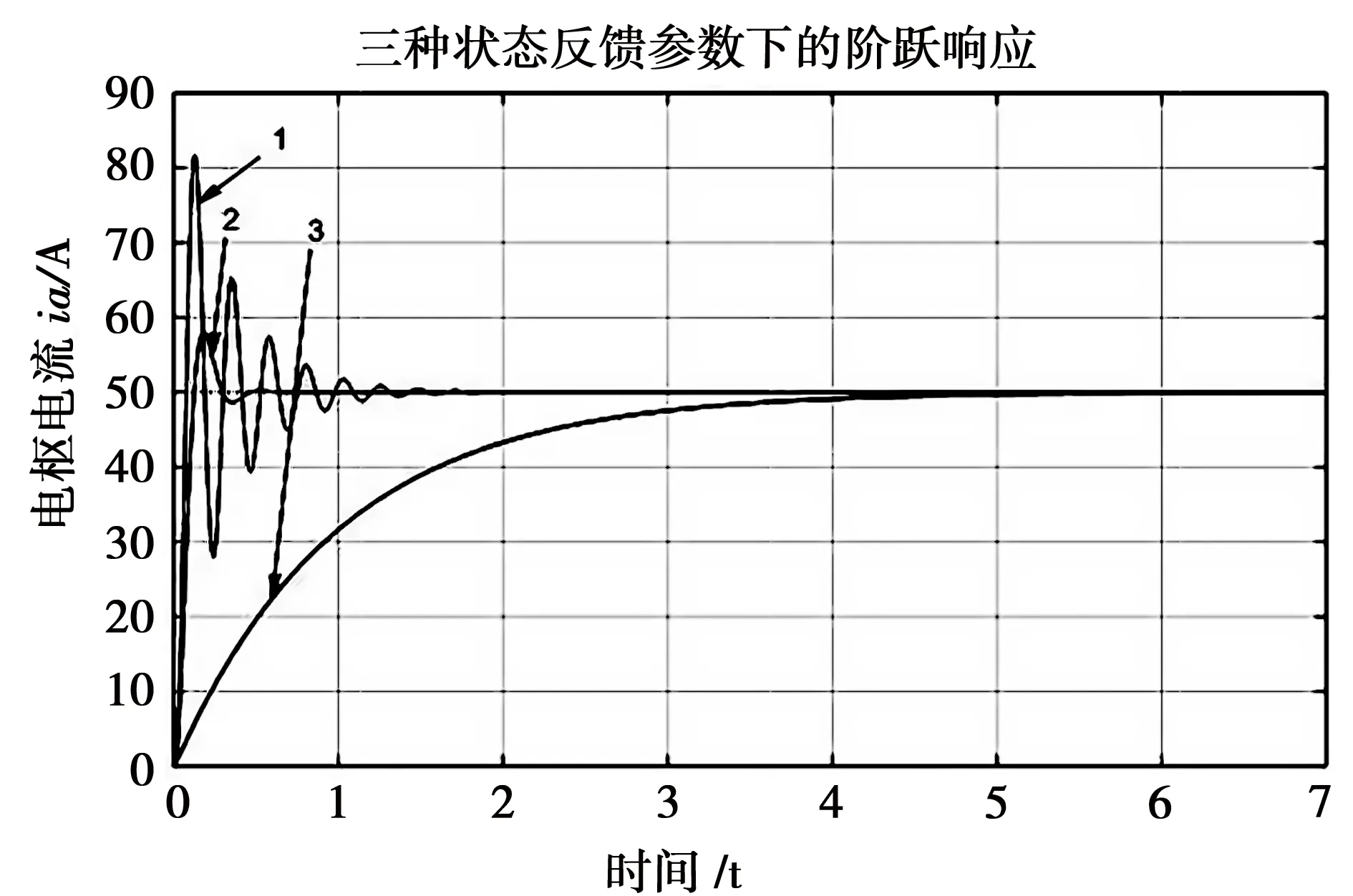
图8 三种状态反馈参数下的系统阶跃响应曲线

对三种状态反馈下的控制系统阶跃响应曲线进行分析，结果如下：

表1 三种状态反馈参数下的系统调速特性分析

因此应取第二组状态反馈系数：k1=0,k2=2 440.6,k3=77.3。

若将之反映到实际电路中则需要在原有控制回路中增加由集成运算放大器构成的状态反馈回路，并且将k1=0,k2=2 440.6,k3=77.3配置为放大倍数。但由于本文主要是做控制优化仿真，在此不做过多赘述。

5 结 语

本文针对国内外电动汽车普遍使用的双电机驱动系统的缺点，首先设计了一种带有增磁绕组的直流永磁同步电机驱动系统。然后，设计了一个针对该驱动系统带有“再生制动”回路的PID控制器，PID控制器使用了IGBT模块，该控制器精度满足实际要求，同时还能实现“再生制动”的工作过程，提高了电动汽车的续航能力。对该控制系统进行稳定性分析，发现其并不满足稳定性指标，需要进一步优化。在比较各种优化方法后，采用线性二次型算法进行优化。从MATLAB仿真结果来看，优化后的系统满足电动汽车工作的实际要求，同时相较于现有的驱动系统，兼具较长的续航能力，较好的再生制动效果，更好的控制精度和调速特性等优点，为电动汽车提供了一种更优的驱动系统及控制方案。