基于装夹变形的某车身侧围公差优化分配

范满珍， 宋龙龙， 曹 菁

(1.山东工业技师学院， 潍坊 261000； 2.山东科技职业学院， 潍坊 261000；3.山东交通职业学院， 潍坊 261000)

车身公差分配是指汽车在设计阶段按照一定的要求为各组成零部件分配合理的公差，公差分配是否合理直接影响到汽车的装配质量[1-3].由于车身薄板件具有易变形的柔性特点，所以在焊装过程中刚性夹具极易引起装夹变形，使得分配的公差产生较大偏差，因此，有必要对车身装夹变形进行研究以提高汽车装配质量.

目前，基于刚体假设的偏差分析方法已不能精确的分析柔性车身件的装配偏差，所以现在很多学者致力于研究基于柔体假设的偏差分析方法[4]，主要有：影响系数法[5]、有限元分析法[6]、柔性静态分析法[7]、多工位装配偏差分析法[8]等.本文在结合上述方法的基础上，提出了车身侧围装夹变形分析，并将装夹变形因素考虑到基于粒子群算法的公差优化分配中，最后，通过质量成本理论对结果进行了评价，结果表明优化后该车身侧围装配质量明显提高，验证了该公差优化分配方法的合理性.

1 公差优化分配模型

1.1 目标函数

车身侧围公差优化分配的合理性指标一般是以经济性为衡量标准，旨在以最低的制造成本为零件分配尽可能大的公差[9]，因此，公差优化分配的目标函数就是所有装配组成环的制造成本总和最小，记为制造总成本C,则有：

(1)

式中：n为装配组成环数；ωi为权重系数；Ci为第i个组成环的制造成本.

参考文献[10]采用零件加工特征尺寸代表零件尺寸，给出车身侧围孔及面特征的加工公差-成本模型：

(2)

(3)

式中：t为组成环的公差；C(t)为加工成本.

1.2 约束条件

车身侧围公差优化分配中，约束要素有：

(1)车身侧围装配公差约束.

(4)

式中：ti为第i个组成环的公差；λi为公差传递系数.

(2)车身侧围加工能力约束：

timin≤ti≤timax.

(5)

式中：timin、timax分别为允许的最小和最大加工公差.

2 车身侧围装夹变形分析

车身侧围焊装时，其首要工作是工件的定位装夹过程，图1所示为该车身侧围焊装定位夹紧模型.由于车身薄板件具有易变形的柔性特点，那么在焊装过程中,刚性夹具极易引起零件产生厚度方向的装夹变形，影响车身侧围公差分配，进而影响到汽车装配质量.

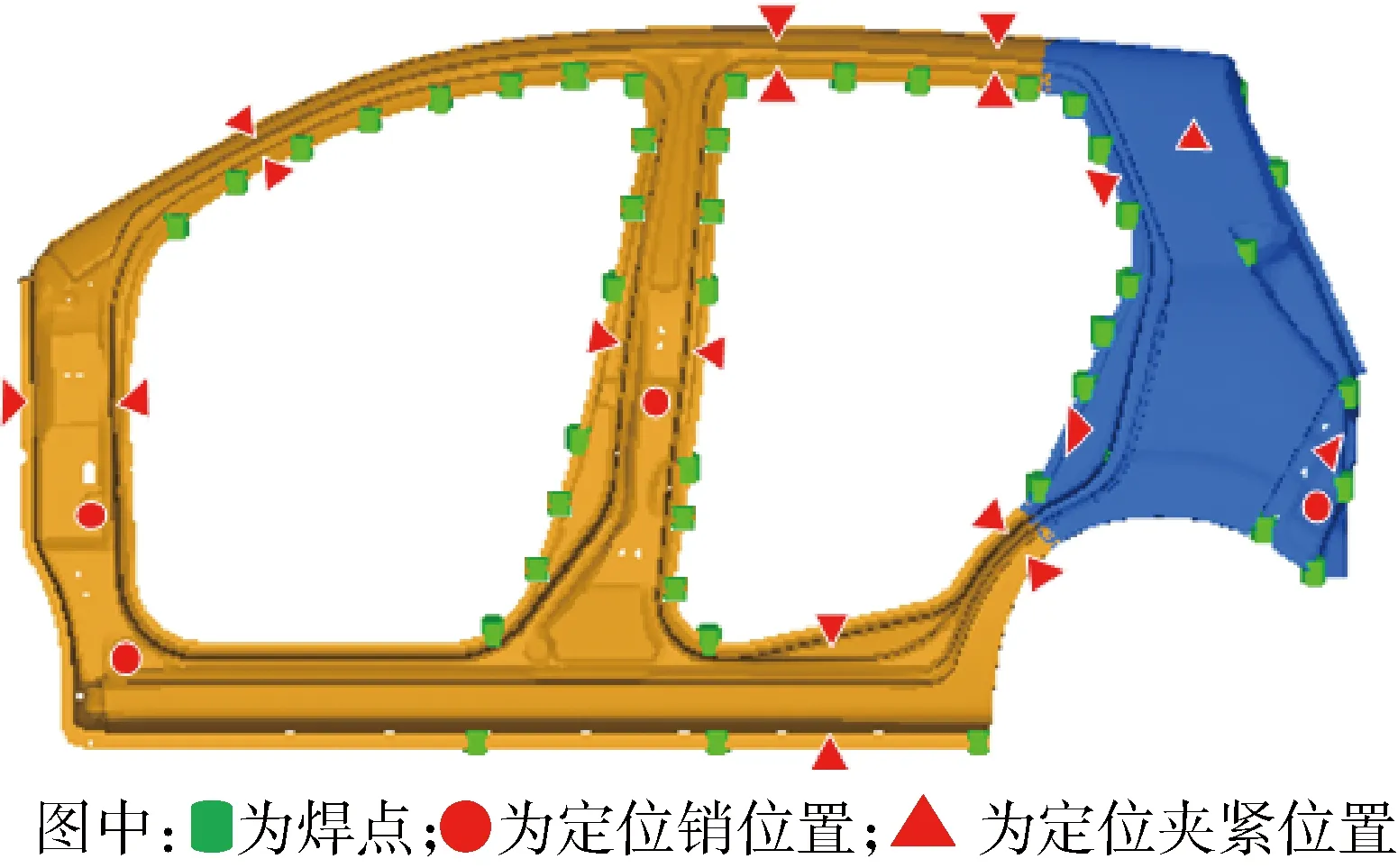
图1 车身侧围定位加紧模型

2.1 车身侧围有限元模型

该车身侧围(以左侧围为例)由侧围前端、侧围后段、侧围内板、后围连接板和侧围轮罩等组成.对该车身左侧围建立有限元模型，所有零件采用板壳单元离散，并尽量采用四边形板壳单元模拟，焊点采用Cweld单元模拟，钎焊采用单元耦合模拟，建立的有限元模型如图2所示.

图2 车身侧围有限元模型

2.2 分析结果

夹具引起的零件偏差可以通过关键点的三坐标(CMM)测量值与理论值的差值得到偏差大小，但是夹具夹紧力、焊枪电极力等大小不易测量，因此，通过位移约束描述力作用下的偏差是简单可行的，故在Hypermesh中采用位移约束来描述夹具引起的偏差，分别在焊点连接处和夹具定位点处施加已经测得的强迫位移，并通过NASTRAIN进行求解，求解结果如图3所示，根据6个测点建立局部坐标系，x轴垂直于侧围后段与后保险杠间隙方向，y轴沿着间隙方向，z轴沿侧围后段与后保险杠面差方向.

由图3可知，车身侧围最大位移位于侧围前端与后段的钎焊处，变形量约为0.541 mm，同时引起其他地方不同程度变形.钎焊应力引起的变形较大，符合实际侧围焊装过程的变形情况.文中旨在分析装夹变形对侧围后段和后保险杠偏差的影响，故在侧围后段等距离选取6个测点，分别测量测点在其x方向和z方向的位移量，即可得到侧围后段与后保险杠之间的间隙和面差变形量，统计其位移量结果见表1.

图3 车身侧围装夹变形分析结果

表1 测点位移量

测点x方向位移量/mmz方向位移量/mm1+0.120-0.0052+0.131-0.0073+0.148-0.0094+0.170-0.0105+0.192-0.0116+0.213-0.028

由表1可见，测点在x方向的平均位移量为+0.162 mm，变形较大，即装夹变形导致侧围后段与后保险杠间隙变大；z方向的平均位移量为-0.012 mm，变形很小，偏差数量级为10-2mm.在公差优化分配中起极小作用，可以忽略不计，即装夹变形对侧围后段与后保险杠面差基本无影响.因此，提出将装夹变形量作为约束条件添加到公差优化分配中，使得公差分配更加贴近实际装配情况，分配合理的公差.

3 某车身侧围公差优化分配

3.1 车身侧围公差分析

该车身侧围装配偏差集中在侧围后段与后保险杠的间隙和面差上，如图4所示.经现场检测排除了后保险杠引起偏差的可能，故为了简便，只以左侧围为研究对象.根据该型车身精度公差标准查得，图4中A处间隙理论值为0.65 mm，公差为0～0.5 mm；B处面差理论值为0 mm，公差为-1～0 mm.

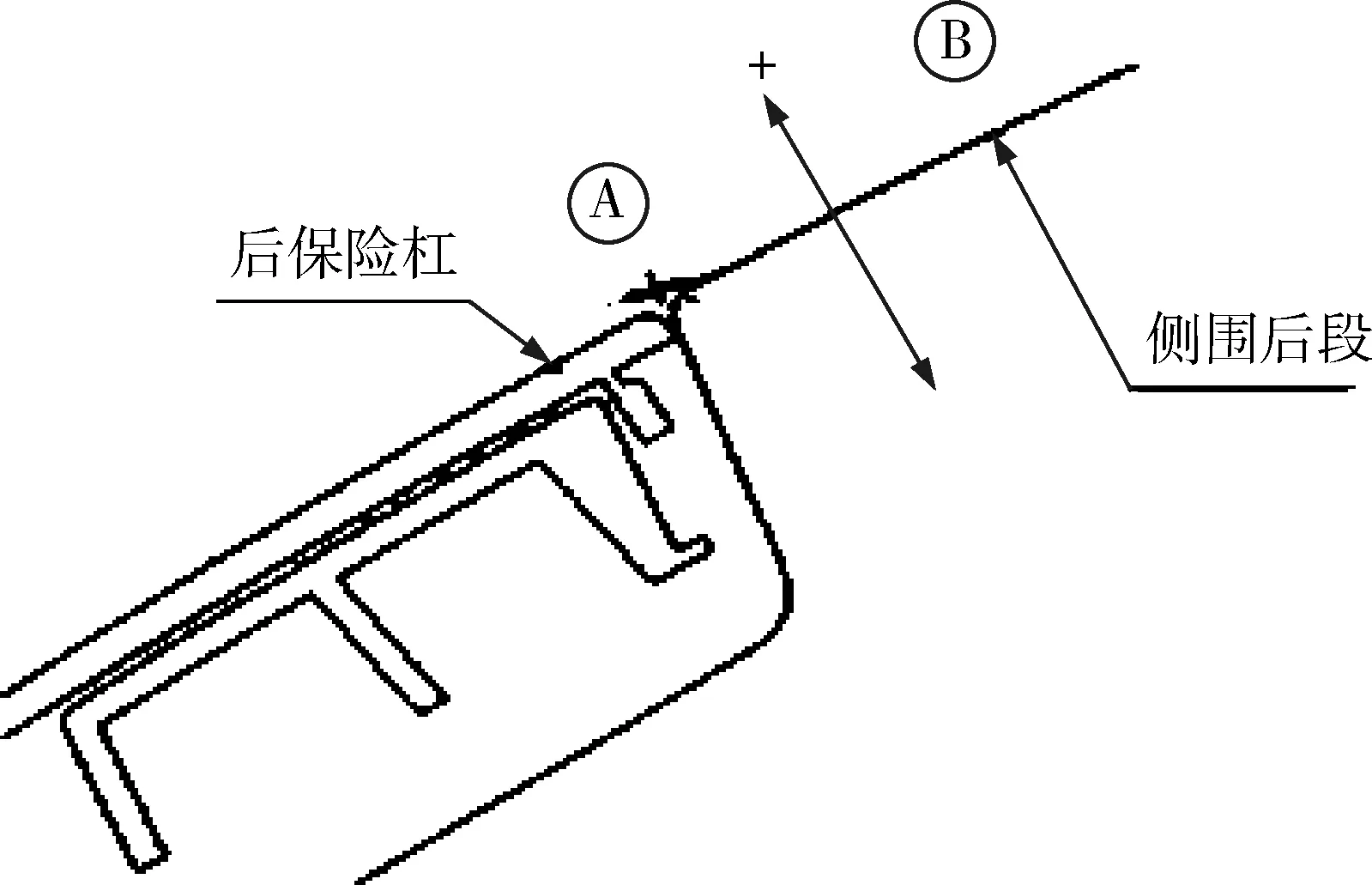
图4 侧围后段与后保险杠装配偏差

根据设计图纸设定车身侧围零件公差：定位面轮廓度0.3 mm，搭接面轮廓度0.7 mm，一般轮廓面1.0 mm，定位孔位置度0.2 mm，一般安装孔位置度0.6 mm.对上述6个测点设置测量，并基于3DCS进行虚拟装配偏差分析，分析侧围后段与后保险杠间隙和面差的偏差，3DCS分析结果见表2.

表2 3DCS分析结果

由表2看出，侧围后段与后保险杠的间隙和面差都有较大偏差，间隙的最大超差率达到23.32%，面差最大超差率为18.95%，均大于5%，不满足装配要求，因此，需要对超差率较大的零件重新添加约束条件进行公差优化分配.

3.2 基于装夹变形的公差优化分配

该车身侧围中，装配组成环由侧围后段后保险杠安装面、上下侧围搭接面和两个装配定位孔构成.

3.2.1 车身侧围组成环制造成本

minC=C(t1)+C(t2)+C(t3)+C(t4)+C(t5)，

(6)

式中：

ti(i=1～5)依次是侧围后段后保险杠安装面、上下侧围搭接面和两个装配定位孔的公差.

3.2.2 基于装夹变形的约束条件

由于装夹变形使得侧围后段间隙处平均变形+0.162 mm，导致间隙变大，而装夹变形在车身侧围装配中又是不可避免的，因此，认为装夹变形引起的变形量是固定的，那么装配间隙公差约束就相应的由理论值0.65 mm调整为0.488 mm.

车身侧围装配公差约束：

0.2t1+0.3t2+0.3t3+0.6t4+0.6t5≤0.488.

(7)

车身侧围加工能力约束：

0.1≤t1≤0.5;
0.1≤t2≤1.0; 0.1≤t3≤1.0;
0.1≤t4≤0.3; 0.1≤t5≤0.3.

3.2.3 优化结果

公差分配模型是一个比较复杂的非线性模型，常规的优化算法难以获得满意的优化结果，因此，文中采用算法效率较高的粒子群算法进行优化计算[11-12]，设置相关参数，粒子数为100，最大迭代数为100，在MATLAB中计算求解，计算结果如图5所示.

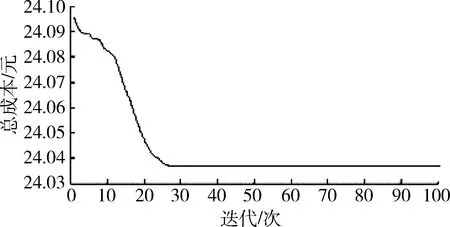
图5 优化计算结果

由图5可知，随着迭代增加，目标函数在迭代30次后趋于稳定，最终保持在最低成本24.04元，可见粒子群算法有较好的收敛性和计算效率，得到的最优解ti(i=1～5)依次为0.252 1 mm、0.615 7 mm、0.620 3 mm、0.152 2 mm、0.150 2 mm.

由最优解结果可见，将装夹变形因素考虑到车身侧围装配约束条件后，零件公差得到优化.根据求解结果并结合企业加工条件调整侧围后段后保险杠安装面公差为0.25 mm、上下侧围搭接面公差为0.6 mm，装配定位孔公差为0.15 mm，最后基于3DCS验证公差优化分配结果，结果见表3.

表3 3DCS验证结果

比较表2和表3结果可见，基于装夹变形因素进行公差优化分配后，侧围后段与后保险杠的间隙和面差超差率明显降低，均小于5%，满足装配要求，车身侧围装配质量大大改善.

3.3 质量成本评价

基于装夹变形公差优化分配后，车身侧围零件公差降低，汽车装配质量明显提高，但相应的制造成本也会增加，因此，文中基于田口质量的质量成本理论[13-14]，通过总损失函数W(x)，即制造成本函数C(x)与质量损失成本函数L(x)之和，来衡量产品质量和制造成本之间的矛盾，总损失成本函数如式(9)所示.

(9)

式中：x为产品输出特性指标；k为质量损失系数.

根据公式(9)计算公差优化分配前后总损失成本，比较结果见表4.

表4 总损失成本比较

由表4可见，该车身侧围公差优化分配后，制造成本由22.625元增加到24.040元，增加了6.25%，质量损失成本由16.981元减少到12.733元，减少了25.03%，总损失成本减少了7.16%，验证了该公差优化分配方法的合理性，兼顾了企业和顾客的利益，既保证了产品质量，又减少了给用户带来的损失.

考虑装夹变形因素对车身侧围进行公差优化分配后，间隙和面差的公差超差率均降低到5%以内，装配质量明显提高，采用粒子群优化算法保证了最低制造成本24.04元，并且总损失成本降低了7.16%，验证了该公差优化分配的合理性.因此，基于装夹变形的公差优化分配能合理的平衡汽车装配质量和制造成本之间的矛盾，实现以较低的制造成本提高汽车装配质量的优化目标.

4 结 论

1)基于装夹变形对该车身侧围公差优化分配后，侧围后段与后保险杠的间隙和面差公差超差率由20%左右降低到5%以内，装配质量明显提高，可见考虑装夹变形因素能更加贴近实际装配情况，分配合理的公差，有效提高了汽车装配质量和精度.

2)该车身侧围公差优化分配后，采用质量成本理论对其结果进行评价，结果表明总损失成本降低了7.16%，验证了该公差分配方法的合理性，既降低了成本，又提高了汽车装配质量，同时为均衡企业制造成本和顾客质量损失之间的矛盾提供一定参考.