永磁同步电动机矢量控制系统谐波电流抑制

孙 健， 王爱元， 王 涛， 金永星

(上海电机学院 电气学院， 上海 201306)

由于新型优质稀土永磁材料及电力电子技术和智能化控制器的出现，推动高功率和高频率开关的电子器件的研发与应用，永磁同步电动机(Permanent Magnet Synchronous Motor, PMSM)在诸多领域内得到推广，例如高性能中小功率的调速电动机和伺服电动机在智能控制、汽车驱动、风力发电、航天航空、智能设备等领域推广应用。永磁同步电动机本身具有控制方法简单、转矩惯性比大、动态响应好、功率密度高、结构紧凑、效率高等优势，不过由于受电动机本体磁极结构[2-3]、定子槽型[4]等结构的影响，会导致电动机磁场产生畸变。同时，受电路非线性因素如驱动控制器固有管压降和死区时间的影响[5-6]，PMSM三相电流中出现谐波量。而谐波会加重电动机损耗，影响散热，产生振动和噪声，加重带载不稳定性。因此，谐波电流抑制是优化PMSM服役能力的关键。

就PMSM谐波问题来说，诸多文献从以下两点进行解决：① 从本体结构考虑，优化定、转子齿槽结构，消除反电动势波形畸变。② 从电动机控制策略及算法的角度，对电动机控制模块的逆变装置进行设计改进。文献[4]针对逆变装置中绝缘栅双极型晶体管(Insulated Gate Bipolar Transistor, IGBT)频繁的开通与关断过程产生的诸多5、7次高频谐波电流，提出了一种改进的电磁干扰(Electro Magnetic Interference, EMI)滤波器来消除干扰电流量，阻断电磁干扰信号的通讯途径，以抑制PMSM的谐波电流。然而，EMI滤波器的应用过程需要选择恰当的频率截止值来消除高频率干扰源。对于干扰源有范围要求，EMI滤波器在应用中具有局限性。文献[5]针对脉冲宽度调制(Pulse Width Modulation, PWM)供电系统谐波含量大对电动机性能影响较大的问题,借助Maxwell建立电动机仿真模型,借助Simplorer建立电动机控制模型,通过设置联合仿真接口实现了电磁场数值分析，并提出通过3次谐波注入来补偿谐波，减小电动机的转矩脉动，虽然联合仿真具有良好的动态性能且实现5、11、19次谐波抑制的效果，但3次谐波注入会引入其他的高次谐波。文献[7]通过在控制器中加入前馈环节的方法来补偿抑制逆变装置固有的死区带来得5、7次谐波分量，但忽略了抑制其他因素导致的谐波电流方法的应用。文献[12]提出新颖的电流调节器，它将采用比例、积分和谐振环节复合利用。虽然谐波电流得到削弱，但谐波不同分量之间会形成交叉干扰，对系统稳态性能不利。

针对上述文献的不足，在研究谐波产生机理的同时，提出了基于PMSM矢量控制系统的谐波电流抑制算法。通过引入谐波电流环节来补偿逆变器引入的谐波电流，提高PMSM的电流波形以实现稳定运行。

1 PMSM谐波数学模型

PMSM处于正常运行状态，由于气隙磁场分布不均匀、逆变装置的非线性特征造成电动机电流波形正弦度差、谐波含量高。而谐波中含有的5、7次谐波对电动机运行性能的影响占比较重。因此，本文针对5、7次谐波推导PMSM谐波数学模型。

PMSM端口电压在dq旋转坐标系下的稳态方程为

(1)

式中：ud、uq分别为d、q轴电压；Ld、Lq分别为d、q轴电感参数；id、iq分别为d、q轴电流；ψf为电动机永磁体磁链；Rs为定子电阻；ω为基波电压的角速度。

PMSM是通过对称三相系统供电。在忽略实际损耗参数影响的工况下，只含有正常基波量，其转化到dq坐标下的电压、电流均表现为直流量。而在实际运行中，电动机电压中不可避免地有谐波分量存在，此时，d、q电压电流为一系列交流量。

对于PMSM供电系统，其定子绕组的n次三相谐波电流各相之间存在2nπ/3相位关系如下:

(2)

式中：ian、ibn、icn分别为a、b、c三相的n次谐波电流；Im为谐波电流幅值；αn为谐波电流的初相位。

对于式(2)，当n分别为3k、3k-1、3k+1(k=1,2,…,n)时，其电流的相位关系存在差别。由于PMSM定子绕组电流中包含5、7次谐波，其中5次电流谐波向量相位关系与基波相同，而7次谐波向量相位关系与基波相反。所以，该电流量可以表示为

(3)

式中：I1m、I5m、I7m分别为三相基波、5、7次谐波电流幅值。

对于永磁同步电动机三相谐波电压也存在式(3)的相位关系，利用幅值不变约束下的坐标变换，将PMSM三相电压、电流量作abc/dq坐标系变换得：

(4)

(5)

式中：ud1、uq1分别为电压基波量经abc/dq变换后在基波下的交直轴分量；id1、iq1分别为电流基波量经abc/dq变换后在基波下的d轴、q轴分量；i5、i7分别为5、7次谐波电流的幅值；α2、α3、α5、α6分别为5、7次谐波电压、电流的初始相位。5、7次谐波由a、b、c三相静止坐标系变换到基波dq同步旋转坐标系，转变成6次谐波。

修改式(1)中uq项，令u′q=uq-ωψf，可得：

(6)

在dq同步旋转坐标系中，5、7次谐波矢量相对于基波矢量旋转速度和方向分别为-5ω、7ω。则式(5)代入式(6)可得：

(7)

依据abc/dq变换方法，对于任一频率谐波矢量映射到此频率所在的dq坐标轴系下，其矢量可被看作直流量。如5次谐波矢量在5次dq坐标轴系下，其对应为直流量，而基波和其他次谐波(5次谐波除外)均对应为正弦交流量。将式(7)分别变换到5、7次dq坐标轴系下，同时忽略每项方程中的交流成分，获得5、7次dq谐波稳态方程式分别为

(8)

(9)

式中：id5、iq5为在5次dq坐标轴系下5次谐波电流的幅值；id7、iq7为在7次dq坐标轴系下7次谐波电流的幅值。

2 谐波抑制策略

图1所示为PMSM谐波电流抑制系统框图。

为了使PMSM电流谐波得到有效控制，在采用Id=0控制方式，内环为电流环，外环为转速环的PMSM调速系统中，通过嵌入谐波电流环节来实现谐波电流最小化控制。

图1中，ω*为速度给定；udc为直流母线电压。

图1 PMSM谐波电流抑制系统框图

电动机三相电流ia、ib、ic被采集后输入PMSM调速控制系统后获得u′a、u′b、u′c，输入谐波电流环节得到的u″a、u″b、u″c。二者叠加后输出ua、ub、uc，然后将其放入PWM控制设备输入端口转换为逆变装置的6路驱动源。

其中，谐波电流提取模块通过采集电动机实际三相电流后，经坐标变换及低通滤波器输出5、7次dq轴谐波电流，如图2所示。

图2 5、7次谐波电流提取模块

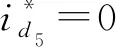
图3 谐波电流抑制模块

3 仿真实验分析

为了上述控制策略的合理性，利用Matlab/Simulink软件构建各个控制环节进行实验验证。表1给出了所涉及的样机及逆变装置参数，系统将PMSM转速设定为900 r/min并进行仿真实验。图4、图5分别为PMSM加入抑制谐波算法前后的三相电流波形。

表1 样机及逆变装置参数

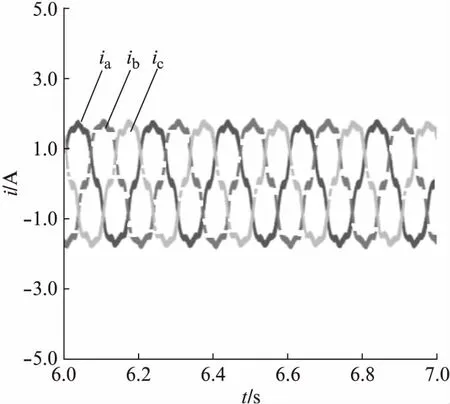
图4 未加入谐波抑制算法三相电流波形

图5 加入谐波抑制算法三相电流波形

对比图4、图5可知，图4未加入谐波抑制算法的abc三相电流波形失真明显、正弦度差，在电流幅值过零处出现波形箝位，同时电流正负向峰值处存在下陷；图5控制系统添加抑制策略后，PMSM三相电流得到明显变化，波形峰值附近脉动消失，获得良好的正弦波形。图6所示为谐波抑制前后PMSM仿真模型电流a相的各频率分布情况。由图6可知，5次谐波含量百分比由7.56%降至3.79%，7次谐波含量百分比由6.21%降至2.31%，说明所加算法对谐波抑制有效。

图6 抑制前后a相电流频谱

4 结 论

本文就PMSM正常工作中的谐波抑制问题，通过相关理论推导及仿真分析获得如下结论：

(1) 通过仿真波形可知，本文提出的5、7次PMSM谐波数学模型能够有效抑制谐波电流，提高波形正弦度；

(2) 对于PMSM驱动系统的固有非线性因素带来的电流谐波，在原有矢量控制系统的电流控制环节中增加谐波电流抑制模块，可以实现削弱系统中谐波电流的目的。