接触模式对球床堆有效导热系数影响的数值分析
步珊珊,陈波,田兴,孙皖,马在勇,张卢腾
(重庆大学低品位能源利用技术及系统教育部重点实验室,400044,重庆)
球床堆在核能领域中有较多的应用,比如高温气冷球床堆[1]、熔盐球床堆[2]和聚变增殖球床包层[3]等。球床堆的有效导热系数表征了球床堆芯的宏观传热能力,是反应堆热工设计和安全分析程序中的基本参数,其主要由固体表面间的辐射、球体颗粒的导热和流体的导热、相邻颗粒接触点之间的接触导热[4]等3个部分组成。在事故工况下,当冷却剂失去强制流动后,堆芯冷却剂的雷诺数很小,对流传热不考虑。
目前,关于有效导热系数的研究主要集中于理论分析[5]和实验研究[6],基于孔隙尺度的数值研究还较少。孔隙尺度的数值方法可以获得球床堆局部孔隙速度和温度分布,通过逆求解导热微分方程得到有效导热系数。球床堆颗粒之间的接触导热是球床堆有效导热系数中的重要组成部分,基于孔隙尺度的数值分析中,颗粒之间的接触区域网格控制比较困难,通常需要对相邻颗粒接触区域做一定的简化[7],目前常采用间隙模型[8]、面接触[9]和短圆柱模型[10]这3种方法简化接触区域。因此,在数值分析中,相邻颗粒接触区域的简化处理会影响有效导热系数的计算。
为了数值分析接触区域的简化方法对球床堆有效导热系数的影响,本文首先采用间隙模型分析了不考虑接触导热下的球床堆有效导热系数,然后采用面接触和短圆柱模型分析了考虑接触导热下的球床堆有效导热系数,最后分析了不同温度下接触模式对球床堆有效导热系数的影响。
1 物理模型
本文首先研究了不考虑接触导热下3种有序球床堆的有效导热系数,然后研究了接触区域处理方式对简单立方结构球床堆中有效导热系数的影响。3种有序球床堆的结构包括简单立方结构(SC)球床堆、体心立方结构(BCC)球床堆和面心立方结构(FCC)球床堆。对于有序堆积结构的球床堆而言,堆积结构本质上是周期性的,因此为了简化模型和减少计算量,可以采用部分几何堆积单元结构来研究球床堆的有效导热系数,如图1所示。

(a)SC (b)BCC (c)FCC图1 3种有序球床堆示意图
本文中球颗粒的直径dp为2 mm。当不考虑接触导热时,球体直径减小为原来直径的99%,可以看作是间隙模式;当考虑接触导热时,由于相邻球形颗粒的接触点区域网格生成很难控制,采用面接触模式和短圆柱接触模式来简化接触点区域。3种不同的接触模式如图2所示。面接触模式的生成方法分为两种:方法一是球体位置不变,将球体直径扩大使得球体接触;方法二是球体直径不变,改变球体位置使得球体接触。考虑到接触半径rc对传热的影响[11-12],又分别考虑了两种不同接触半径下的面接触模式和3种不同接触半径下的短圆柱接触模式,因此本文计算模型一共有8种,如表1所示。

(a)间隙模型 (b)短圆柱接触模式 (c)面接触模式图2 3种接触模式示意图

模型结构dp/mm孔隙率/%接触模式rc·d-1p/%SC1.9849.2间隙BCC1.9834.0间隙FCC1.9828.2间隙SC2.0047.6短圆柱8SC2.0047.6短圆柱2.5SC2.0047.6短圆柱1.75SC2.0246.1面接触7.1SC2.0046.4面接触6.3
2 数值计算方法
本文以ANSYS Fluent14.5为计算平台,基于有限容积法对能量方程进行求解。边界条件如下:在模型z方向(热流传递方向)的前后两个面是定温边界条件,前后面的温差为10 ℃。垂直于xy平面的4个表面是绝热的。球体材料为钛酸锂,孔隙中充满氦气,球体和氦气的接触面实施无滑移条件,假定热流和温度的连续性。求解器选择基于压力求解,气体与固体接触面设置为COUPLED,求解算法为SIMPLE。离散格式采用二阶迎风格式。固体和流体的导热系数随温度变化[4],通过一维傅里叶导热定律来计算有效导热系数
(1)
式中:q是平均表面热流量;ΔT是沿热流方向的温度差。本计算中流体无流动,只需要求解固体区域和流体区域的能量方程。计算工况是稳态,且球床内无内热源,物性参数是温度T的函数,因此流体和固体区域的能量方程为
(2)
式中k是固体或者气体的导热系数。
采用ICEM对几何模型进行非结构化网格划分,接触区域进行适当的加密。面接触模式下固体颗粒表面、固体区域和气体区域的网格如图3所示。网格无关性考核如表2所示,4套网格单元总数分别为6 979 463、5 986 267、4 794 363和2 735 315。结果表明,当球床平均温度为500 ℃、网格数为6 979 463和5 986 267时模型计算所得的有效导热系数相差很小,可以认为网格总数为5 986 267时获得网格无关解,其在球体或流体区域和球体接触区
(a)颗粒表面网格 (b)固体区域和气体区域网格图3 面接触模式下网格划分示意图

网格数平均热流密度/W·m-1有效导热系数/W·m-1·℃-1相对误差/%6 979 4632 1470.859 05 986 2672 1460.858 60.044 794 3632 1420.856 80.252 735 3152 1400.856 10.34
的最大网格特征长度分别小于0.1 mm和0.05 mm,其余计算模型也采用类似网格进行计算。
3 计算结果与分析
3.1 不考虑接触导热时的有效导热系数分析
采用间隙模型分析不考虑接触导热时的计算结果,先将计算结果与不考虑接触导热的ZS关联式[13]结果比较,如图4所示。ZS关联式如下
(3)
(4)
(5)
式中:ks是固体的导热系数;kg是气体的导热系数;B是球床的形变参数,与孔隙率有关;ε是球床堆的孔隙率。
从图4可以看出:球床堆的有效导热系数随着温度升高而增大,3种堆积结构下的球床堆计算结果与ZS关联式结果的差别很小,而且趋势走向基本一致。与ZS关联式相比:SC球床堆的有效导热系数最大误差为1.5%;BCC球床堆的有效导热系数最大误差为3.9%;FCC球床堆的有效导热系数最大误差为2.3%。同时,可以看出相同温度下,FCC球床堆的有效导热系数最大,SC球床堆的有效导热系数最小。这是由于固体导热系数比气体导热系数大,孔隙率越小,固体填充率越大,球床堆的有效导热系数越大。综上所述,在不考虑接触导热时,间隙模型下的球床堆计算模型的计算结果能较好地预测球床堆的有效导热系数。

图4 不考虑接触导热时计算结果与ZS关联式结果对比
3.2 考虑接触导热时的有效导热系数分析
本文考虑接触导热时,采用面接触和短圆柱接触模式来简化接触点区域的计算模型。采用Kaviany关联式[5]计算球体接触区域导热系数模型,与ZS关联式叠加后可以获得考虑接触导热下的球床堆有效导热系数ZSK关联式。Kaviany使用赫兹弹性形变原理,提出的计算球体接触区域导热系数模型如下
(6)
(7)
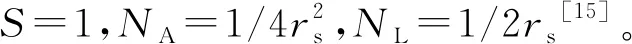


图5 面接触模式计算结果与ZSK关联式结果对比


(a)大接触半径
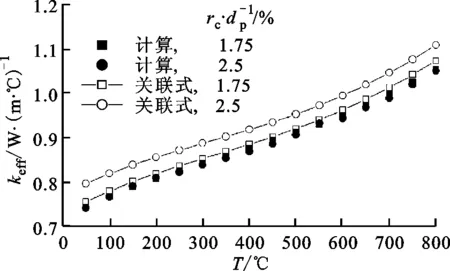
(b)小接触半径图6 短圆柱接触模式计算结果与ZSK关联式结果对比
3.3 不同温度下接触模式对球床堆有效导热系数的影响
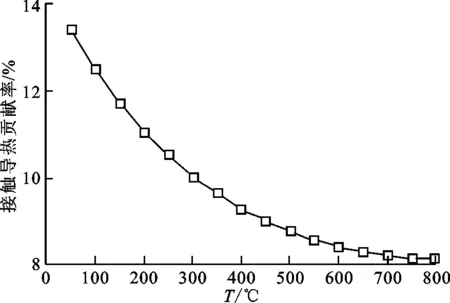
图7 接触导热对球床堆有效导热系数的贡献
在不考虑辐射的情况下,不同温度下接触导热对球床堆有效导热系数的贡献如图7所示,随着温度的升高,接触导热占有效导热系数的份额不断降低,但是降低的趋势逐渐变缓。接触导热对有效导热系数的贡献最大为13%,当温度达到800 ℃时,接触导热的贡献只占8%左右。这是由于当流体静止时,球床堆的导热系数主要受固体颗粒和气体颗粒的导热性能影响,氦气的导热系数随温度升高而增大;当温度小于550 ℃左右时,固体颗粒材料Li2TiO3的导热系数随温度的升高而减小,然后随温度升高而增大,如图8所示。在高温下,如果考虑到辐射,接触导热对有效导热系数的贡献还会进一步降低,因此随着温度升高,接触模式对有效导热系数的影响会减弱。低温下接触模式对球床堆有效导热系数的计算结果影响会比较显著,高温下接触模式对球床堆中有效导热系数计算结果的影响会显著减小。

图8 球床堆堆积颗粒和气体的导热系数
4 结 论
本文主要数值分析了颗粒接触模式对球床堆有效导热系数的影响,主要工作和结论如下。
(1)在不考虑接触导热时,间隙模型下的球床堆计算模型的计算结果与ZS关联式结果吻合很好。
(2)当考虑接触导热时,由于受网格质量限制,面接触计算模型的接触半径较大,因此计算的球床堆有效导热系数与ZSK关联式结果相比误差较大;在网格生成质量允许的情况下,推荐使用较小接触半径的短圆柱接触计算模型。
(3)低温下,接触模式对球床堆有效导热系数的计算结果影响不能忽略;高温下,接触模式对球床堆有效导热系数计算结果的影响会显著减小。

