潜水搅拌器安装角度对盐泥水洗搅拌效果的影响
朱桂华,彭南辉,张傲林,巴赛,唐浩亭
(1.中南大学机电工程学院,410083,长沙;2.中南大学高性能复杂制造国家重点实验室,410083,长沙)
矿井盐卤水净化工艺产生大量盐泥。为有效减少盐泥中氯化钠含量,对盐泥进行水洗搅拌。盐泥中残留卤水体积占比小,且与水洗剂传质速率快,水洗搅拌可近似看作不存在传质过程的搅拌混合,而传统大型立式搅拌桨存在能耗需求大,流场可塑性差的不足[1],因此本文提出将潜水搅拌器应用于盐泥水洗搅拌的新思路。
搅拌混合的研究关键点是以最短的混合时间、最少的单位体积混合能获得所需要的混合效果。目前计算流体力学(CFD)凭借成本低、周期短以及适应性强等优势已逐渐用于流体混合过程的数值研究。Daoelo等用CFD分析了混合设备内气体搅拌过程,结果表明模拟得到的速度场和剪切速率与实验结果吻合[2]。Lane等研究滑移网格法和MRF法对混合过程模拟的有效性,得出MRF法计算成本低、模拟结果有效的结论[3]。张晓宁等用CFD分析了单潜水搅拌器布置角对搅拌流场的影响,得出布置角为45°时流场较好的结论[4]。施卫东等对比不同形状搅拌槽内潜水搅拌器的三维流场,表明采用渐进圆管、圆直管搅拌槽节能效果显著[5]。Wray等研究表明,大型叶片式潜水搅拌器所需功率仅为小型叶片混合器的1/4[6]。
以往的研究均针对潜水搅拌器的搅拌流场,而本文以两相混合时流速场、混合时间、单位体积混合能、盐泥体积分数标准差、湍动能和湍动能耗散率为指标,对双潜水搅拌式水洗设备内潜水搅拌器安装角度进行优选,可为制盐工业盐泥的高效预处理提供一定的理论依据。
1 双潜水搅拌式水洗设备
1.1 结构设计
双潜水搅拌式水洗设备主要包括斜底圆罐和沿罐体xoy面两侧安装的两个潜水搅拌器,该水洗设备额定处理量为每次40 m3,罐体半径R为3 500 mm,高度H为2 800 mm,底面倾角θ为2.5°,M、N点分别为圆罐斜底最高点和最低点。两个潜水搅拌器均为某公司生产的QJB型无导流罩式潜水搅拌器,叶轮半径r为310 mm,额定转速为480 r/min,如图1所示。根据工程实际与以往的研究,对池底进行射流冲刷,防止池底固体颗粒沉降,潜水搅拌器Ⅱ的叶轮外径至池底为100 mm,安装高度h2为410 mm,潜水搅拌器Ⅰ的安装高度h1为1 850 mm,两潜水搅拌器至罐体内壁安装距离L均为750 mm,两潜水搅拌器壁面安装点C、D在y轴方向正投影C′、D′的圆心角β为60°,两潜水搅拌器异面轴线的空间夹角为安装角度α。
1.2 工作原理

(a)主视图

(b)俯视图图1 斜底圆罐双潜水搅拌式水洗设备三维模型
水洗时,先向罐体内A2区域输送40 m3的盐泥,再向A1区域泵送水洗剂定容至100 m3后,两潜水搅拌器同时工作使盐泥和水洗剂混合均匀,经重力浓缩后,将盐度较高的上层溶液排出,剩余盐泥即为低盐度盐泥。本文设定安装角α分别为0°、5°、10°、15°、20°、25°、30°、35°和40°。
2 数值模拟
数值模拟所用的几何模型尺寸与双潜水搅拌式水洗设备尺寸完全相同。为简化分析,并能反映出双潜水搅拌式水洗设备的搅拌规律,假设两潜水搅拌器开始工作时,盐泥-水洗剂上下分层明显,忽略泵送水洗剂时水洗剂对罐体下层盐泥的扰动,数值模拟过程不考虑系统温度变化带来的影响。数值模拟将盐泥视为示踪剂,示踪剂体积分数检测点分别取如图2所示的48个监测点P1~P48,部分监测点坐标如表1所示。

图2 监测点设置

m
2.1 基本方程
流体的流动遵循质量守恒定律和动量守恒定律,3个控制方程[7-8]如下。
相体积分数守恒方程
(1)
动量守恒定理

(2)
连续性方程
(3)
式中:φq为q相体积分数;ρq为q相密度;vq为q相速度;p为各相共同承受的压力;τq为q相应力-应变张量;g为重力加速度;Rkq为各相之间相互作用力;mkq为k相向q相的质量传递;mqk为q相向k相的质量传递;vqk、vkq为相间速度;F为外力;Flift,q为升力;Fw l,q为壁面润滑力;Fvm,q为虚拟质量力;Ftd,q为湍流分散力;Sq=0为源项。
2.2 计算方法
本文研究的双潜水搅拌式水洗设备内两台潜水搅拌器形状复杂,旋转轴线与罐体轴线不重合,且罐体为不规则斜底罐,因此在ICEM中采用四面体非结构网格[9]对流体域进行划分。经网格无关性验证,计算各方案动区域的速度大小及搅拌器功率准数的改变量均不超过3%,最终确定采用158万个左右的网格进行划分,数值模拟过程采用Fluent 17.0进行瞬态计算。在固液混合过程潜水搅拌器叶片与罐体存在相对运动,而滑移网格法、动网格对计算机要求较高,故采用多重参考系法(MRF)对其进行模拟[10-11]。不考虑自由液面的影响,把自由液面设为对称边界条件[12],两搅拌叶轮设为旋转壁面边界,给定转速为480 r/min,罐底、罐壁均设为固定壁面条件,选用标准k-ε模型,Euler-Euler法中Euler模型对两相混合进行模拟[13-15]。采用标准初始化法对两相混合体系进行初始化,一阶迎风格式对湍流耗散率和湍动能方程进行离散,应用Phase Coupled Simple算法进行压力耦合求解,迭代过程开始部分时间步长设为0.01 s,后续为加快收敛速度,适当加大时间步长,计算残差设置为1×10-4。
对各方案进行数值模拟时,本文采用定体积法控制各混合相以及总混合体系的体积均对应相同。固液两相流中搅拌介质第一相为水洗剂相,密度为998.2 kg/m3,黏度为1.003 mPa·s,初始体积为60 m3;第二相为盐泥相,初始体积为40 m3,平均粒度为12.4 μm,密度为1 400 kg/m3,黏度为84.9 mPa·s。
3 模拟分析
3.1 流速场
双潜水搅拌式水洗设备内不同截面的流速云图如图3所示。由图3可知,各安装角度下的搅拌流速场均不具对称性,近潜水搅拌器流体域中高流速区占比较大,流动较为紊乱,这是由于潜水搅拌器出口端的液体运动是不同于正常层流或紊流的旋动射流,且旋动射流与水洗设备侧壁发生碰撞后发生冲击射流现象[16],使罐体近壁面流体域处流速增大。安装角α为0°,5°、20°时整个流体域内低流速区占比较小;α为10°,20°,30°、40°时在远离搅拌器的下游处流速较高;α为20°、40°时远离搅拌器的下游处流速稳定;综合考虑,安装角为20°时整个流体域内低流速区占比小,远离搅拌器的下游处流速较高且分布均匀,利于水洗剂和盐泥的混合。

α=0° α=5° α=10°

α=15° α=20° α=25°

α=30° α=35° α=40°图3 不同截面的流速云图
3.2 安装角对混合效果的影响
水洗搅拌设备宏观流动产生扩散的主体为对流扩散,常用混合时间、混合时间数、单位体积混合能和体积分数标准差来表征混合特性。微观流动产生扩散的主体是旋涡运动造成局部范围内的涡流扩散,湍动能、湍动能耗散率是决定微观混合的关键参数[17]。本文对混合效果的评价主要由混合时间t95、混合时间数Tm、单位体积混合能Wr、体积分数标准差σ、湍动能k、湍动能耗散率ε这5个方面来探讨。
3.2.1 安装角对混合时间的影响 根据95%原则[18],示踪剂的体积分数与最终稳定体积分数误差为5%时,即认为混合均匀,此时所用的时间即为混合时间,本文取各模拟方案下48个监测点混合时间的最大值作为该水洗设备的混合时间。根据数值模拟结果,可知水洗设备各安装方案时的混合时间t95,如表2和图4所示。由图4可知,α为20°时,t95最短为210 s,α为5°时,t95最长达437.2 s,考虑到混合时间,安装角选为20°。

表2 安装角对混合效果的影响
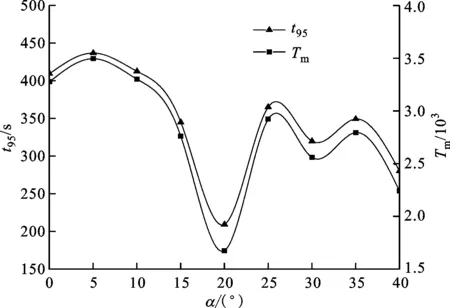
图4 混合时间和混合时间数随安装角的变化曲线
3.2.2 安装角对单位体积混合能的影响 单位体积混合能为
Wr=PrTm
(4)
(5)
Tm=Nt95
(6)
式中:Pr为单位体积搅拌功率,W/m3;N=8 r/s为两潜水搅拌器的转速;M为搅拌轴承受的扭矩,N·m;V=100 m3为水洗设备总体积。Wr越小,则表明搅拌损耗的能量越低。
双潜水搅拌式水洗设备内有两个潜水搅拌器,单位体积混合能为两个潜水搅拌器单独工作时单位体积混合能的代数叠加,不同安装角下单位体积搅拌功率、单位体积混合能如图5、图6所示,可知单位体积搅拌功率和单位体积混合能均不是恒定值,且搅拌时间响应曲线都是前期轻微振荡过后最终趋于平稳。α为0°时Pr最大,α为5°时Wr最大,α为35°时Pr最小,α为40°时Wr均较小,表明α为40°时节能效果最佳,安装角选为40°。

图5 不同安装角下单位体积搅拌功率
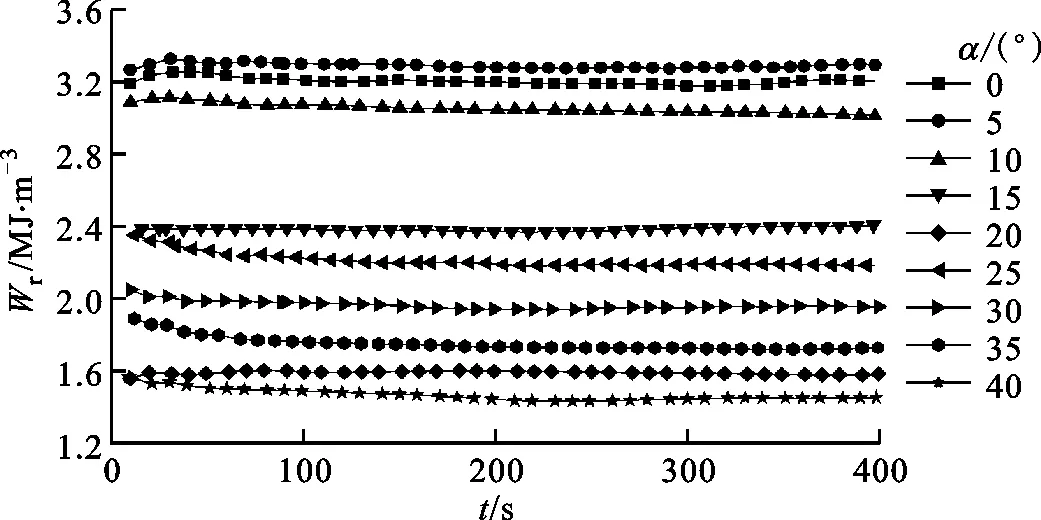
图6 不同安装角下单位体积混合能
3.2.3 安装角对盐泥体积分数标准差的影响 盐泥体积分数标准差σ越小,表明混合越均匀,安装角与盐泥体积分数标准差的关系曲线如图7所示。由图7可知,α为30°时σ=11.185×10-3为最大,α为20°时σ=4.868×10-3为最小,此时的混合均匀性最好,这是由于流体在潜水搅拌器叶轮的作用下沿搅拌轴轴向推进,并向径向扩散所致。轴向推流和径向扩散流碰到罐壁时发生反射,轴向有效推进距离和径向有效扰动半径均有所不同,使搅拌槽内的循环流或大或小,最终盐泥在搅拌槽内的波动较大,混合均匀性存在明显差异,考虑到混合均匀性,安装角选为20°。

图7 安装角对体积分数标准差的影响
3.2.4 安装角对湍动能和湍动能耗散率的影响 湍动能与湍流速度涨落方差成正比[19]。湍动能越大,湍流速度涨落方差越大,流场紊乱程度越高,两相混合效果越好;湍动能越大,涡流扩散速率越大,微观混合时间越短[20]。湍动能耗散率越大,电机所需的单位体积搅拌功率越大,各安装角度下水洗槽内不同截面的湍动能、湍动能耗散率云图如图8、图9所示。由图8、图9可知:各安装角下水洗槽内的湍动能和湍动能耗散率均从近潜水搅拌器处向远离潜水搅拌器处减弱;近潜水搅拌器上游处混合效果好于远离搅拌器的下游,而近潜水搅拌器上游处所需的单位体积搅拌功率要高于远离搅拌器的下游;α为20°时,高湍动能区所占面积最大,搅拌效果最佳;α为25°、30°、35°时,在潜水搅拌器Ⅰ下侧近壁面区域的湍动能相较其他区域要小,混合效果较差;α为20°时的湍动能耗散率高于其他安装角度的,说明α为20°时所需的单位体积搅拌功率较大;α为40°时,湍动能耗散率较小,说明此处所需的单位体积搅拌功率较小。考虑到湍动能耗散率,安装角为40°时较佳。

α=0° α=5° α=10°

α=15° α=20° α=25°

α=30° α=35° α=40°图8 不同安装角度时水洗槽湍动能云图
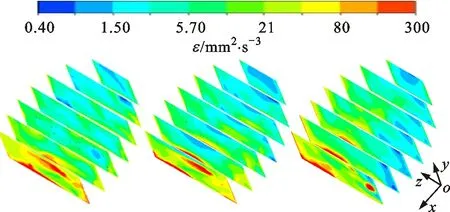
α=0° α=5° α=10°

α=15° α=20° α=25°

α=30° α=35° α=40°图9 不同安装角度时湍动能耗散率云图
4 数值模拟计算法有效性的验证

(a)α=20°

(b)α=40°图10 两潜水搅拌器扭矩模拟值与实验值比较
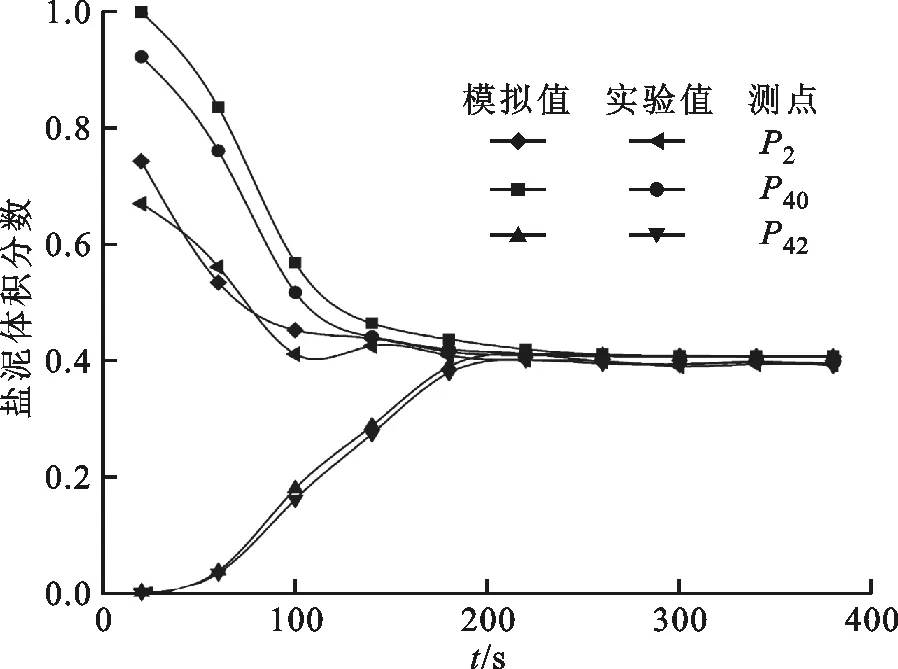
(a)α=20°

(b)α=40°图11 盐泥体积分数模拟值与实验值比较
为验证数值模拟分析的合理性,本文选取α为20°、40°的水洗设备进行搅拌实验,并将测得的两个潜水搅拌器实际扭矩值和检测点盐泥体积分数分别与数值模拟结果进行对比分析。实验所用盐泥取自国内某盐业公司,水洗设备是本课题组为某盐业公司制作并已投入运行的机型,其潜水搅拌器叶轮直径、额定转速均与数值模拟时采用数值一致,即两潜水搅拌器叶轮直径为620 mm,转速为480 r/min,扭矩的测量采用电测法,电阻应变片紧贴于搅拌轴应变元件上,从扭矩测试仪中读取实际扭矩值。测量盐泥体积分数的过程是利用取样器在P2、P40和P42点实时采样,将定容盐泥样品进行真空抽滤后用烘烤箱烘干得到盐泥颗粒,再利用排沙法测量盐泥颗粒的体积,并与盐泥样品体积相除计算出检测点的实际盐泥颗粒体积分数。将实验和数值模拟计算得到的扭矩数据和检测点处盐泥体积分数绘制曲线,如图10、图11所示。由图10、图11可知,α为20°、40°时潜水搅拌器Ⅰ和潜水搅拌器的扭矩均随搅拌时间上升后趋于平稳,潜水搅拌器Ⅱ的扭矩随搅拌时间下降后趋于平稳,且潜水搅拌器Ⅱ的扭矩始终大于潜水搅拌器Ⅰ的扭矩。监测点P40、P2的盐泥体积分数随搅拌时间下降后趋于平稳,P42的盐泥体积分数随搅拌时间上升后趋于平稳。实验和数值模拟的扭矩曲线和各检测点盐泥体积分数曲线基本吻合,产生误差的主要原因是由于数值模拟未考虑泵送水洗剂对盐泥的扰动,物料混合时的温度变化以及实验存在测量误差的影响。实验值与模拟值的误差在12.3%以内,数值模拟结果基本可信。
5 结 论
本文提出了一种盐泥专用水洗设备,即双潜水搅拌式水洗设备,借助Fluent 17.0软件选用多重参考坐标系法(MRF)对潜水搅拌器的混合过程进行了两相流场的模拟仿真,对比分析了两潜水搅拌器以不同安装角度时该水洗设备内的流速场与混合特性规律,得出如下结论。
(1)各安装角度下的搅拌流场不具对称性,近潜水搅拌器区域中高流速区占比较大,流动较为紊乱,且高速区多集中在罐体近壁面处,低流速区集中出现在远离搅拌器的中游处;α为20°时,整个流体域内低流速区占比小,远离搅拌器的下游处流速较高且分布均匀,利于水洗剂和盐泥的混合。
(2)水洗搅拌过程的混合特性受搅拌器安装角度影响显著。当α为20°时,混合时间和混合时间数均最小,混合均匀度最佳,适用于快速式搅拌模式;而当α增大至40°时,湍动能耗散率最小,单位体积混合能最小,可达到最佳的节能效果,适用于持久式搅拌模式。

