基于回弹补偿法的板材成形加工

褚式新, 茅云生, 郭 荣, 陶 韬

(武汉理工大学 交通学院， 湖北 武汉 430063)

0 引 言

近年来，由于船舶精度制造概念的普及，工厂对于板材的成形精度也提出了更高的要求。20世纪五六十年代起源的水火弯板技术[1]由于对工作人员的经验有很高的要求以及其艰苦的操作环境等特点已无法满足现代化生产模式，逐渐被机械冷弯加工所替代[2]。越来越多的学者聚焦于板材的冷弯加工：王呈方等[3]提出一种应用于船体外板三维曲面成形加工的新方法——方形压头可调活络模具板材曲面成形方法，冷弯成形虽可提高板材成形速度，但在成形精度上受回弹影响较大，回弹问题是冷弯成形普及的阻碍；GARDINER[4]在理想弹塑性材料前提下推导回弹前后曲率半径的表达式；HUANG等[5]通过板材的空弯试验验证Gardiner回弹预测公式的准确性，曲率半径的表达式不能直接指导板材的成形加工，需转换成其他物理量来指导具体加工；茅云生等[6]基于三辊弯板机研究上辊下压量与板材成形半径关系呈幂指数数学模型，消除回弹影响的方法通常采用补偿法；ORAL等[7]和余同希等[8]讨论了柱形弯曲回弹的模具补偿算法；王晓林等[9]对非圆弧弯曲回弹的模具补偿算法进行研究。利用回弹预测结果指导具体板材成形加工的文献较少。本文通过补偿的概念，利用回弹预测公式，结合实时曲率测量，引入具体物理量指导板材成形加工，达到板材成形加工速度与精度的结合。

1 回弹预测公式

1.1 基本假设

板材的冷弯成形加工与回弹有关，为了消除回弹对精度的影响，必须对其进行研究。GARDINER等在研究回弹时，通过假设忽略一些次要因素，最后得到的简单无因次公式为

(1)

式中：Rb为回弹前的板材曲率半径；Ra为回弹后的板材曲率半径；σs为材料屈服应力；E为材料弹性模量；t为板厚。

Gardiner解析公式是在一系列假设下推导出来的，为了获得公式的适用范围，必须知道推导时忽略了哪些次要因素。假设如下：

(1) 单轴应力假设。横截面上任意一点只能被单向拉伸或压缩。

(2) 横截面假设。变形前为平面的横截面弯曲变形后依然保持平面，并垂直于轴线。

(3) 理想弹塑性假设。应力分布式为

(2)

式中：σ为横截面任意纤维层的应力；ε为对应的应变；εs为弹性极限应变。综上，Gardiner公式可应用于窄板纯弯曲作用下的成形加工。

1.2 试验验证

为说明经典回弹公式对回弹预测的精确度，选取文献[10]中的空弯试验装置和试验数据对其进行验证。试验平面模型图如图1所示。

图1 空弯试验平面模型

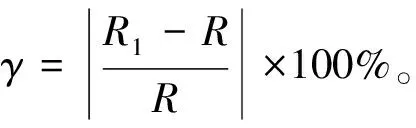
由表1可知：Gardiner公式的预测精确度高，在5种材料、20组试验下，最大误差为2.649%。可认为Gardiner公式可使用于目前工厂加工的大部分金属板材的冷弯回弹预测上。

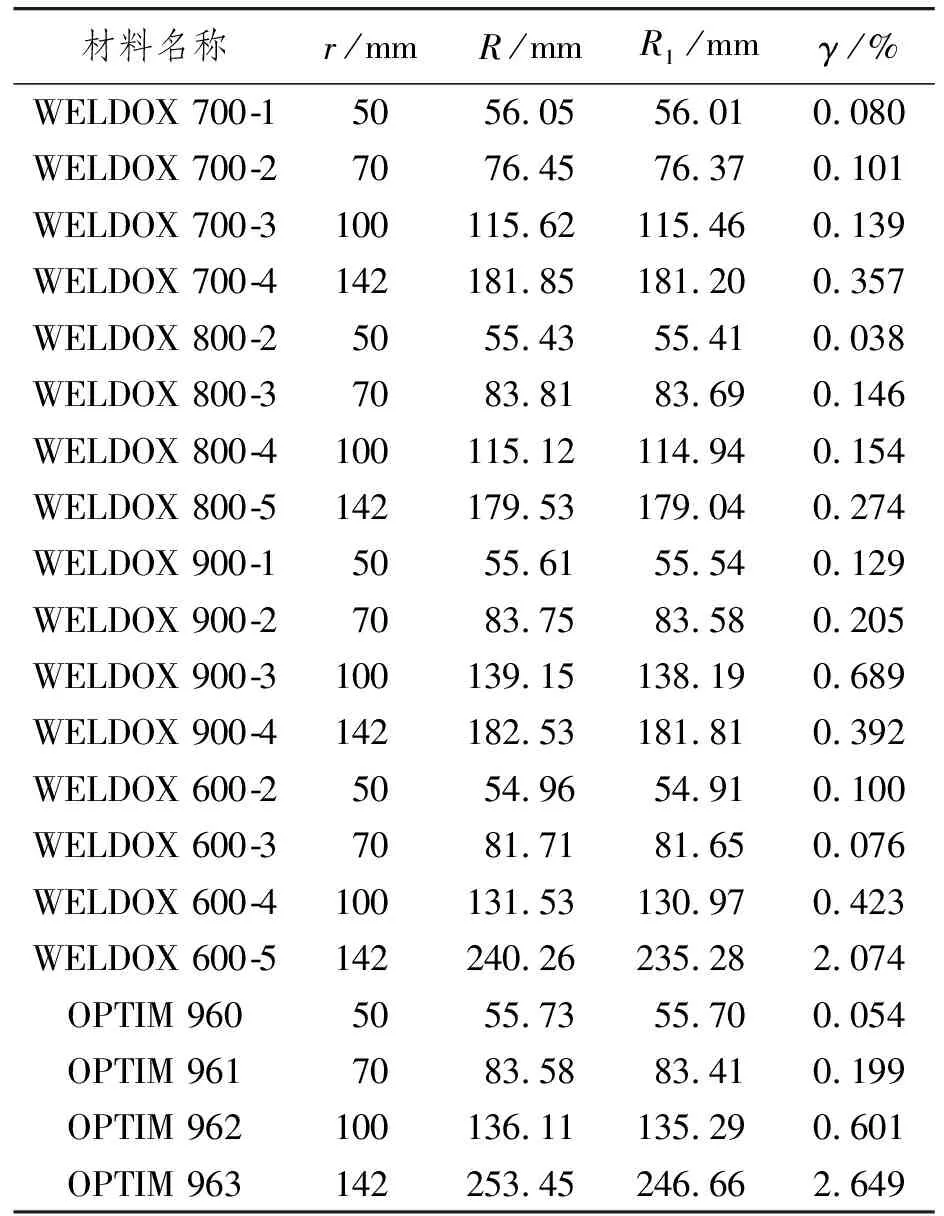
表1 Gardiner公式回弹预测值与真实值的对比

2 补偿法

2.1 补偿法概念

板材在加工成形中受回弹影响难以得到精确的加工结果，在工程实际中往往采用补偿的形式减小或消除回弹带来影响。补偿法是指在板材成形加工中利用过弯的形式消除由回弹带来的精度问题的影响。目前学者都是从其加工半径来表述回弹现象，难以实际应用到加工过程中，必须结合曲率测量装置才能明确指导加工。本文设置一种新型的曲率测量装置，结合Gardiner回弹预测公式以指导板材成形加工。

2.2 补偿法的实际补偿物理量

板材在油压机上进行单曲率弯曲成形可看作3点弯曲，由于加工段相对于整个板材的长度而言较小，因此加工段可近似用圆弧代替，未加工段保持直线。整个加工图如图2所示：A点为长度传感器设置点；与模具右端相隔距离为a；两模具相隔距离为b；模具高度为c；B点为板材直线部分延长线与模具中心线的交点；O点为加工板材弯曲圆心；β为板材直线部分与水平线的夹角；θ为加工弯曲段板材圆心角的一半；L1为此时刻A点设置长度传感器的值；t为板厚。

图2 曲率半径测量平面示例

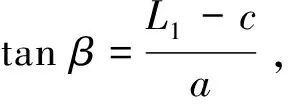
r=f(L1,a,b,c,t)

(3)

根据长度传感器A实时测量得到板下边缘高度，根据式(3)可得板的瞬时曲率半径，实现板材加工过程中的曲率半径实时测量。

补偿法是通过设计的曲率测量装置将曲率半径表达为某处传感器测量的板材下边缘高度相关的数学表达式，用补偿高度的形式补偿板材加工的曲率半径。

3 板材加工成形

根据第2.2节介绍可知：可通过实时测量板材下边缘的高度计算板材实时曲率半径，可采用补偿高度的方式实现在加工过程中用回弹预测公式指导板材成形加工。具体指导操作如图3所示：状态2是实际加工所需曲率半径；状态1是加工到状态2后经过回弹后板材实际状态；状态3是经过补偿法后加工回弹前状态，回弹后得到理想状态2。其他量如第2.2节所述。

图3 实际加工指导图

如想知道状态3的实际位置，需知L3的大小。表1的实际数据验证了Gardiner公式的精确性以及适用范围，可以用其指导加工。首先进行第一次加工，加工到位置2，传感器A测得距离为L2,卸载后让其回弹到状态1，此时传感器A测量得到此状态下板材下边缘的高度为L1。将数据代入式(3)，得到这两种状态下的曲率半径，记为：r2=f(L2,a,b,c,t),其为状态2对应的中性层半径；r1=f(L1,a,b,c,t)，其为状态1对应的中性层半径。由于目前工厂加工材料的多样性，包括各类合金，不可能将每一种材料都进行拉伸试验得到材料的属性参数，这样成本高且耗时。本文根据Gardiner公式的普遍使用性和其超高的精确度，可反推算出加工材料的属性参数。

(4)

将r2=Rb、r1=Ra代入其中，可解得εs=f(L1,L2,a,b,c,t)。

第二次加工时将板材加工到状态3，使其回弹至状态2，状态3的具体位置需根据传感器测量得到的板材下边缘高度决定，L3为状态3下传感器A的读数。将r2=Ra、r3=Rb代入式(4)中，与弹性极限应变表达式εs=f(L1,L2,a,b,c,t)联立，解得

L3=f(L1,L2,a,b,c,t)(5)

即在加工过程中，当传感器A显示距离为f(L1,L2,a,b,c,t)时，可停止加工，即可得到精确加工成形的板材。

4 结 论

对Gardiner回弹预测公式进行分析和试验数据验证，分析板材实际加工过程，得出如下结论：

(1) Gardiner回弹预测公式的精确度高，可用于目前工厂加工的大部分金属板材的纯弯曲回弹预测。

(2) 板材的曲率半径可通过一种新型实时曲率测量装置转换为另一物理量——某处板材下边缘的高度来表示，实现曲率半径的实时测量。

(3) 利用回弹预测公式的普遍适用性，可反推材料的属性参数，减少工厂为材料的参数而做拉伸压缩试验，亦可缩短加工周期。

(4) 根据一系列分析和计算，得到补偿量的具体表达式，可应用于板材的成型加工，提高板材加工速度和精度。