大尺寸薄板翻身非线性有限元结构响应

林文平， 何 远， 陈 红， 梁 君

(青岛北海船舶重工有限责任公司 船舶与海洋工程设计研究所， 山东 青岛 266520)

0 引 言

随着造船效率及平板焊接精度的不断提高，大尺寸拼板出现了多种施工方案。船厂常规的钢板拼接是通过单面焊双面成型的方法，避免了钢板翻身，但这种工艺导致的问题是钢板焊接完成后变形较大，不利于钢板平整度控制。

随着对制造精度的要求越来越高，在采用单面焊接后，翻身进行另一面焊接的工艺在青岛北海船舶重工有限责任公司船舶与海洋工程产品上得到应用[1]。图1为某尺寸薄板吊装翻身示例。

图1 薄膜板吊装翻身示例

起吊状态和竖直状态均是小变形问题，但随着起吊高度的不断增加，拼板中间的弯曲半径也不断增加，薄板的中间弯曲可达90°，不再是小变形问题。通过小变形线性力学理论解决该类问题的传统方法通常是设置大型工装以提高刚度，而利用大变形的非线性有限元方法解决该类问题不仅可节省工装成本，还可提高工程作业效率。

1 薄板定义

薄板尺寸大、厚度小，当满足以下条件时即为薄膜板：

薄板抗弯扭能力很低，抗弯刚度约等于零，横向外载荷由轴向力和中面剪力承担[2]。

2 非线性有限元基本原理

薄板翻身时位移较大，平衡方程和几何关系都是非线性的，属于几何非线性问题。另外，薄板与胎架的接触约束属于边界条件非线性问题。

2.1 几何非线性有限元分析

多维Green-Lagrange应变梯度表达式为

(2)

式中:Ekl为应变梯度；ul、uk为变形后的位移；xl、xk为变形前的位移。

Green-Lagrange 应变表达式包含变形梯度二次项。在小变形情况下，忽略位移的二次项对结果影响不大；在大位移、大应变情况下，必须采用几何非线性的Green-Lagrange 应变[3]。在大变形情况下，除了在应变表达式中包含几何非线性项外，力的平衡方程也应建立在变形后的物体构型上。当前变形状态下的应力为柯西应力σij，代表结构处于当前变形时的真实应力[4]。

用Lagrange方法描述有限元网格附着在物体上，随物体在空间中运动，建立某个质点的应力-应变关系。以当前变形构型为参考坐标系的更新Lagrange描述，在曲率项中直接引入几何非线性，采用柯西应力或真实应力、真实应变作为应力和应变的度量，可更好地表达大变形下的应力问题。

2.2 边界条件非线性有限元分析

接触问题是边界条件高度非线性的复杂问题，需准确跟踪接触发生前多个物体的运动，追踪接触发生后这些物体之间的相互作用，包括正确模拟接触面之间的摩擦行为。

产生接触的物体须满足无穿透约束条件：ΔuA·n≤D。式中：ΔuA为A点增量位移向量；n为单位法向量；D为接触距离容限[5]。

在数学上，施加无穿透接触约束方法有拉格朗日乘子法、罚函数法和直接约束法。

在该问题上，边界条件的非线性准确表达也是项目成功的关键因素之一。因此，必须充分关注边界条件的非线性。

3 翻身吊运工程实例

3.1 简要情况

图2为几块钢板焊接拼成22.1 m×18.6 m的大尺寸薄板，平放在胎架上。吊点安装在18.6 m侧边(图2中标示圆圈的边)，绕18.6 m侧边进行翻身，翻身高度至少为22.1 m。

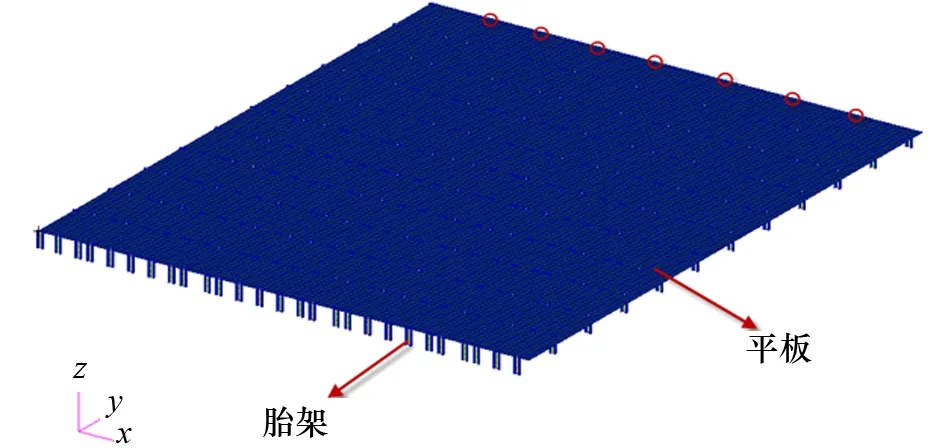
图2 钢板平放在胎架上示例

如图3所示，该大尺寸薄板由35 mm、25 mm与20 mm厚度的钢板拼接而成，两板之间由于只焊接了一面(另一面待翻身后焊接)，焊缝处板厚考虑为母材厚度的一半。

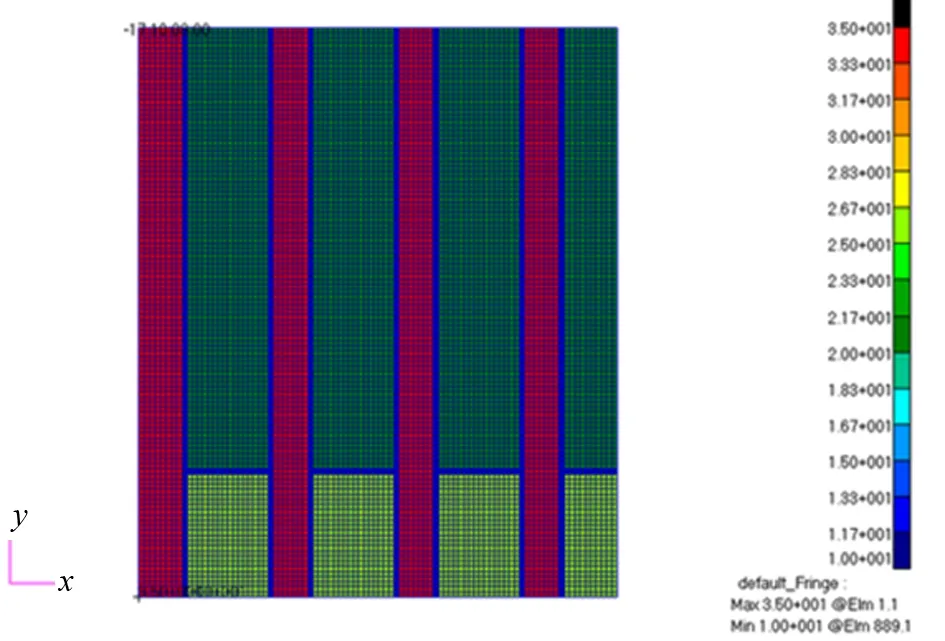
图3 板厚分布图

3.2 边界条件

假定薄板放置在胎架上，与胎架完全接触，胎架下端刚性固定在地面上。薄板与胎架的摩擦因数为0.15，在重力(g=9.81 m/s2)作用下，薄板一侧边沿竖直方向从0 m吊升至22.1 m，以实现平板翻身。

3.3 柯西应力计算结果及分析

如图4所示:在提升0～5.01 m阶段，薄板的弯曲半径随着提升高度的不断增加而增大，表征大变形下的结构响应参数——柯西等效应力随提升高度的增加而增大；在提升7.57 ～14.80 m阶段，薄板的弯曲半径不随高度的增加而增大，柯西等效应力亦保持稳定；在着地端不断减小的同时，薄板的弯曲半径亦不断减小，柯西等效应力也随提升高度的增加而不断减小。

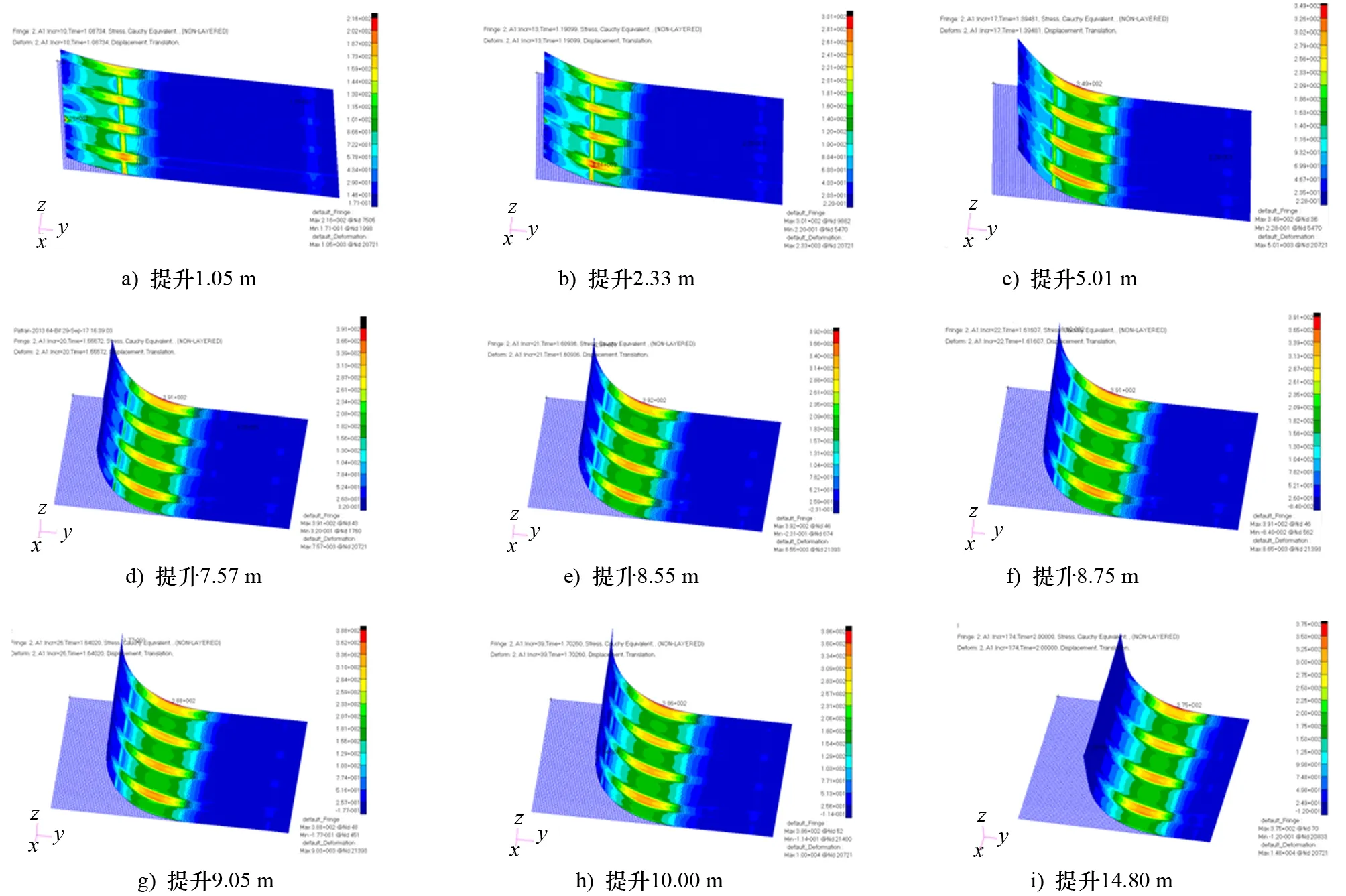
图4 柯西应力计算结果

3.4 吊点运动轨迹

如图5所示：在初始阶段，吊点上升速率大于前进速率；在达到稳定状态后，上升速率约等于前进速率；在后期，上升速率小于前进速率。

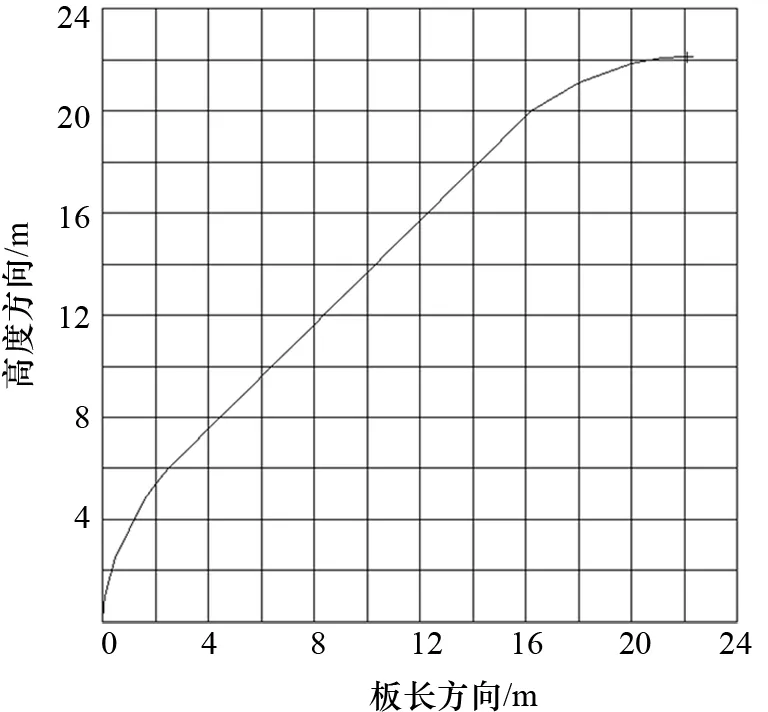
图5 吊点轨迹线

4 应力影响因素

4.1 薄板长度对柯西应力的影响

以30 m×12 m×10 mm薄板为例，柯西应力计算结果如图6所示。

图6 柯西应力计算结果

从图6可知：提升4.10 m后，应力响应值随着提升高度的增加而趋于恒定；在提升4.10 m前，应力响应值随着提升高度的增加而增加。可见：(1)当薄板长度大于弯曲半径影响范围时，结构最大应力响应值恒定；(2) 当薄板长度小于弯曲半径影响范围时，结构最大应力随提升高度增加而增大。

4.2 薄板宽度对柯西应力的影响

从图6的应力分布图可以看出，自由边对最大应力值有影响，但影响范围有限，故薄板宽度对结构最大应力响应值基本无影响。

4.3 支撑接触面几何形状对应力的影响

为了考察支撑接触面对应力的影响，对放置在刚性平面(摩擦因数考虑为0.15)上和2.00 m×0.77 m的槽钢胎架(摩擦因数考虑为0.15)上的薄板分别进行考察。

如图7和图8所示，与放置在刚性平面上的应力371 MPa相比，放置在2.00 m×0.77 m的槽钢胎架上的应力约增加18 MPa(389 MPa)。胎架间隙对局部结构产生了附加弯矩，导致最大应力响应值不同。因此，支撑接触面对应力值有影响，在实际应用中应予以考虑。

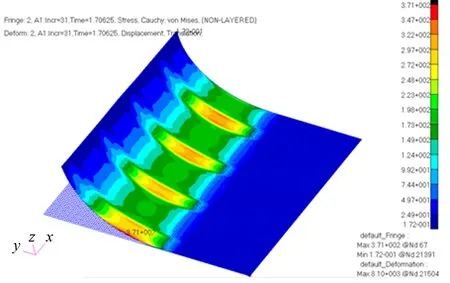
图7 放置在刚性平面上

图8 放置在2.00 m×0.77 m的槽钢胎架上

4.4 吊绳角度对应力的影响

从是否能产生附加弯矩的角度出发，当吊绳不是竖直起吊时：如吊车末端位于吊点的上前方，势必对弯板区域产生附加弯矩，造成应力增大；如吊车末端位于吊点的上后方，会减小弯板区域的弯矩，起到有利作用。图9为吊绳竖直起吊的应力响应结果，最大应力为371 MPa；图10为吊绳在上后方时的应力结果，最大应力为350 MPa。

4.5 支撑接触面摩擦系数对应力的影响

支撑面与钢板间摩擦系数大，对起吊前期应力有改善作用，但随着起吊高度的增加，最大弯曲应力趋于恒定。

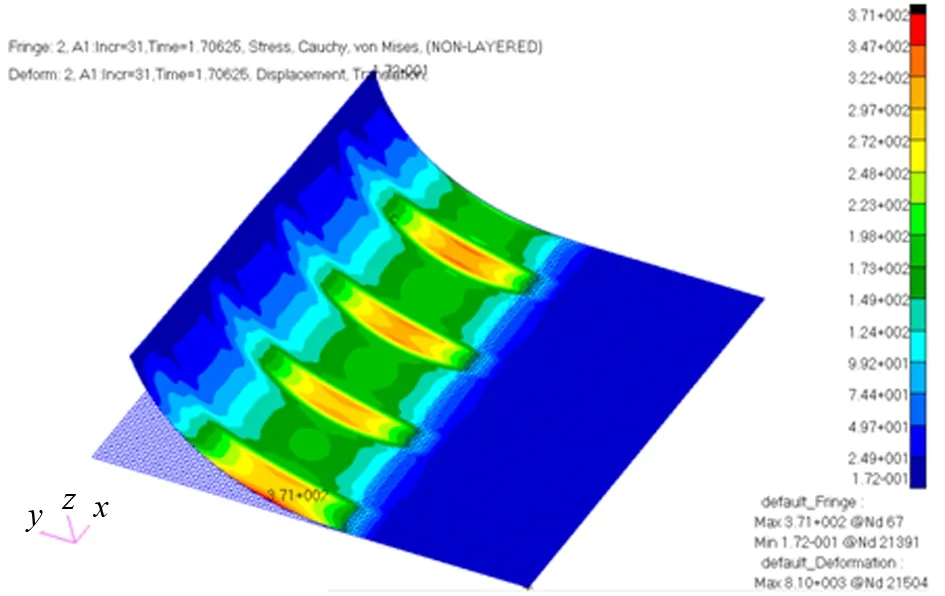
图9 竖直起吊计算结果

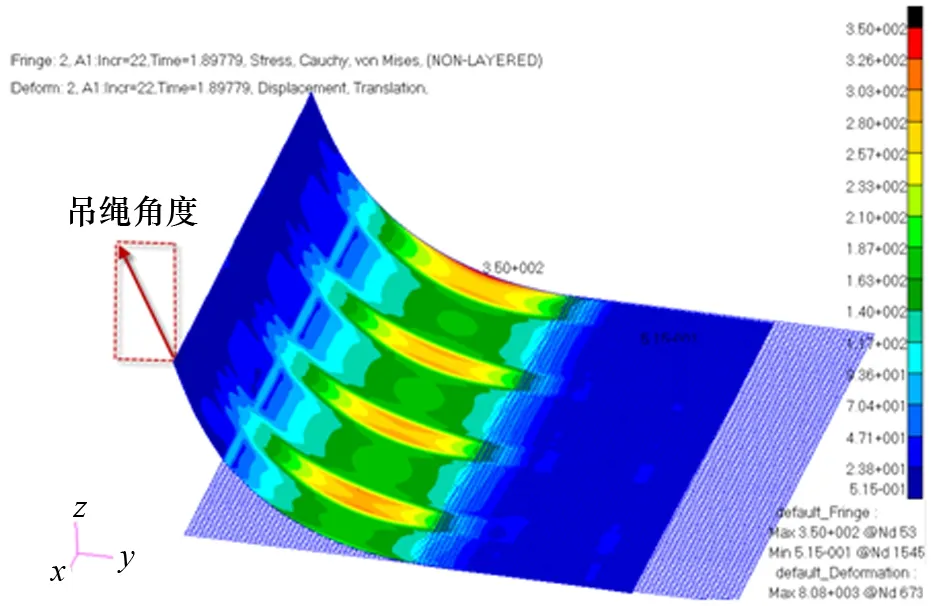
图10 带角度起吊(上后方)的计算结果

5 工程实际常见板厚的柯西应力结果统计

船厂薄板拼板后的最大长度不会超过30 m，以吊点竖直提升30 m×12 m×t(t为钢板厚度)放置于刚性平面上，薄板与刚性平面的摩擦因数考虑为0.15，对7～45 mm板厚的应力进行计算，结果如表1所示。

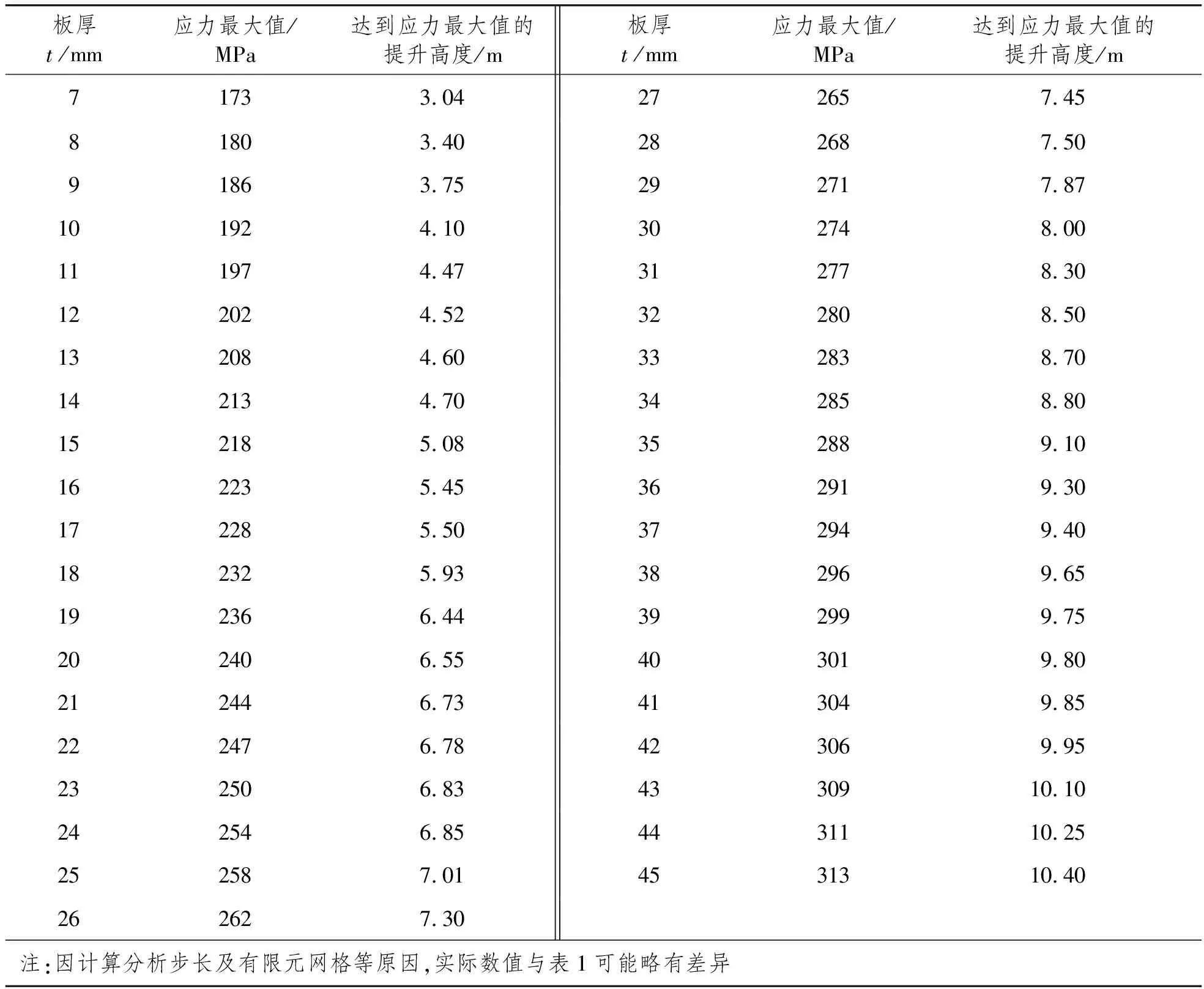
表1 常见板厚的应力计算结果

6 结 论

本吊运方案在第3节基础上考虑了第4节影响应力的几种因素，在青岛北海船舶重工有限责任公司的工程实践中取得成功。图11为薄板吊运过程中的图片。

图11 吊运过程

结合计算结果和工程实践得出以下结论：

(1) 当薄板长度较短时，弯曲未能达到最大值，其过程类似“似梁运动”，应力随提升高度的增加而增大。

(2) 当薄板长度较长时，弯曲达到最大值的同时，应力也达到最大值且保持恒定，直至弯曲开始逐渐减小时，最大应力也随之减小。宽度对最大应力影响不大，底部接触面的几何形状及摩擦力对最大应力有影响。

(3) 在薄板翻身前只焊透一半时，应考虑焊缝处板厚偏小给应力带来的影响。一般沿焊缝长度方向翻身的应力水平小于沿焊缝宽度方向翻身的应力水平。

(4) 表1计算所得的应力值未考虑环境因素，如大风、惯性力等影响，在实际工程应用中应加以考虑。