高阶中立型差分方程解的非振动性

张思逸

(湖南幼儿师范高等专科学校,湖南 常德 415500)

0 引言

高阶中立型差分方程振动与非振动理论在近几十年来得到了广泛的关注, 这是因为这种方程与微分方程的某些类似的现象非常接近. 此外，这些方程在物理学和其他领域有许多应用[1,2], 特别是, 包含有中立型与延迟项的方程在自然科学和技术中有着大量的应用[3-7]. 近些年来, 高阶中立型差分方程关于解的非振动性问题的研究受到很多关注, 基于上述已知的事实, 本文探讨了下面一类非线性高阶中立型差分方程

Δm{rnΔkxn}+f(n,xn)=gn,n≥n0,k=1,2,3,….

(1)

的解的非振动性. 其中n0,n∈Z+,rn,gn∈R,f(·) 是非负非减函数, 且Δ是一阶差分算子,即Δxn=xn+1-xn.Δm为m阶差分算子,其中m≥2且m∈N+, 定义为Δmxn=Δ(Δm-1xn).

1 预备知识及主要定理

定义2.1[2]如果存在正整数N, 对任意的n≥N,方程(1.1)都有解xn≥0，那么称{xn}是方程的最终正解; 反之称为最终负解.

定义2.2[2]如果方程(1)或者方程(1)的解{xn}既不是最终正解也不是最终负解，则称之为振动的；否则称之为非振动的.

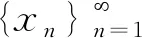
|xi-xj|<ε.

定理2.4[2](Schauder不动点定理)设X是Banach空间, Ω是X非空有界的凸闭子集. 如果有算子T:Ω→Ω是连续的且使得T(Ω)⊆Ω且T(Ω)是相对紧集.则T至少存在着一个不动点.

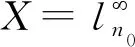
下面证明此文的主要结果.

定理2.5假设函数f是连续有界函数, 若存在n0∈N使得下列条件成立:

(2)

则式(1)存在着一个非振动解.

证明:现设M1,M2是正常数, 且有下面的条件成立:

M1≤α≤2α≤M2

设有集合

A={xn∈X:M1≤xn≤M2,n≥n1},其中n1∈N.

显然, A是集合X中的一个有界凸闭子集.

定义算子:

由假设条件可知存在着n0∈N, 使得当n≥n0时,有下式成立:

(3)

首先证明, 对n≥n1和xn∈A有S:A→A. 根据假设(2), 则有

另一方面, 由式(2)则有

因此就得到了S(A)⊆A，同时也证明了S(A)是一致有界集合. 下面证明映像S具有连续性.

取A中的数列{xnl},且当l→∞ 时有xnl→xn, 则

因为f是连续的, 即当l→∞ 时, 有 |f(j,xjl)-f(j,xj)|→0. 即有

这也就证明了S是连续的.

对任意的x∈A,N2>N1≥n1有

因此,|SxN2-SxN1|≤ε,综上所述, 根据定义2.3,则集合S(A)是相对紧集.再由定理2.4,则存在xnp∈A,使得Sxnp=xnp,p∈N.又由于 X 是一个完备的Banach 空间, 因此当p→∞ 时有xnp→x,即x是(1)的非振动解. 证毕.

类似地, 若设M3,M4是负常数, 且存在负常数α有下面的条件成立:M3≤α.再设X中的一个有界凸闭子集为B={xn∈X:M4≤xn≤M3}, 其中n1∈N且n≥n1.

定理2.6假设函数f是连续有界函数,若存在n0∈N使得式(2)成立. 则问题(1)在 B 上存在着一个非振动解.

证明:若n1∈N且n1>n0, 定义算子:

由假设条件可知当n1充分大时,存在正常数M使得 2α≤-M≤α且有下式成立:

(4)

首先证明, 对n≥n1和xn∈B有S:B→B. 根据假设(2.1), 则有

另一方面, 由式(4)则有

因此就得到了S(A)⊆A，同时也证明了S(A)是一致有界集合. 类似于定理2.5的余下的证明, 可以得到 S 是一个全连续算子. 因此根据定理2.4,则存在xnp∈A,使得Sxnp=xnp,p∈N.又由于 X 是一个完备的Banach 空间, 因此当p→∞ 时有xnp→x,即x是(1)的非振动解. 证毕.