车门框密封条断面结构的多目标优化＊

胡强 陈宇强 陈梓铭 李落星 吴岸

（1.湖南科技大学 难加工材料高效精密加工湖南省重点实验室，湘潭 411201；2.湖南大学 汽车车身先进设计制造国家重点实验室，长沙 410082；3.长安欧尚汽车研究院，重庆 400020）

主题词：车门密封胶条 泡状管结构 多目标优化

1 前言

车门框密封条作为汽车重要的密封部件，对汽车舒适性有重要影响。一方面，密封条压缩负荷的大小直接影响车门关闭时的轻便性和平顺性；另一方面，密封条与钣金件之间的接触宽度对整车的气密性及NVH性能起着重要作用[1-4]。目前，国内外对车门框密封条结构的分析及优化进行了广泛研究，提出了多种分析及优化方法。如，陈少伟等[5]将试验设计方法与遗传蚁群融合算法结合，获得了密封条材料参数，优化了密封条压缩负荷曲线；赵建才等[6-7]将遗传算法和神经网络相结合，得出密封条结构设计参数与压缩负荷、应力等的非线性全局映射关系；Cho JR等[8]运用基于密度法的拓扑优化方法对密封条的结构进行优化，使密封条的疲劳寿命得到了极大的提升。当前对车门框密封条结构优化的研究主要采用单一变量法，不能同时考虑密封条结构各参数的相互影响，也不能直接得到符合要求的密封条结构。

本文通过对某乘用车现有密封条结构的研究，提出了利用Isight多学科优化平台集成Sculptor、Abaqus、Meta软件的密封条泡状管结构多目标优化方法，该方法利用Sculptor建立的密封条泡状管参数化网格模型，以密封条的压缩负荷、接触宽度为优化目标，综合考虑密封条泡状管的壁厚、宽度两个参数的相互影响，直接得到符合要求的密封条结构。

2 密封条原始结构仿真分析及验证

2.1 密封条泡状管的非线性有限元分析

车门框整圈密封条的布局方式如图1所示。由于密封条长度方向的尺寸远大于其它方向的几何尺寸，可假定密封条所受外界载荷是平行于结构的横截面，同时在长度方向上均匀分布。因此，为提高仿真分析效率，将密封条的变形问题转化为二维平面应变问题进行分析[7-9]。

图1 汽车车门框密封条装配示意

根据密封条的几何模型，利用Abaqus软件建立密封条二维平面仿真模型，如图2所示。整个仿真模型采用四结点双线性平面应力、减缩积分、沙漏控制的“CPSR4”四边形单元，单元尺寸为0.2～0.3mm，单元总数为4 532个。为更好验证仿真模型的正确性、评价现有密封条结构的合理性，对有限元模型中的车门施加7mm的压缩位移，并输出压缩过程中的压缩负荷和接触宽度。

有限元仿真模型中海绵橡胶采用Foam模型，应变能密度函数为[10-11]：

式中，μn、αn、βn为材料常数；λ1、λ2、λ3为主伸长比。

密实橡胶采用Mooney-Rivlin模型，应变能密度函数为[11-13]：

式中，C10、C01为与温度有关的材料常数；D1为橡胶不可压缩参数；J为橡胶变形前与变形后的体积比；I1、I2为等容Cauchy-Green张量的第一、第二不变量。

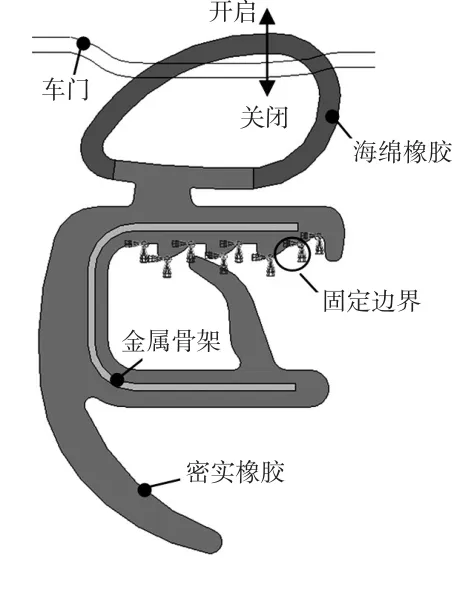
图2 密封条有限元仿真模型

根据整车设计要求，车门关闭后，在满足车门与车身之间均匀密封间隙前提下，需保证车门框密封条的压缩量为4±2mm，此区间内，长度100mm的密封条的压缩负荷、接触宽度的技术要求如表1所列。

表1 压缩量为2～6mm内的压缩负荷及接触宽度技术要求

2.2 仿真结果分析及验证

基于Abaqus软件对现有车门框密封条的压缩负荷和接触宽度进行了有限元仿真分析，同时利用CMT2005万能试验机和工装试验台对密封条进行压缩试验（图3），得到密封条实际的压缩负荷及接触宽度，并与仿真结果进行对比，结果如图4及表2所示。

图3 密封条压缩试验

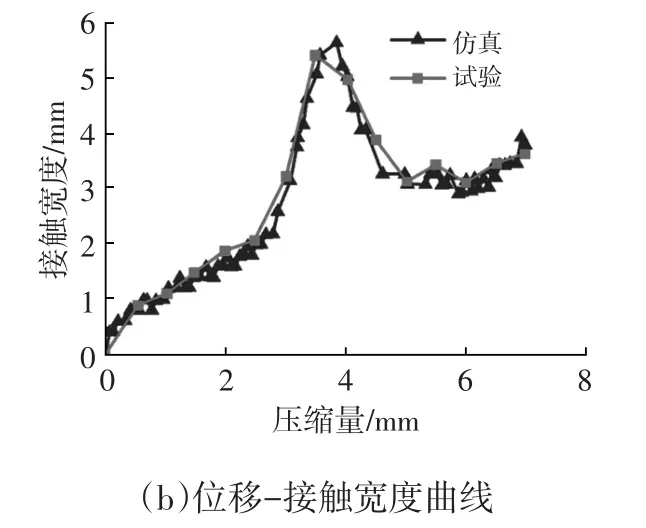
图4 密封条原始结构仿真及试验结果对比

表2 密封条原始结构的压缩负荷、接触宽度仿真值与试验结果对比

由图4和表2可知，仿真结果与试验结果有较高的一致性。压缩量在7mm内，压缩负荷及接触宽度的仿真与试验结果相对误差都在10%以内，符合仿真精度要求。因此，所建立的密封条仿真模型能很好地分析密封条在实际压缩过程中的受力、接触情况。同时，试验结果进一步证明原始密封条的压缩负荷、接触宽度都不满足技术要求，需对密封条泡状管的结构进行优化。

3 密封条泡状管结构优化

3.1 设计变量及优化目标的确定

密封条的压缩负荷、接触宽度主要与密封条泡状管的截面形状（壁厚、高度、宽度）、压缩量、材料特性及与金属薄板之间的摩擦特性等参数有关[14]。考虑密封条实际密封间隙和装配要求，密封条泡状管优化时不考虑其高度的变化。对于相同材料密封条，在压缩量i相同时，压缩负荷F、接触宽度L是壁厚t、宽度w的函数。因此，建立如式（4）的目标函数及约束条件，那么，密封条结构优化问题即转化为对参数t、w进行优化，可得出合理密封条泡状管结构。

3.2 密封条泡状管优化流程

采用基于均匀B样条技术的Sculptor软件，建立如图5所示的密封条泡状管参数化网格模型。

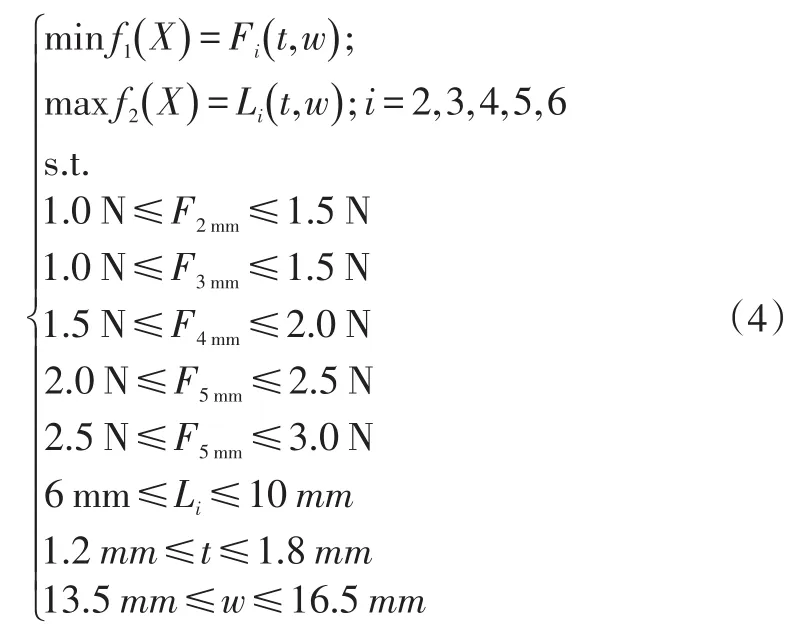
图5 密封条泡状管参数化网格模型

密封条泡状管结构优化流程如图6所示。将Sculptor参数化网格模型导入Abaqus软件中，对优化结构进行仿真分析，导出压缩负荷、接触宽度和应力等相关变量。通过Meta宏命令对输出变量进行解析。由Isight多学科优化平台进行试验方案设计及优化结果的判断。优化算法采用NSGA-Ⅱ算法[15]，优化设计中种群大小设置为12，遗传代数设置为20。

图6 密封条泡状管结构优化流程

3.3 密封条泡状管优化结果分析及验证

从初始方案开始，经过NSGA-Ⅱ优化算法寻优后，得到了满足要求的优化结果。利用Abaqus对优化后的密封条结构进行仿真分析，结果如表3所列。

由表3可知，优化后的泡状管在压缩量区间内的压缩负荷完全符合技术要求，在压缩量为2mm、3mm、4mm、5mm、6 mm时的压缩负荷为1.24 N、1.38 N、1.57 N、2.01 N、2.56 N，其仿真值与原始结构试验值相比，分别降低了17.33%、22.47%、34.31%、33.22%、40.47%，压缩负荷的波动量明显降低。

在压缩量为2～6mm内的接触宽度在2.72～6.33mm内变化。其中，压缩量为2mm和6mm时的接触宽度为2.72mm和3.91mm，不满足技术要求，但仿真值与原始结构试验值相比，其接触宽度分别增加了43.92%和24.92%，密封性能得到了较大提升。压缩量为3mm、4 mm、5mm时的接触宽度为6.07mm、6.33mm、6.14mm，均满足技术要求，仿真值与原始结构试验值相比，分别增加了92.70%、22.20%、94.92%。

表3 密封条泡状管结构优化后仿真值与原始结构试验值对比

对该优化方案进行了样件制造（图7），并对其进行压缩试验，结果见图8和表4。对比可知，优化后的密封条压缩负荷及接触宽度试验与仿真的相对误差都在12%以内，满足仿真精度要求，表明了优化结果的正确性及泡状管结构的合理性，同时也进一步说明了优化方法的可行性。

图7 优化前、后密封条结构对比

图8 优化前、后密封条泡状管的仿真及试验结果对比

表4 密封条泡状管结构优化前、后试验值对比

由表4可知，在压缩量为2～6mm内，密封条泡状管优化前、后的压缩负荷降低了20.22%～41.63%，接触宽度增加了27.03%～95.24%。

密封条泡状管设计时，除考虑其关门压缩过程中的压缩负荷及变形情况外，还需保证密封条在安装后，密封条泡状管在弯曲角度较大的情况下（车门及车门框的4个拐角处）不会发生起皱、下凹变形的情况[11-16]。为此，对密封条进行了实车安装，结果表明，原始结构的密封条泡状管在车门拐角的角度最大处有明显的下凹现象，如图9a所示，说明弯曲角度较大时，原始泡状管结构稳定性差，对密封条的使用寿命及车门关闭性能有较大的影响。优化后的密封条泡状管未出现起皱、下凹的情况（图9b），优化后的密封条泡状管的结构稳定性明显优于原始结构，可以用于生产及实车安装。

4 结束语

图9 优化前、后密封条泡状管结构稳定性对比

针对传统优化方法难以同时考虑多参数对密封条泡状管结构进行优化的问题，提出了利用Isight多学科优化平台集成Sculptor、Abaqus、Meta软件的密封条泡状管结构优化方案，试验结果表明：

a.该优化方案能综合考虑密封条泡状管壁厚及宽度两个参数，得到满足技术要求的密封条泡状管，从而有效地减小产品设计更改的次数，缩短设计周期。同时，试验结果验证了优化方法的可行性及优化后密封条泡状管结构的合理性。

b.相比于原始结构，优化后的密封条在压缩位移为2～6 mm内的压缩负荷较改进前降低了20.22%～41.63%。接触宽度相对优化前增加了27.03%～95.24%，既满足了密封性能，又有效改善了车门关门力及关门品质。