侗族风雨桥建筑艺术中的数学文化①
吴秀吉 罗永超
(1.贵州省凯里学院附属中学 556000; 2.贵州省凯里学院数学科学学院 556011)
风雨桥是侗族最具特色的建筑之一.她和侗族鼓楼、侗族大歌,被列为侗族“三宝”,闻名于世.她是侗族人民勤劳智慧的结晶,更是侗族艰苦创业、勤劳爱家的民族独特的人文景观.风雨桥已经不仅仅是实用意义上的桥,更是侗族人民追求现实完美、追求灵魂超越的象征.整个桥身不用一钉一铆以及其他铁件,皆以质地耐力的杉木凿榫衔接而成,集桥、廊、亭、塔、楼阁的建筑特色于一体.风雨桥是所有桥梁建筑中的明星,她是侗族桥梁建筑艺术的结晶.
风雨桥的主体结构对称和谐,其亭、塔平面图通常是正方形、正六边形和正八边形,但也有平面图一般由正方形和正八边形复合组成.其平面结构图(如图1所示)内部是一个正方形A2B2C2D2,而外部是一个与正方形A2B2C2D2同心的正八边形A2EB2FC2GD2H组成.古代侗族没有量角器,风雨桥建筑师仅凭一把直角刻度尺(风雨桥建筑师通常称为“角尺”,如图2所示,较短的直角边带有刻度)和一只竹笔(竹笺:如图3所示),在实践中总结出了很多几何作图的方法.尽管风雨桥建筑师门派较多,同一种图形的画法也不尽相同. 本文对侗族风雨桥建筑的整个工艺过程和制作流程中所包含的数学原理进行研究得出以下结果.
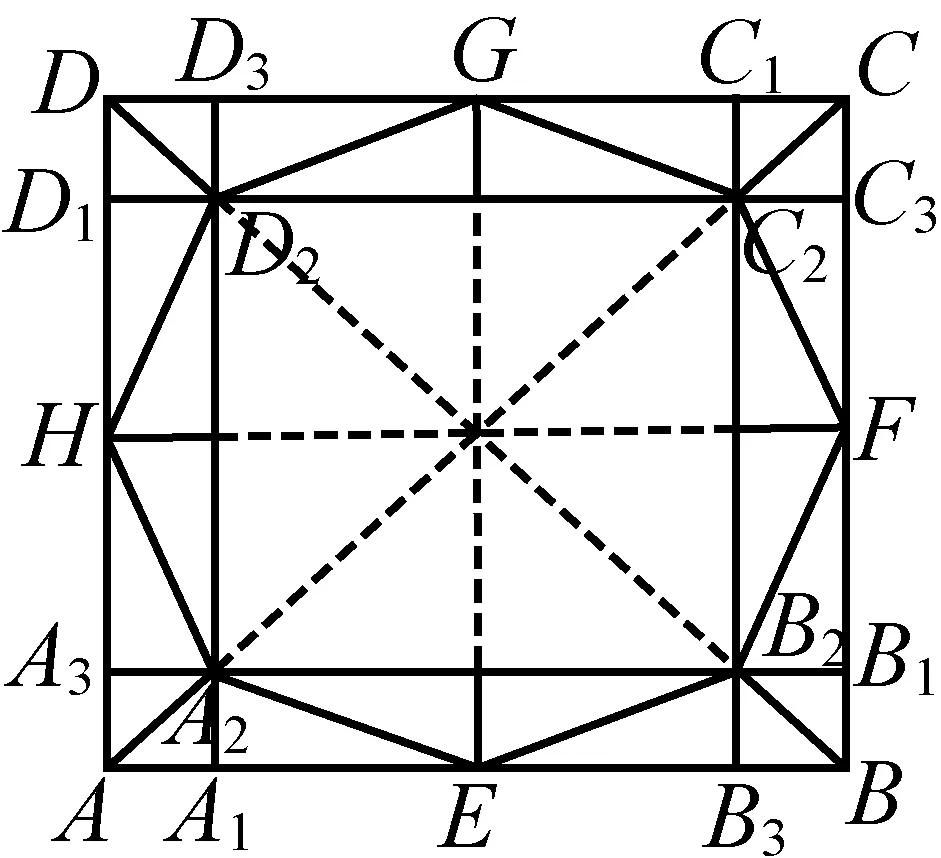
图1

图2 直角刻度尺

图3 鼓楼建筑师常用的竹笔
1 风雨桥建筑的初等几何
我们注意到,建造一座平面结构图为内部是一个正方形,而外部是一个与正方形同心的正八边形组成的风雨桥亭、塔,凿柱眼时需要做成135°和22.5°的角,他们通常是通过作等腰直角三角形底边上的中线平分直角去实现的,过程如下:
首先,在准备好的呈圆柱(实际上是不规则)的原木,(如图4)两头(横截面)分别吊垂线A1A2及A′1A′2,并用墨线分别连接A1A′1及A2A′2;然后将原木旋转90° ,重复前面的方法作出B1B2,B′1B′2,B1B′1,B2B′2, 且A1A2⊥B1B2, 垂足为O,A′1A′2⊥B′1B′2, 垂足为O′ ;这实际上是将原木抽象为直线OO′ 的过程(O及O′未必是原木两头横截面中心,横截面也未必是圆面).

图4
其次,分别在OB1,OA2(或O′B′1,O′A′2)上取A,B(或A′,B′),使得OA=OB(或O′A′=O′B′),连接AB(或A′B′),并找出AB(或A′B′)的中点C(或C′),连接OC(或OC′)其延长线与横截面的边缘交于R(或R′),用墨线连接RR′.
再次,分别在OR,OA1(或OR′,O′A′1)上取H,D(或H′,D′),使OH=OD(或O′H′=O′D′),连接HD(或H′D′),并找出HD(或H′D′)的中点F(或F′),连接OF(或O′F′),在HD(或H′D′)上取G,E(或G′,E′),使OF=FG=FE(或O′F′=F′G′=F′E′),连接OE,OG(或O′E′,O′G′)其延长线与横截面的边缘交于V,N(或V′,N′),用墨线分别连接VV′,NN′.
最后,在A1A′1,RR′,VV′,NN′上的任一指定位置M′,X,P,Q上沿直线OO′ 垂直相交的方向钻孔(凿柱眼),两孔(柱眼)XO″及M′O″ 所确定的方向成135°角,XO″及QO″和M′O″及PO″ 所确定的方向都成22.5°角,四根主承柱按同一方法完成后,用等长的木枋与柱连接起来得到正方形,另外四根副承柱制作过程和正八边形制作过程完全一致,再用等长的木枋把主承柱和副承柱连接起来即可得到内部是一个正方形,而外部是一个与正方形同心的正八边形.

图5
建造一个平面结构图为正六边形(如图5)的风雨桥亭、塔时,其方法与上面(图4)类似,但不同的是在原木的横截面上分别吊垂线A′D′及H′G′,且A′D′⊥H′G′垂足为O,在A′D′上取OB=OE,再分别取OB,OE的中点G,H,过G,H分别作A′D′的垂线F′B′,G′C′.取OA=OB交F′B′于A,过A,O作直线交C′E′于D.用同样的方法分别在F′B′,G′C′找到另外两点C,F,最后依次连接A,B,C,D,E,F就得到一个正六边形.
2 以风雨桥为载体的侗族数学文化
风雨桥是侗族桥梁建筑的明星,是侗族建筑文化艺术的结晶.它与侗族同胞平时的物质与精神生活密不可分.它也是记载着侗族千百年桥梁建筑历史文化的一本木建实物书.随着时间的推移,岁月的变迁,风雨桥亭、塔的造型也发生了相应的变化.如此精致的建筑,整体以杉木做柱,枋,凿榫衔接,横穿斜套,纵横交错,结构严谨且牢固,却不用一钉一铆,其中蕴涵着丰富的数学文化.
2.1 风雨桥建造技术中的比例关系
下方上八角攒尖亭、塔的建造,涉及到正方形的边长a与正八边形的边长b的计算.在今天可以用公式a=2bsin67.5° 表示.显然67.5° 不是特殊角,计算结果无疑是取其近似值.但古代侗族对角度的概念并不是十分清晰,对此,他们有自己的计算方法:

图6
图6是亭、塔正八边形和正方形在平面上的正射影,已知正方形的边长AB的长度,则边长AC和DC确定是通过公式:
AC∶AD∶DC=13∶12∶5
(1)

2.2 “二分法”在风雨桥建筑技术中的应用
建造六角亭、塔,需要制作正六边形.进一步调查发现与黔东南毗邻的三江县境内有部分建筑师傅用“二分法”去近似地6等分圆周,这是古代侗族对角度概念尚未完全掌握的历史条件下6等分圆周的近似方法.其具体过程如下:

图7
首先,在圆柱形(实际上是不规则的)木料底面(如图7)上作线段PQ及中点O,过O作A′B′⊥PQ垂足为O,取OA=OD.

最后,依次连接A,B,C,D,E,F就得到一个正六边形(如图7所示).就这样,实现了6“等分”圆周的目的,且每个角的误差都不超过15′18″.
2.3 风雨桥建造技术中的相关计算
图8是正六边形和正方形在平面上的正射影,建造下方上六角攒尖顶亭、塔(如图9),需要制作正六边形和正方形.在实地采访中得知建筑师傅在建造下方上六角攒尖顶亭、塔时,其正方形的边长有专门的计算公式:
正方形的边长=正六边形的半径×C(C为常数)
(2)
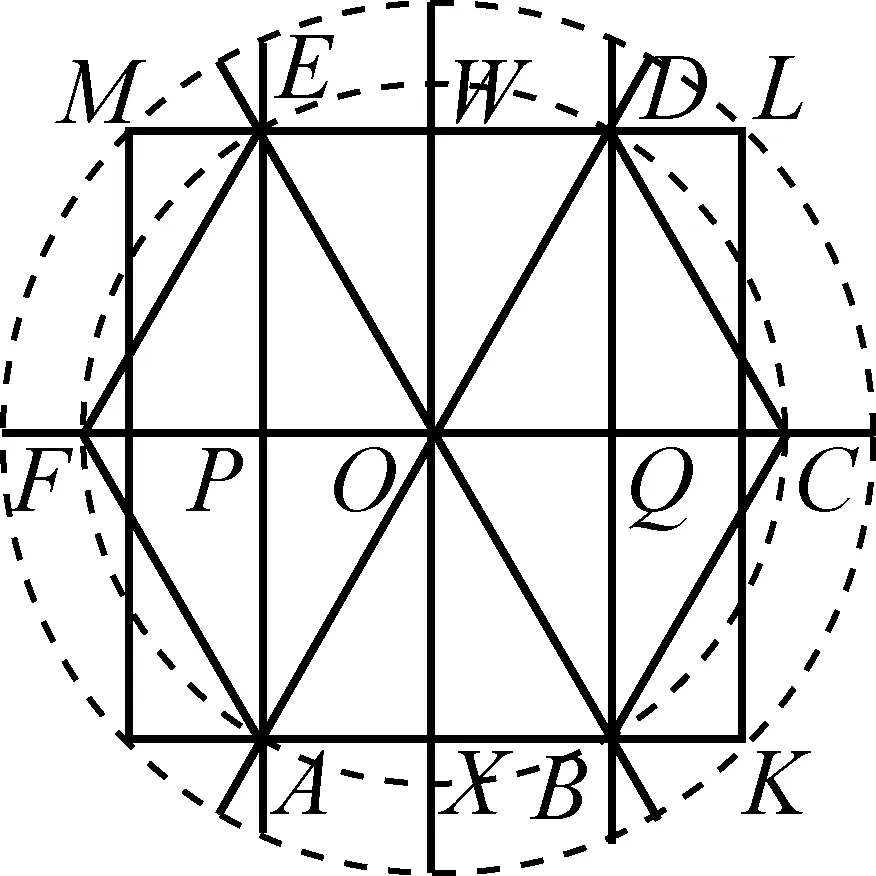
图8

图9
即图中的AE=AF×C(仅以AE,AF边为代表),建筑师傅从长期的实践经验中发现C=1.75较为合适.如果按现代数学中三角函数方法来求,则在Rt△OPE中∠EOP=60°,

从而有EP=OPtan∠EOP,


因此取C=1.75与理论值相差很小,又因为在实际测量过程中也存在误差,它显然是一个较好的近似计算公式.
2.4 风雨桥建筑结构中等差数列的运用
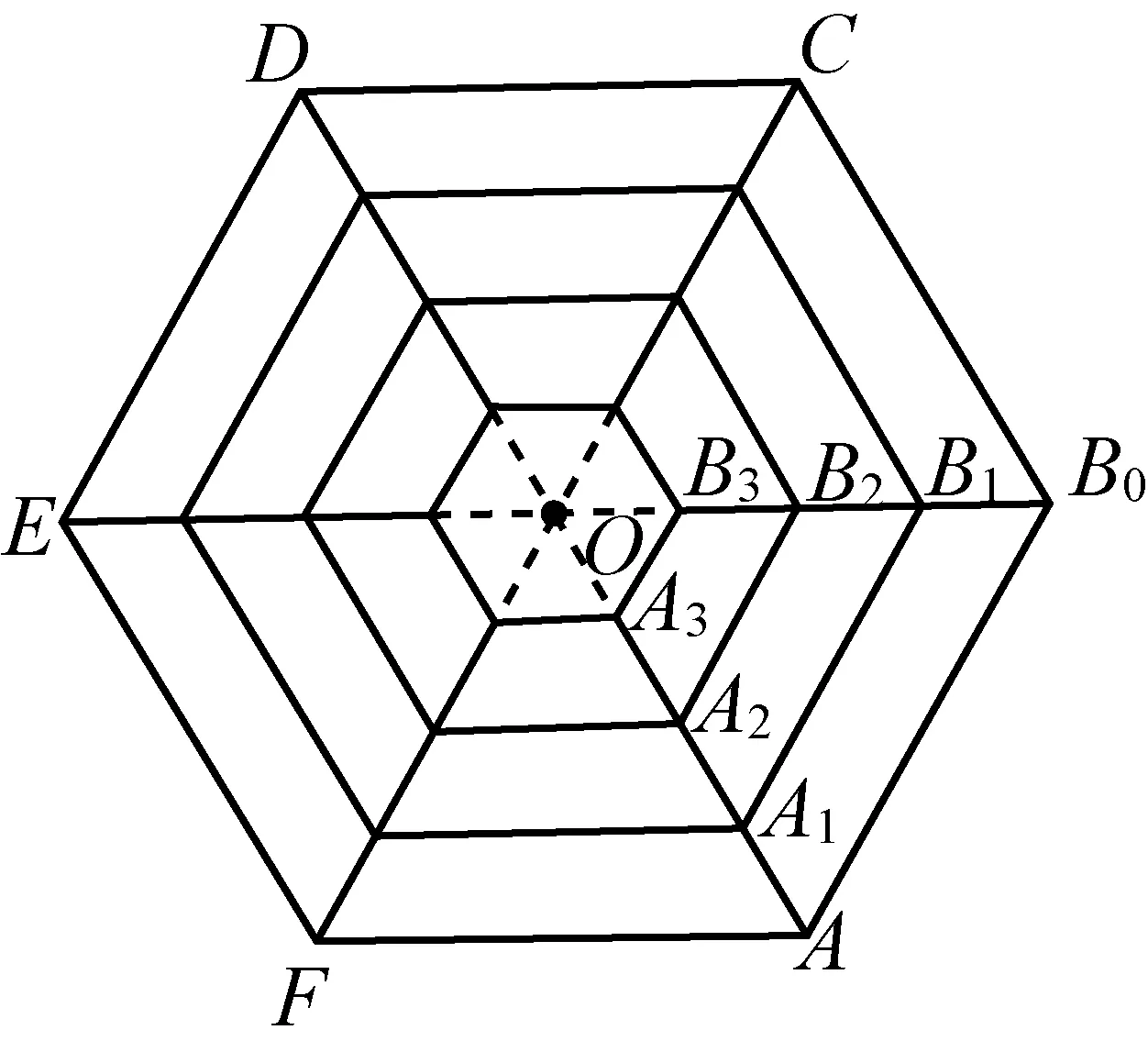
图10
图10是风雨桥中的亭、塔正六边形在平面上的正射影,在采访中得知建筑师傅在建造六角攒尖亭、塔时,其正六边形的边长自下而上成递减等差数列.其边长的计算方法如下:
A1B1=AB0-B0B1,A2B2=A1B1-B1B2,A3B3=A2B2-B2B3,…,AnBn=An-1Bn-1-Bn-1Bn,
其中Bn-1Bn=…=B2B3=B1B2=B0B1,n∈N+.不妨令a1=AB0,d=-B0B1.即就可以计算出第n个正六边形的边长为:
an=a1+(n-1)d,n∈N+
一般风雨桥亭、塔,自下而上每层翘檐递减,从而正六边形的边长和木枋的长构成一个递减等差数列.
综上所述,因为师傅建造风雨桥亭、塔的地基大小不同,不同大小亭、塔其所制作正六边形的边长也各不一样,建筑师傅通过这样的推算,从而确定需要多少材料,以免浪费.这说明侗族人民在建造风雨桥亭、塔时能够较好地利用“数列中按某一比例逐步增加或减少”的思想.
3 长度计算中的近似计算和单位的换算方法

图11
图11是风雨桥梁上的一个剖面图(即人形架).从图形上我们可以观察到
Rt△OB1A1∽Rt△OBiAi(i=1、2、3、4)两两相似,并且它们有一个公共角O.只要学过正切的人都知道:AiBi=OBi·tan∠O.其中OBi的长度为已知.而侗族没有文字,更无正切表可查,当然不知道tan∠O的值.然而侗族人民从长期的实践中发现,只要给定一个常数C,用OBi分别去乘以C,就可以把AiBi求出来.在调查中,发现侗族人民实际生活中早就有了专门计算直角三角形对边的通用公式,即:
直角三角形的对边=直角三角形的邻边×C(C为正常数).
根据实际需要C可以取不同的值,聪明的侗族从长期的实践经验中发现风雨桥人形架中应取C=0.75.但侗族语言中没有纯小数,碰到整数部分为0时,将其放到下一个单位进行运算.于是取C=7.5,用市尺将OBi(i=1、2、3、4)表示出来,再分别把它们代入上式,就可以求出AiBi的长,且它们的单位是“寸”.这就是侗族人民在实际生活中处理纯小数问题常用的方法.

图12
而图11在实际制作中,常做成如图12那样的流线形屋面,曲线尽可能接近摆线,这样的设计不仅使建筑给人感观上的美,而且能以最快的速度排水.
在风雨桥亭、塔建筑中,无论是四角、六角或八角亭、塔,近似计算都是无法回避的事实.例如,用比例的方法得到正八边形,就是属于近似计算问题.还有运用公式(2)计算正方形的边长就是一个取边长的不足近似的近似计算,误差不超过0.018cm,在半径不超过3m的塔顶上误差不会超过5.4cm;建筑师傅对这样的误差全凭借长期的做工经验,并根据柱头的大小、半径的长短来估计误差大小进而去弥补不足,同时还利用杉木的韧性将连接两柱头的木枋做成如图13的两个“鱼尾”弥补其不足,“鱼尾”又起到掩盖柱眼以增强建筑的美感和固定柱子位置的作用.真可谓巧夺天工.

图13
4 风雨桥建筑中平移和曲线逼近的思想方法

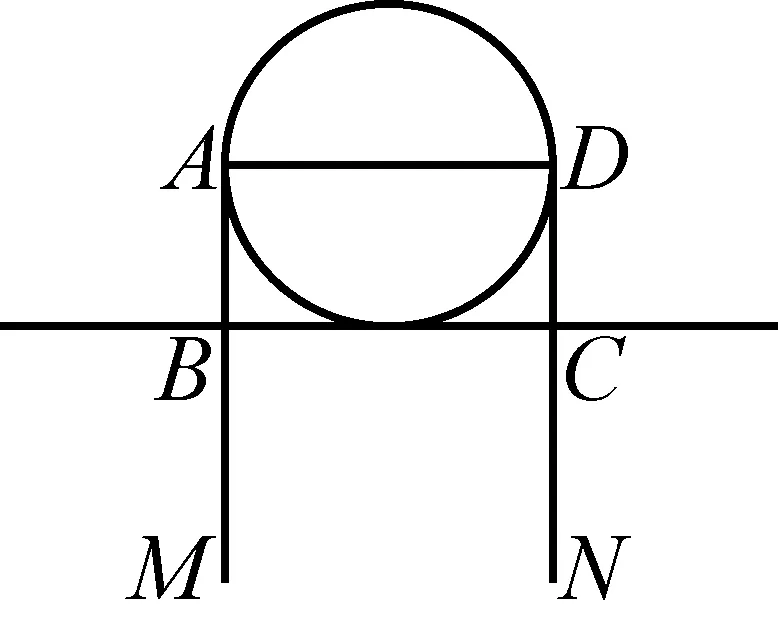
图14

图15

图16
5 风雨桥建筑中的平面镶嵌
图17是侗族风雨桥窗户的花格,显然,它也是由正三角形和正六边形两种镶嵌成的一个平面,所不同的是,此时的正三角形的边长是正六边形边长的两倍.这为研究者研究当正三角形的边长是正六边形边长的n倍时能镶嵌成一个平面(图18)提供了现实模型.

图18
6 风雨桥建筑中的对称变换
图19是侗族风雨桥上窗户花格,虽然每一种窗户上的花格各不相同,但在这些纷繁复杂的图案中都具有一个共同的特征那就是对称性.这说明对称性在侗族的建筑中得到了广泛应用.

(1) (2) (3) (4)图19
综上所述,侗族特有的桥梁建筑风雨桥,它承载着侗族数学文化的发展,从侗族风雨桥建造技术中所对数学的基本运算及一些数学思想在实践中的应用所表现出古朴的数学思想.
侗族风雨桥的历史悠久,它汇集了侗族的信仰与理想,珍藏着民族的智慧与力量,是侗族千百年来不断创新发展卓越的建筑杰作.因此风雨桥建筑技术中反映了古代侗族人民对古朴数学有了较好的理解和应用,她把侗族古老的数学思想融入建筑应用中,以建筑艺术作为载体并很好的传承了人类古老的数学文化.

