耳片接头的断裂失效数值模拟

林长亮，胡文刚，刘娜

(航空工业哈尔滨飞机工业集团有限责任公司 飞机设计所，哈尔滨市 150066)

0 引 言

20世纪50年代，强度许用值用来校核结构件的安全性能，大多数的强度计算都是检查结构的工作应力值是否在许用值之下。这种方法对结构的强度校核工作起到很大的推动作用，至今仍在结构设计领域广泛的应用[1]。但是在将近一个多世纪的结构制造生产应用中发现，在一些特定的工作环境下，采用强度许用值作为设计条件制造出的结构件并不安全。很多结构在低于许用值情况下，出现了严重事故。尤其是火车轨道、压力容器、储藏罐、管道等受高低周疲劳载荷作用，以及在低温或腐蚀环境中工作的结构。

1943-1947年，二次世界大战期间，美国拥有的5 000艘焊接船中，据统计有将近20%的船只出现了断裂事故，其中4%的船只完全报废。1949年美国Ohio的天然气工厂制造的天然气液态存储罐发生爆炸，强烈的爆炸力摧毁了一大片建筑，许多街区瞬间变为废墟。50年代初，美国制造的北极星导弹，其使用的高强度钢屈服值为1 372 MPa,但在工作应力只有686 MPa的情况下出现了爆炸，美国北极星固体导弹固体燃料发动机壳体在试验时发生爆炸[2]。20世纪80年代，挪威北海的海洋平台由于撑杆折断沉入大海[3]。因此断裂力学作为一门研究有缺陷构件的断裂强度学科，就是为了拟补传统设计的这一严重缺陷而产生的。

目前，国内外学者对断裂力学的应用都做了大量研究工作。Ahmad Rahbar等[4]采用线弹性断裂力学理论，研究了腐蚀对管道接头裂纹扩展寿命的影响，结果表明：点蚀的位置和几何形状是影响应力强度因子的主要参数。Okada Takao等[5]对搅拌摩擦焊接接头在飞机中的应用进行研究，发现焊接条件对材料的硬度分布、静态强度和断裂位置均有影响。R.Cagri Kutlubay等[6]研究了骨折治疗中，动态弯曲力作用下接头的疲劳强度，发现压螺钉远离骨折线时，板、螺钉和骨组成的关节疲劳强度会降低。Gao Shan[7]建立了延性金属断裂模型和混凝土损伤塑性本构的有限元模型，提出了一种将预应力荷载应用于刚节点螺栓准静力分析的方法。Ikechukwu Onyegiri等[8]采用脆性断裂准则，评估了夹芯管接头的临界载荷，利用应力集中系数(SCF)确定了安装过程中潜在的关键缺陷位置，并对其严重程度进行评估。Ahmed Bensari等[9]采用断裂力学理论，研究了结构止裂效应的判据。Kristen Rege等[10-11]采用有限元法计算薄壁结构在拉扭作用下的应力强度因子，计算结果表明：基于薄壳理论的扭转载荷解析解对于薄壳的长裂纹是非保守的，给出了避免出现大范围裂纹的解决方案；并对XFEM法和FEM法在疲劳裂纹扩展中的计算进行系统性的介绍。

叶波等[12]采用LS-DYNA对静态和冲击荷载作用下的含裂纹半圆弯曲(SCB)实验进行数值模拟。根据静态实验的模拟结果，提出适合复合型加载的Ⅰ型应力强度因子拟合公式。王谊清等[13]通过化学成分、热处理工艺、材料缺陷和试验件取样对碳钢和低合金钢的断裂延性性能测试造成的影响进行研究。肖玲等[14]对Fe基软磁复合材料的断裂性能进行研究，提出通过保持涂层覆盖完整和热压的方式来提高复合材料的断裂性能。王贺郑等[15]通过对多种规格的滚扎直螺纹的动态力学性能试验，总结了钢筋接头疲劳断裂的原因和规律。胡蓓雷等[16]采用四分之一奇异有限元法，建立了混凝土复合型裂纹有效断裂准则。杨志锋等[17]采用扩展有限元和传统有限元计算拉伸样件的J积分，并与试验结果进行对比。杨学等[18]通过应力场结合试验结果，得到四种金属材料的应力三维度准则中的相关参数。王雪明等[19]通过复合材料层合板不同裂纹深度的三点弯曲试验，分析复合材料的弯曲断裂特性，提出了J积分表征复合材料层合板的断裂韧性是可行的。杨杰等[20]使用GTN损伤模型，计算不同约束状态下双金属接头界面裂纹的J-R阻力曲线和延性断裂，建立双金属接头表征参数与断裂延性之间的关系曲线。

综上所述，已有的研究多是关注材料的断裂性能参数算法，经典试样[21]的表征参数与延性断裂的关系，对于耳片接头类结构的延性断裂研究较少。本文根据接头材质的力学性能特点，基于延性断裂准则中的应力三轴度算法，计算单耳片接头结构的断裂载荷，给出位移-载荷曲线，并将试验结果进行对比。

1 基本原理

延性断裂理论指出，材料的延性断裂是由于构件内部的初始缺陷引起的，因为构件在加工过程中，都会由于制造工艺条件的限制以及材料本身的性质存在微观孔洞和裂纹。金属构件在外部大载荷的作用下，材料进入塑性区，构件内部的微孔洞聚集成核生长逐渐形成裂纹，当裂纹扩展到构件表面时，构件发生断裂。延性断裂准则一般采用断裂阀值作为判据计算结构在承载过程中是否发生断裂，因此断裂准则的选择和断裂阀值的确定对预测结构件断裂位置和断裂载荷有重要作用。

表1 延性金属断裂准则

准则9中：

w1=(1-aσm)-a

w2=(2-A)β

A=max(S2/S3,S2/S1)

其中，σ1，σ2，σ3，S1，S2，S3为从大到小的3个主应力以及3个主应力偏量；a,k,β为材料常数；C为断裂阀值。

本文主要使用应力三轴度(CONT)准则分析计算耳片接头的单向拉伸断裂失效。

2 拉伸破坏试验

使用万能试验机对4种接头结构进行单向拉伸试验。4种接头试件的底座尺寸统一为长80 mm，宽60 mm，接头耳片处螺栓孔直径为12 mm，底部螺栓孔直径6.2 mm。以凸台接头为例，其尺寸如图1～图2所示。

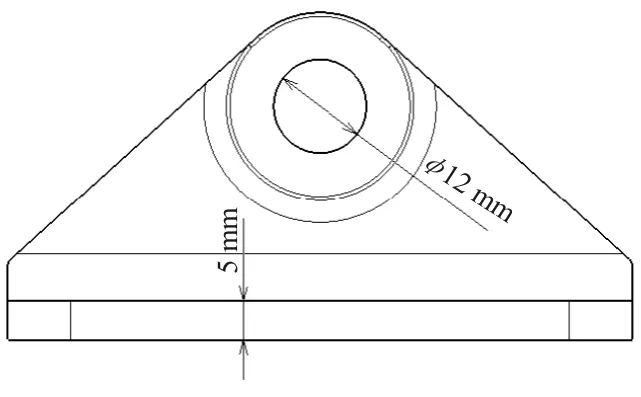
图1 凸台接头尺寸

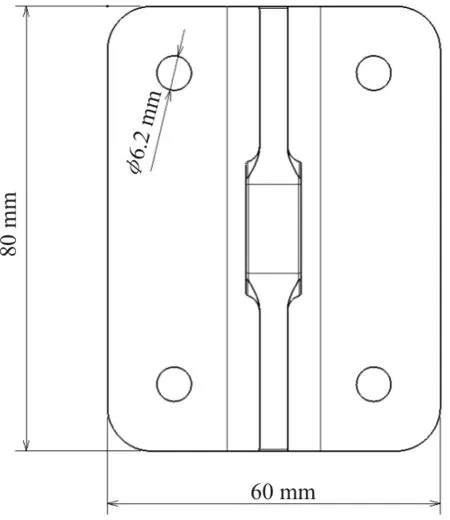
图2 凸台接头尺寸

4种接头的主要不同尺寸部位如图3所示，尺寸数据如表2所示。

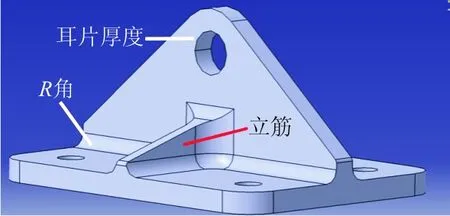
图3 接头主要不同尺寸部位示意图

编号R角/mm立筋耳片厚度/mm13无526有536无746无10(凸台)

试件底座通过假件固定到试验机上，耳片处使用连接螺栓进行单向拉伸加载。为了保证加载精度，按每次增加500 N载荷逐级加载，直至试件发生破坏，试验件安装如图4所示。耳片接头的位移-载荷曲线使用万能试验机测量。

图4 接头拉伸试验

3 有限元建模

3.1 模型边界条件

本文依据拉伸试验情况建立了接头的有限元模型。使用C3D8R类的六面体体元对接头结构进行网格划分，以耳片处的螺栓孔圆心为参考点，对圆孔施加MPC，在圆心处施加拉伸载荷50 000 N。底部四个圆孔用X，Y，Z、RX，RY，RZ6个方向来模拟螺栓的约束，接头有限元网格模型如图5所示。

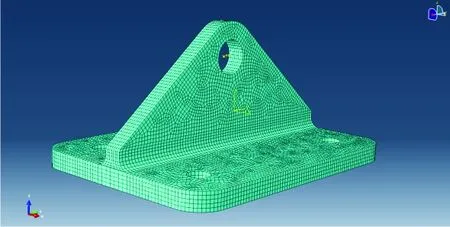
图5 接头有限元模型

在仿真中，通过确定接头发生断裂时的时间来计算仿真中接头发生断裂时的载荷数值，载荷计算公式如式(1)所示。

(1)

式中：F为接头断裂载荷；F0为在ABAQUS中设置的总载荷；T为接头在仿真计算中发生断裂时的时间；T0为在ABAQUS中设置的总载荷作用时长。ABAQUS中设置的时间-载荷曲线如图6所示。

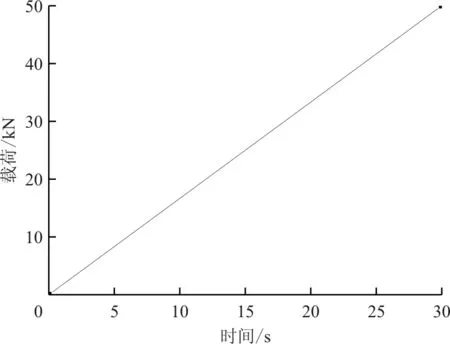
图6 时间-载荷曲线

3.2 材料本构

在ABAQUS中，需要对材料的应力三轴度和破坏应变值进行计算。应力三轴度是结构件静水压力与Mises等效应力的比值。

静水压力公式：

Mises等效应力公式：

式中：σ1，σ2，σ3为主应力。

断裂应变的计算公式为

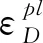
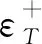
接头的材料为2024铝材，2024铝材的应变-应力三轴度曲线如图7所示。

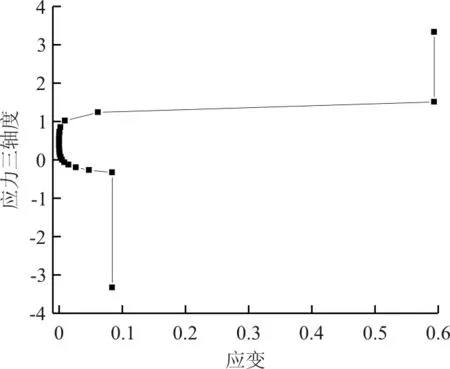
图7 2024铝材应变-应力三轴度曲线

4 仿真结果与试验结果对比

4种构型接头的计算结果如图8～图9所示，可以看出：仿真计算断裂的位置与试验断裂位置基本一致,都是在耳片孔的中间位置。试验件断裂面平齐，仿真结果的断裂面属于剪切断裂。这是由于在试验中，试验件存在一定的装配间隙，试件在拉伸过程中有一定程度的侧向弯曲应力，导致加载面整体在承弯抗剪的作用下断裂。本文有限元模型使用的约束是刚性模拟，无法模拟间隙造成的接头弯曲现象。

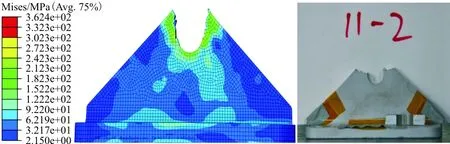
(a) 1号接头试件断裂位置仿真与试验结果对比

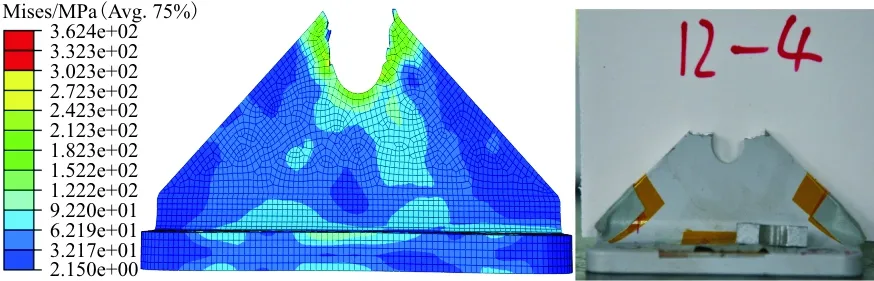
(b) 2号接头试件断裂位置仿真与试验结果对比

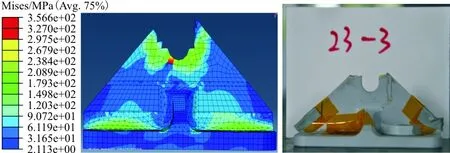
(a) 3号接头试件断裂位置仿真与试验结果对比

(b) 4号接头试件断裂位置仿真与试验结果对比

从图8～图94种接头构型的试验与计算值的载荷-位移曲线如图10所示。

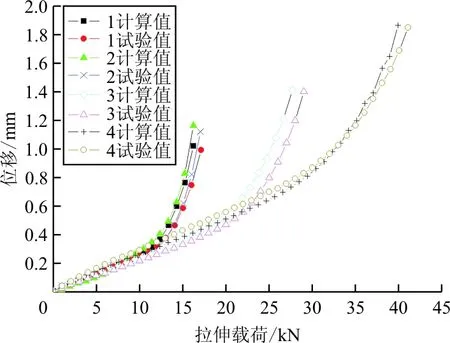
图10 4种接头的载荷-位移曲线

4种接头的断裂载荷计算值与试验值误差对比如表3所示。

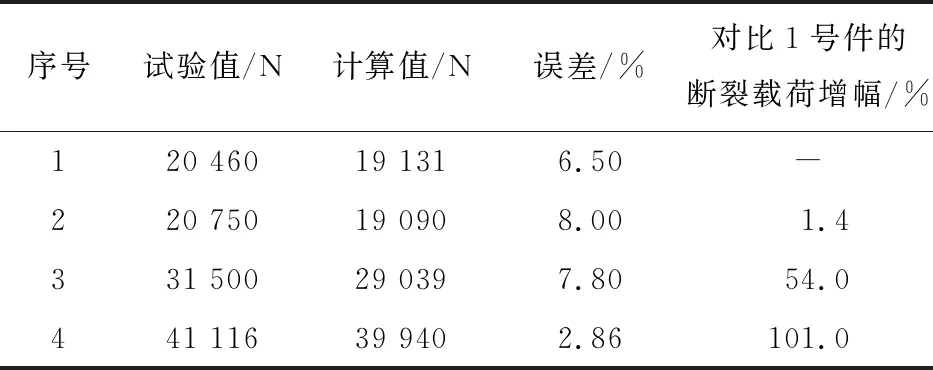
表3 断裂载荷的计算值与试验值对比

从图10和表3可以看出：对比1号接头R角为3 mm，无立筋的接头结构，增加耳片的厚度可以提高接头的断裂性能，最大增幅可为101%。4种接头构型在初始加载阶段的位移变形基本一致，呈线性变化，当载荷加载到12 000 N，材料进入塑性阶段后，结构的变形进入了非线性阶段，表明接头线性阶段的位移变形只受材料的力学性能影响，结构形式影响较小。

5 结 论

(1) 通过仿真与试验结果的对比，本文采用的应力三轴度算法精度较高，材料参数的准确性和试验条件的合理模拟是保证计算结果可靠性的必要条件。

(2) 接头的断裂位置主要在耳片的中心位置，断面形状受到试验、材料本构、边界条件等因素的影响。

(3) 接头在线性阶段的位移变形只受材料力学性能的影响，受结构形式影响较小。