基于拓扑优化的新能源汽车摆臂轻量化设计

黄福洲 蔡剑 王德远 孙辉 吴泽勋

摘要：为对某新能源车型前悬挂下摆臂进行结构轻量化设计，运用悬挂动力学模型提取摆臂各连接点在各工况下的静载荷，结合拓扑优化分析方法，获得摆臂的最佳传力路径和材料分布，明确轻量化优化方向。优化结果表明，优化后的摆臂强度满足设计要求，质量减小27%。

关键词：新能源汽车;下摆臂;拓扑优化;轻量化

中图分类号：U463.335;TB115.1

文献标志码：B

文章编号：1006-0871（2019）02-0038-04

0 引 言

目前，各国关于汽车环保的法规要求越来越严格。为降低汽车能耗、增加汽车续航里程，汽车轻量化已成为汽车研发的重点。国内外各大企业都投入高额的研发经费，通过结构优化设计和新材料的运用，对汽车轻量化进行多方位的研究，并已经取得显著成果。[1-3]摆臂是汽车悬挂系统的重要零部件，承受着复杂变化的载荷。在汽车行驶过程中，路面传递给车轮的载荷通过摆臂传递到车身。同时，摆臂与副车架连接硬点的布置和衬套方向的选择，都对汽车的操控性和稳定性有重要影响。[4]

本文对某新能源车型的前悬挂下摆臂进行研究，在保证强度和工艺满足设计要求的情况下，进行轻量化设计。

1 摆臂强度载荷

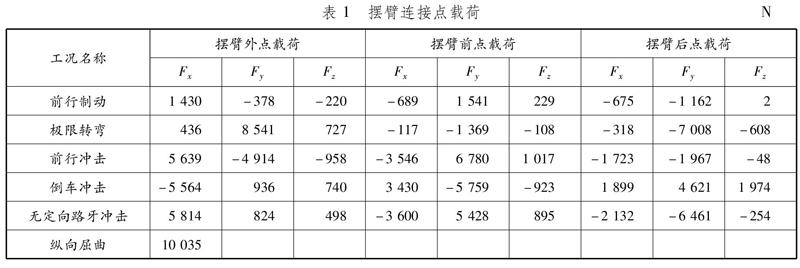
运用多体动力学软件Adams/Car搭建前悬挂动力学分析模型，根据整车和悬挂参数，结合摆臂强度工况，搭建前悬挂静态仿真模型，提取摆臂各连接点的载荷，为拓扑优化和强度校核提供输入。分解后的摆臂连接点载荷见表1。

2 摆臂拓扑优化设计

优化设计贯穿于整个零部件设计研究过程中，能帮助工程师在众多的方案中寻找最优的设计方案。常用的优化方法主要有拓扑优化、形貌优化、尺寸优化和形状优化等，其中拓扑优化由于其创新性和算法先进性，被广泛运用于结构优化设计中。近年来，铝合金、镁合金等轻量化材料在汽车制造中的运用比重越来越高，因此对零部件进行优化分析意义重大。

2.1 拓扑优化基础理论

结构拓扑优化是在指定设计空间内寻找结构的最佳传力路径和最优材料分布的一种优化方法。[5-6]在进行结构拓扑优化设计时，将设计区域的结构离散成足够多的单元，再运用优化策略和准则，将不重要的单元从结构中去除，剩余的单元即为结构在指定工况下的最优拓扑结构。目前，最常用的拓扑表达形式和材料差值模型方法有均匀化法、密度法和变厚度法等。

OptiStruct拓扑优化的材料差值模型采用密度法。该方法将有限元模型设计区域内每个单元的密度作为设计变量，该密度值在0～1范围内连续变化，并且在单元密度与单元材料的弹性模量E之间建立函数关系。[7]优化后的单元密度接近于1，表示该单元处的结构是主要传力路径，必须保留;优化后的单元密度接近于0，表示该单元不是结构的主要传力路径，可以去除该处结构的材料。

2.2 OptiStruct拓扑优化流程

优化设计有三要素，即设计变量、目标函数和约束条件。设计变量是指改变其值的大小从而可提高结构性能的一组参数;目标函数是指产品的最优性能，是设计变量的函数;约束条件是指在优化过程中必须满足的一些参数和性能要求。

式中：X=（x1，x2，…，xn）为设计变量，如产品结构的材料厚度、截面形状等;f（X）为设计目标，如产品的各种力学性能、总质量或者柔度等;g（X）和h（X）为需要进行约束的设计响应，如结构的1阶模态频率、某点的位移或者某个部件的最大应力等。

OptiStruct运用数学规划的方法，通过计算灵敏度构造近似显式模型，采用小步长迭代寻找最优解，是工程上高效和稳定的优化算法。[5]OptiStruct内部拓扑优化流程见图1。

3 汽车摆臂拓扑优化

3.1 拓扑优化模型

在进行拓扑优化前，先建立符合要求的有限元模型。虽然摆臂为钣金冲压结构，但考虑到拓扑优化的效果，采用尺寸为1 mm的1阶四面体单元建模，并保证厚度方向上至少分布3层单元。摆臂安装点受力复杂，因此在进行拓扑优化设计时，将安装点附近以外的区域定为设计空间。摆臂拓扑优化模型见图2。

3.2 拓扑优化参数

载荷工况的选择对拓扑优化分析结果的影响较大：当工况定义不全面时，摆臂的主要受力特点易被忽略，拓扑优化结果将为不合理的传力路径;当工况选择过多时，拓扑优化的收敛难度和计算时间增加，而且容易给出偏保守的优化结果，不利于为轻量化设计提供参考。因此，合理选择拓扑优化载荷工况至关重要。由摆臂连接点载荷可知，摆臂主要承受纵向力和横向力，因此拓扑分析选择摆臂纵向力和横向力较恶劣的前行制动、极限转弯和倒车冲击3个工况。

将体积分数上限设为0.3，作为约束条件;目标函数是考虑3个载荷工况的权重柔度最小，即整体刚度最大化。考虑到摆臂纵向刚度的重要性，选择前行制动、极限转弯和倒车冲击3个载荷工况的权重因数依次为0.4、0.2和0.4。摆臂为钣金冲压结构，不考虑拔模约束。

3.3 拓扑优化结果

经计算，拓扑优化后摆臂的最佳传力路径和材料分布见图3，权重柔度收敛曲线见图4。图3圈中显示为单元密度不大于0.3的结构，

可认为此区域不是摆臂的主要传力路径，所以区域1、2、3和4的材料可被去除，这些区域是后续轻量化优化设计的重点区域。

目标函数权重柔度是考虑3个工况的权重因数后的柔度加权和。从权重柔度收敛曲线可以看出，结构的总柔度在40次迭代后收敛，说明摆臂的刚度在满足设计约束條件时达到最大，此时设计区域的单元密度分布即为结构的最佳材料分布。

4 摆臂结构优化

4.1 摆臂轻量化设计

根据拓扑优化结果，重点对图3中的4个区域进行改进。区域1、2、4位于翻边处，翻边的前后与衬套和球头安装点相连，是关键位置，因此将翻边中间的高度适当减小，并设置圆形过渡，避免应力集中。区域3为加强筋处，此处添加直径为32 mm的减重孔，并结合单元密度云图，将摆臂本体厚度由3.0 mm减为2.5 mm。优化后的摆臂结构见图5。

4.2 摆臂强度分析

为验证轻量化设计后摆臂的性能是否满足要求，结合强度工况和材料应力-应变曲线，对其进行强度分析。摆臂材料为冷成型热轧汽车结构钢板QSTE420TM。摆臂强度分析结果见表2和图6～7。摆臂应力最大工况为无定向路牙冲击工况，最大应力位置位于摆臂外点与转向节连接翻边处，最大应力值为439.0 MPa，最大纵向屈曲载荷为12 446 N，均满足强度要求。

5 结 论

（1）基于摆臂早期结构设计，进行拓扑优化分析和轻量化设计，优化后摆臂强度和屈曲性能均满足设计要求，摆臂质量由1.89 kg减至1.38 kg，减重约27%。

（2）拓扑优化可有效分析摆臂的最佳传力路径和材料分布，为轻量化优化提供合理的方向。

参考文献：

[1] KRISHNA M M R， ANDERSON S V. Shape optimization application in upper control arm design[C]// Proceedings of SAE 2000 International Truck & Bus Meeting & Exposition. Portland：SAE International， 2000. DOI：10.4271/2000-01-3445.

[2] KRISHNA M M R.， STANGE A. Topology and classical shape optimization of a lower control arm：A case study[C]// Proceedings of ASME 2006 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. Philadelphia：ASME Press. 2006：127-132. DOI：10.1115/DETC2006-99173.

[3] 王登峰， 黄亚威， 秦民， 等. 轿车悬架控制臂参数化建模及轻量化多目标优化设计[J]. 汽车技术， 2015（1）：1-4.

[4] 宗长福， 郭孔辉. 汽车操纵稳定性的研究与评价[J]. 汽车技术， 2000（6）：6-9.

[5] 羅震， 陈立平， 黄玉盈， 等. 多工况下连续体结构的多刚度拓扑优化设计和二重敏度过滤技术[J]. 固体力学学报， 2005， 26（1）：30-35.

[6] 赵红伟， 陈潇凯， 林逸. 电动汽车动力电池仓拓扑优化[J]. 吉林大学学报（工业版）， 2009， 39（4）：846-849.

[7] 洪清泉， 赵康. OptiStruct & HyperStudy理论基础与工程应用[M]. 北京：机械工业出版社， 2012.

（编辑 武晓英）