脉冲等离子体推进系统模态分析和试验验证
代鹏 王尚民 张天平 李兴坤


摘要:利用HyperMesh建立脉冲等离子体推进系统的网格模型,应用Abaqus完成模态分析,采用力锤法进行模态试验,得到脉冲等离子体推进系统的模态和振型。有限元分析和试验测试数据的对比结果表明,脉冲等离子体推进系统有限元模型的模态与实际产品的模态误差在2%以内。分析结果验证推进系统有限元模型的合理性,可为后續正弦振动、随机振动和冲击谱响应分析的正确性提供保障。
关键词:脉冲等离子体推力器;模态;HyperMesh;Abaqus;力锤法;有限元
中图分类号:V439.2
文献标志码:B
文章编号:1006-0871(2019)02-0015-04
0 引 言
微纳卫星具有体积小、质量轻、结构简单、制造成本低等优点,近年来被广泛应用于遥感、通信、侦查等传统卫星应用领域。[1]然而,受总质量和总功率限制,传统的化学推进系统已无法满足微纳卫星轨道提升和维持、位置和姿态保持、阻力补偿,以及星座相位控制等空间任务。与化学推进相比,电推进技术利用电能产生并加速带电粒子,形成高速等离子体,喷气速率比化学推进高1个数量级,寿命长且无污染。这使得采用电推进技术进行轨道机动和位置保持成为当今先进卫星的重要标志。[2]
脉冲等离子体推力器(pulsed plasma thruster, PPT)是一种电磁推进器,具有功耗低、比冲高、结构简单和质量轻的优点,是当前国际上微纳卫星应用的主流推力系统之一。美国、日本和俄罗斯等国已在PPT的理论研究和空间应用中开展大量工作。[3-5]国内关于PPT的研究始于20世纪70年代,中国科学院电工研究所、国防科技大学、北京理工大学和兰州空间技术物理研究所都已开展PPT的相关研究。[6-9]兰州空间技术物理研究所是国内电推进系统研究的主要单位,根据航天任务需要,该所正在开展PPT工程样机的研制及其性能试验验证。对于在空间运行的航天产品,其在发射和太空飞行过程中需面临振动、冲击、噪声、加速度和微重力等复杂情况。为保障安全,根据航天产品抗力学环境的要求[10],在进入空间飞行前,PPT需要在地面接受一定条件的正弦振动、随机振动和冲击谱响应试验,并且确保试验后结构和性能完好。对于空间飞行产品,若外部振动激励与结构的固有频率相同,振动过程中产生的共振可造成结构的严重破坏。因此,有必要在研制阶段开展相应的仿真分析,确定PPT的模态,提前规避设计缺陷。此外,在采用模态叠加法进行正弦振动、随机振动和冲击谱响应仿真分析中,模态分析的准确性直接影响仿真分析结果的精度。因此,对PPT进行模态分析,研究其固有频率和振型,对预防共振和保证后续的振动响应分析具有重要的意义。
1 脉冲等离子体推进系统结构及其工作原理
脉冲等离子体推进系统由电源处理单元(power processing unit, PPU)模块和PPT模块组成,其中PPT模块包括储能电容、进给弹簧、推进剂、阴极板、阳极板和火花塞等。脉冲等离子体推进系统实物见图1,其中上外壳部分为PPT模块,下外壳部分为PPU模块。
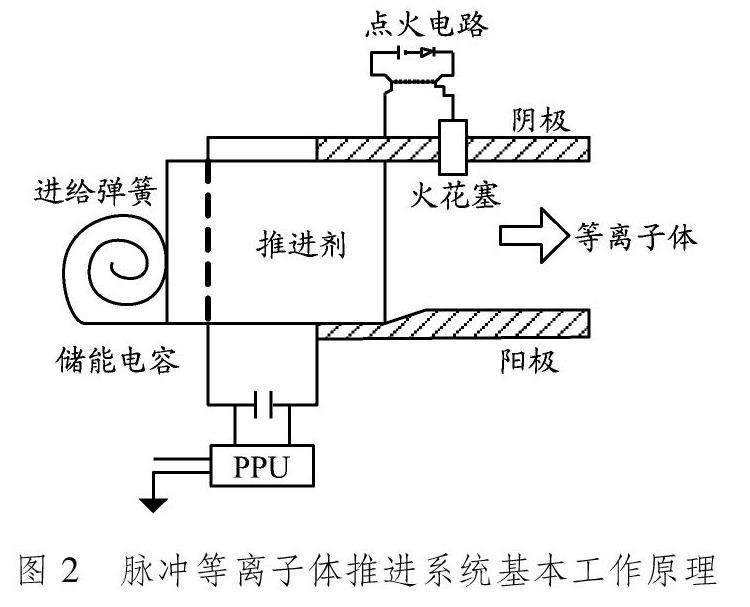
脉冲等离子体推进系统的基本工作原理为:储能电容充电到数千伏,与其相连接的电极板两端达到工作电压;在点火电路的作用下,电路中的火花塞产生等离子体放电,诱导电容在阳极板和阴极板间产生放电;放电后形成的高温电弧将推进剂表面薄层烧蚀并电离,形成等离子体;PPT阳、阴极板间的交变电场产生垂直于电场和带电粒子速度方向的感应磁场,带电粒子在磁场的作用下产生洛伦兹力;未被电离的推进剂在放电过程中被加热后加速流动;在热力和洛伦兹力的共同作用下,PPT将等离子体和烧蚀物一起喷出,产生一次脉冲推力;储能电容继续充电进行下一次脉冲工作。脉冲等离子体推进系统的基本工作原理见图2。
2 模型建立
在Pro/ENGINEER Wildfire 5.0中建立脉冲等离子体推进系统的实体模型。根据推进系统的整体结构特点,在不影响计算结果的前提下对模型进行简化,将模型中的PPU模块进行质量等效替代,删除影响较小的螺栓、螺母和垫片,并对删除部件的质量进行平均化处理后添加到临近的组件。简化后的脉冲等离子体推进系统模型见图3。
将模型导入HyperMesh中进行几何清理和网格划分,并对各部件进行材料和单元属性的定义。脉冲等离子体推进系统模型的主要参数为:上下外壳为2A12铝合金,其弹性模量为72.0 GPa,泊松比为0.31,密度为2 770 kg/m3;内部的推进剂为聚四氟乙烯,其弹性模量为4.5 GPa,泊松比为0.22,材料密度为2 200 kg/m3;采用实体单元建模,单元类型设定为C3D10和C3D8单元,网格划分后模型共有255 413个单元、225 544个节点。在HyperMesh中建立的脉冲等离子体推进系统有限元模型见图4。
将网格模型导入Abaqus中,根据模型中各个组件的连接关系,将螺钉固定的组件看作理想固定,采用Tie命令连接,各组件之间没有相对运动。整个模型采用通用接触定义,接触属性为光滑接触。采用力锤法进行模态测试,并将模态仿真分析中的PPT设置为自由无约束状态。
3 模型计算
3.1 理论基础
由振动理论可知,系统以某个频率振动时呈现的振动形态即为模态。模态分析的关键是计算结构的模态和固有频率。PPT振动系统的动力学模型[11]为
模态是结构本身的固有特性,与外部载荷无关,所以式(1)中F(t)=0。阻尼对PPT结构的固有频率和振型影响不大,可忽略式(1)中的阻尼项c。因此,动力学方程可简化为
式(5)展开后可得到关于ω2的矢量解,称为角频率。由频率与角频率的关系f=ω/2π,可以得到PPT结构的固有频率。
3.2 计算结果和分析
运用Abaqus中提供的特征求解方法对脉冲等离子体推进系统模态进行分析,在Frequency中采用计算精度较高、运算速度较快的Lanczos法提取模态。该方法能够避免PPT结构特征值在求解过程中丢失。[12]在Abaqus中提取模型前10阶模态和振型。由于模型处于自由状态,前6阶模态为6个自由度的刚体位移模态,所以脉冲等离子体推进系统结构的固有模態从第7阶开始。系统的4阶固有频率和振型特征见表1,各阶固有模态见图5~8。
从仿真分析的模态结果可以看出,脉冲等离子体推进系统的频率均较高,满足航天器产品基频大于100 Hz的要求,说明推进系统结构具有良好的刚度。
4 试验验证对比
有限元建模过程对倒角、螺栓和PPU进行简化处理,并且在接触关系的定义中采用理想的固定黏结,与真实推进系统结构有些差异。为掌握脉冲等离子体推进系统的真实动力学特性,修正有限元分析模型,在进行正弦振动、随机振动和冲击谱响应仿真分析前,采用力锤施加冲击激励的方法测试脉冲等离子体推进系统的模态。模态测试系统示意见图9。测试系统主要由固定架、柔性绳、力锤、加速度传感器、数据采集设备和模态分析系统组成。
在推进系统的外壳底部和右侧面粘贴加速度传感器,采用力锤在靠近推进系统喷口处的外壳向下施加脉冲力激励,数据采集设备采集响应点上加速度传感器的测量结果,然后传递到模态分析系统中,由响应点的频率响应曲线识别推进系统的模态参数。试验采用美国Dytran公司的3056B1加速度传感器和5800B4力锤,美国DataPhysics公司的70752数据采集设备和SignalCalc730模态分析系统。推进系统模态试验中锤击点和响应点的具体位置见图10。
数据采集系统采集到的右侧面(响应点1)和外壳底部(响应点2)的频率-加速度响应曲线分别见图11和12。
从图11和12中可以看出,在力锤的冲击激励下,测量点1和测量点2分别在频率为276.3和398.8 Hz时开始振动。测量点1振动时为脉冲等离子体推进系统的第7阶振型,频率值为推进系统的基频;测量点2振动时为第10阶振型。对比有限元分析结果可知:模态试验结果与有限元分析结果吻合较好,第7阶模态的误差为1.80%,第10阶模态的误差仅为0.29%。
5 结 论
利用HyperMesh建立脉冲等离子体推进系统的有限元模型,在Abaqus中计算其前10阶模态,得到推进系统的固有模态和振型。脉冲等离子体推进系统的试验基频为276.3 Hz,满足航天产品1阶频率大于100 Hz的要求。采用力锤法进行推进系统的模态试验测试,仿真分析与试验结果吻合良好,误差均小于2%。对比结果验证脉冲等离子体推进系统仿真模型的合理性,可为后续正弦振动、随机振动和冲击谱响应分析提供精确的模型,对脉冲等离子体推进系统结构的抗力学设计具有指导意义。
参考文献:
[1] 马定坤, 匡银, 杨新权. 微纳卫星发展现状与趋势[J]. 空间电子技术, 2017, 14(3):42-45.
[2] 田立成, 王小永, 张天平. 空间电推进应用及技术发展趋势[J]. 火箭推进, 2015, 41(3):7-14. DOI:10.3969/j.issn.1672-9374.2015.03.002.
[3] GUMAN W J, NATHANSON D M. Pulsed plasma microthruster propulsion system for synchronous orbit satellite[J]. Journal of Spacecraft and Rockets, 1970, 7(7):409-415. DOI:10.2514/3.29955.
[4] POPOV G A, ANTROPOV N N, KAZEEV M N, et al. Pulsed plasma thruster propulsion technology for small satellite[EB/OL]. (2003-02-21)[2018-11-20]. http://erps.spacegrant.org/uploads/images/images/iepc_articledownload_1988-2007/2003index/0040-0303iepc-full.pdf.
[5] TAMURA K, IGARASHI M, KUMAGAI N, et al. Evaluation of low power pulsed plasma thruster for μ-labsat II[EB/OL]. (2002-07-10)[2018-11-20]. https://arc.aiaa.org/doi/book/10.2514/MJPC02. DOI:10.2514/MJPC02.
[6] LIU W X, AN S M. Digital measurement of discharge current peak value in pulsed plasma thruster[C]// Proceedings of International Electric Propulsion Conference. Alexandria:AIAA, 1985. DOI:10.2514/6.1985-2062.
[7] AN S M, WU H J, FENG X Z, et al. Space flight test of electric thruster system MDT-2A[J]. Journal of Spacecraft and Rockets, 1984, 21(6):593-594. DOI:10.2514/3.25701.
[8] LIU X Y, WANG N F, YUAN S Y, et al. Discharge reliability in ablative pulsed plasma thrusters[J]. Acta Astronautica, 2017, 137(8):8-14.
[9] 王尚民, 田立成, 张家良, 等. 微脉冲等离子体推力器放电过程和性能初探[J]. 中国空间科学技术, 2017, 37(5):24-32. DOI:10.16708/j.cnki.1000-758X.2017.0080.
[10] 张正平. 航天运载器力学环境工程技术发展回顾及展望[J]. 航天器环境工程, 2008, 25(3):233-236. DOI:10.3969/j.issn.1673-1379.2008.03.010.
[11] 张亚辉, 林家浩. 结构动力学基础[M]. 大连:大连理工大学出版社, 2007.
[12] 史东岩, 庄重, 高山, 等. 基于Abaqus的模态分析方法对比及验证[J]. 计算机辅助工程, 2013, 22(S2):432-435.
(编辑 武晓英)

