凸显本质，体现价值

王巍 钱蔚

“角的初步认识”这一内容是在学生已经初步认识了长方形、正方形和三角形的基础上学习的。对于二年级学生来说“角”并不陌生，然而他们对“角”的认识仅仅停留在生活中，对于从数学意义上来认识角，这是首次，是起始课。教材在编写时，注重直观性和可操作性，首先呈现生活中常见的带角的物品，引导学生从观察实物中的角开始，让学生初步感知角;接着从实物中抽象出角的几何图形，体现了从直观到抽象的过程，使学生通过直观、形象的观察建立角的表象，感知角的特征;最后，通过制作角使学生进一步认识角是有大小的。

“角的初步认识”从知识点的传授来看似乎比较简单，但数学教学不仅仅是教几个知识点，数学教学是能力的教学，思维的教学。对于以具体形象思维为主的二年级学生来说，认识角的几何形象是需要一个过程的，是有难度的。因为生活经验告诉他们，尖尖的就是角。如何让数学角在学生的认知中健康地孕育，如何不漏痕迹、不超标准地凸显数学角的本质，为进一步习得角的概念打好基础？我们数学组进行了探索與研究，并尝试进行本课的教学。

一、逐步抽象，建立角的表象

1.引入图形

师：出示五角星。小朋友们看，这是一个什么图形？为什么叫五角星呢？ （因为它有5个角。）

师：五角星是不是只有五个角呢？今天我们就从数学的角度来认识角。（揭题：角的初步认识。）

师：你能在老师的三角尺上指出一个角吗？（学生如果指着一个顶点，教师就在黑板上画一个点，问这是一个角吗？引导学生继续指，学生指出边，就画边。）

2.找出生活中的角

出示三角尺、纸工袋、红领巾图片。

师：生活中很多物体都有角，你能找到角吗？

学生书空，边数边说从这些物体面上分别可以找到几个角。课件中描出学生指出的角，以突出角有两条边和一个顶点。

3.抽取角的几何图形

师：为了更好地研究角，我们把刚刚在物体表面找到的角“请”下来。

师：这些平面图形长得都不一样，但都是角，说明他们有着共同的特征。请你仔细观察，你能说说角长什么样子吗？

生1：都有两条线。

生2：两条线都是直的。

生3：两条边都靠在一个地方。

师：是啊，两条边都靠在一起，就有了一个点，这个点叫角的顶点（板书），两条直直的线叫作角的两条边（板书）。

介绍：我们通常从角的一条边画一条弧线到角的另一条边做一个记号，表示角。以后我们看到角，也主动画上记号好吗？

师：小朋友们见过手电筒吗？手电筒可以射出一束光来。我们把手电筒的灯泡看作是角的顶点，任意选两条光线看成是角的两条边，这就是一个角。

谈话：你能指出这些角的各部分名称，并书空画出角的记号吗？

交流：这些角都有什么共同的特征？

小结：角有一个顶点和两条边。（板书）

【设计意图：学生在刚接触角时，只是凭生活中的经验来判断角的存在，在发现角的特征之前指角是比较困难的，教师设计了借助生活中的手电筒，动态演示从一点引出两条射线形成的角，将角的形成渗透在课中，进一步引导学生观察“点”和“边”的关系，使他们了解这个点其实是两条线连接的位置，角的两条线是从这个点出发引出来的。这样的体验显然能为以后进一步学习角的概念打好基础。】

4.辨认角，凸显角的特征

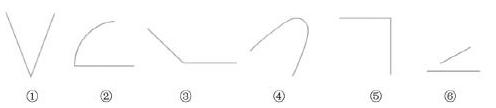
现在大家已经认识了角，请你做出判断，哪些图有角，用手势告诉老师。

聚焦，①③⑤号图形，你们怎么看出它们都是角呢？

生：因为它们都有一个顶点和两条直直的边。

师：抓住了角的特点，很捧，剩下的几个为什么不是角？

生1：②号图形有一条边是弯的。

生2：④号图形两条边都是弯的，它也没有顶点。

追问：⑥号图形两条线可都是直的，你能想个办法使它变成一个角吗？

小结：判断一个图形是不是角，关键要看什么？（一个顶点和两条直直的边）

5.数角

师：角是平面图形中的一员，角也是进一步认识其他图形的重要内容。现在请大家数数下面的图形中，各有几个角，请大家先做上角的记号，再填空。

学生独立填写，全班交流，重点交流第一个图形里有几个角。

对比呈现学生的正确答案和错误答案，引导学生进行思考。

抽取出三角形、四边形、五边形的图，增加六边形，让学生观察边与角的个数，发现什么？

师小结：几边形就有几条边、几个角。

【设计意图：学生经历“辨角”这样的活动过程，不仅能丰富学生对角的特征的感知，提升他们对角的整体识别能力，而且有助于他们在头脑中主动构建角的表象，积累认识图形的经验，发展初步的空间观念。“数角”后设计抽取、观察、发现的环节，旨在给学生提供一个自主构建知识的过程，让学生在具体的情境中概括出“几边形就有几条边、几个角”，培养学生梳理知识、构建知识的能力。】

二、观察发现，感受角的大小

1.动手做角

师：学到这，我们已经认识了角，会判断哪些图形是角，会数角了，想不想自己来做一个角？选择你喜欢的学具，开动脑筋，动手做角。 （学生自己选择学具，做角）

2.展示、交流

生1：我用小棒搭了一个角，这是角的顶点和两条边。

生2：我用圆片折了一个角。

生3：我拼了一个角，这个角能动。

师小结：同学们用不同的材料都做成了一个角，这些角都有一个顶点和两条边。

3.玩活动角

（1）感受角是有大小的。

师：（拿出一个活动角）老师这有一个角，老师的角和你们的角有什么不同？

生：一个大，一个小。

师：老师的角好大，同学们的角有点小，看来角是有大小的，是吗？为什么有的角大，有的角小呢？角的大小与什么有关呢？来，我们用手上的活动角做一个“变变变”的游戏。（师喊口令，生做。）

师：把你们的活动角拿在手里，（师也拿一个活动角）请变出一个比老师手上的角要大的角。再变大点，你是怎么做的？

师：把手上的活动角变小一点，再小一点。你是怎么做的呢？（把边合拢一点）

师：当拉成平角时，问学生，这还是角吗？ 为什么？

（2）动态演示角的另一种形成方式。

动画演示，钟面上时针和分针不停地转动，两根针就形成了一个角。

师：兩个钟面上有大小不同的角，你能看出上面哪个角最大，哪个角最小吗？

追问：你是怎么知道的？

小结：角的大小与两边张开的大小有关，两边张开得越大，角就越大。

【设计意图：静态角难以避免其边的长短以及表面上的大小所带来的非本质属性的干扰，所以教学中教师以学具“活动角”帮助学生理解角的大小，引导学生把注意力集中到边的张合中来，使其直观地感受到角的大小是与两边张开的角的大小有关。在操作、体验、思考、交流等活动中，学生清晰地了解到角是有大有小的，角的大小与两边张开的大小有关，两边张开角变大，两边合拢角变小，既发展了学生的空间感知能力，双让学生体会了活动角在生活中的应用价值。】

4.比较角的大小

师：老师这儿有两个活动角，你能比较出它们的大小吗？你是怎么比较的？

师小结：是呀，两边张开得越大，角越大。

师：（出示两个角）这两个角谁大谁小，该如何比较呢？（不能一眼看出）

生：我可以这样比。（学生上讲台操作）

师：这个同学将顶点放在一起，一边重合，看另一边的位置，比较得出了两个角的大小。

师：有两个同学分别在作业纸上画了角，哪个角大呢？

学生先独立思考，再交流。展示学生借助活动角来比较角的大小的图片。

指出：有些角的大小可以用观察法判断，有些无法用观察法判断，如果无法直接用两个角重叠的方法判断时，可以借助工具来测量。

多媒体出示两个同样大的角，一个角画出的两条边长，另一个角画出的两条边短。

师：你觉得这两个角哪个角大些？

生：一样大。

生2：角1大。

师：到底哪个角大呢，怎么办？

生：重叠在一起比一比。

课件演示验证，使学生观察到：角的大小与边的长短无关，再延长边，角的大小依然没变。

师小结：生活中的角两边长短是固定的，而数学上的角的两条边可以无限延长，角的大小与边的长短无关，与角度的大小有关。

【设计意图：设计有梯度的练习使学生会使用重叠法比较角的大小，而且能够提炼比较的方法“一是顶点重合，二是一条边重合，三是看另外一条边，谁的角度大谁的角就大”，使学生的数学知识与活动技能得到同步增长。最后借助活动角比较作业纸上两个角的大小，为学习量角奠定基础。通过猜一猜、移一移、比一比，使学生了解角的大小与边的长短无关这一知识点。】

三、拓展练习，提升对角的认识

1.一张长方形纸，剪去一个角，还剩几个角？

先让学生大胆猜测，再动手实践，全班交流。

2.数角

课件演示：一个顶点两条边，就组成了一个角，如果再加一条边呢？你能找到几个角？（如下图）

追问：如果难度升级，再加一条边呢？这其中会不会藏着什么数学秘密呢？

【设计意图：波利亚说，学习任何知识的最佳途径是通过自己去发现。因为这种发现，理解最深也最容易掌握其中的内在规律、性质和联系。练习的过程是学生头脑中“角的样子”进一步明晰的过程。有思维含量的练习，极大地激发了学生学习数学的兴趣。学生通过尝试，探索出其中蕴含的数学规律，也体验了成功的喜悦。】

师谈话：通过今天的学习，你觉得五角星上只有5个角吗？

指出：其实五角星除了这些角，还有其他角呢，到了中学，我们会进一步学习。

【设计意图：在学习本课之前，很多学生受生活经验的影响，认为五角星上有五个角。课尾，再次出示五角星，学生能够主动抓住角的本质特征，辨认出5个“空心角”。此时，教师告诉学生还有其他角，为后续进一步认识角奠定基础。】