聚焦数学模型思想 精心设计课堂教学
顾燕
摘要:《数学课程标准》指出:“模型思想的建立是学生体会数学和外部世界联系的基本途径。”模型思想是数学教学的十大关键词之一,模型思想的感知、发展、建构的过程,是数学知识与技能掌握和运用的过程,也是学生数学学习进步、提高、发展的过程。以苏教版《数学》二年级下册“两步计算的实际问题”为例,谈一谈教学时要如何聚焦数学模型思想,精心设计课堂教学:创设情境,感知模型——建模的起点;叙述思路,建立模型——建模的关键;比较反思,验证模型——建模的灵魂;实践应用,巩固模型——建模的延展。
关键词:模型思想;设计教学。
《义务教育数学课程标准(2011年级)》指出:“模型思想的建立是学生体会数学和外部世界联系的基本途径。”模型思想是数学教学的十大关键词之一,模型思想的感知、发展、建构的过程,是数学知识与技能掌握和运用的过程,也是学生数学学习进步、提高、发展的过程。以苏教版数学二年级下册“两步计算的实际问题”为例,谈谈教学时要如何聚焦数学模型思想,精心设计课堂教学,让学生学会发现和提出问题,分析和解决问题,进一步掌握数学知识与技能,积累数学经验与方法,逐步培养应用意识和创新意识。
一、创设情境,感知模型——建模的起点
教学时,可以把生活中常见的与数学学习有关的情境引入到课堂中,鼓励学生应用生活经验和数学知识去解决问题,在分析、抽象中逐步感知简单的模型思想。可以采用场景图的形式出示情境,激起学生的生活经验,让学生在情境中经历收集和整理信息的过程,把实际问题变得更数学化,从而提高学生对数学模型学习的兴趣。

如在导入时,可以创设生活情境:原有34人,上车5人,现在车上有几人?公交车开往下一站,又下车5人,离站时车上有几人?把这样的生活原型提炼为数学模型:原有的人数+上车的人数=现在车上的人数,原有的人数—下车的人数=现在车上的人数。这样的情境创设,不仅渗透了解决此类问题的简单的模型思想,又为例题中复杂的模型思想做铺垫。
在建立数学模型时,要注意在选择的生活问题上,要关注问题的典型性、代表性,创设常见的生活情境来丰富学生接触的数学模型。学生在生活中已经有了乘坐公交车的生活经验,可以在这样的生活情境中抽象出数学问题。教学时,先让学生说说条件和问题,再分析解决问题,悄然渗透模型思想,让学生在生动快乐的数学课堂中提升数学素养,这也是建模的起点。
二、叙述思路,建立模型——建模的关键
在研究教材时,可以从多角度来深入剖析,理解教材中的一些建模内容的思路编排,充分发掘其中蕴含的模型思想,绝不能在出示问题情境后直接让学生回答。因为,如果从生活情境直接到解决问题,那么在这个过程中就缺少了数学化的过程。所以,要特别重视叙述思路,这是在为学生搭建脚手架,将实际问题数学化,帮助学生建立数学模型。

如在新授时,可以在导入的基础上呈现例题:车上原来有34人,到站后有15人下车,又有18人上车,离站时车上有多少人?在解决像这样的经过两次变化后的实际问题时,可以先让学生充分讨论后,再叙述思路。在叙述思路的过程中,既要引导学生说清楚可以先算什么,再算什么,联系生活经验解释为什么可以这样算;又要关注学生在讨论后出现的不同想法,进行适时地提炼数学模型。从而,逐步建立初步的数学模型:可以先算下车后的人数,也可以先算上车后的人数,还可以先算上车比下车多的人数。
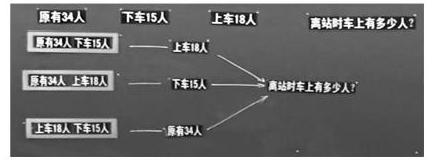
两步计算的实际问题中的数量关系是十分重要的,要学会分析学生思维的起点,找准思维的方向,帮助学生用数学语言分析问题。在叙述思路时,要学会放手让学生解决,尊重学生的自主性和创造性,帮助学生理解数量关系,并通过独立思考、合作交流,归纳抽象出解题思路,寻求解决方法,构建数学模型,这个过程正是建模的关键。
三、比较反思,验证模型——建模的灵魂
学生认识数学问题中的某种关系,一般需要经历直观操作、形象感知和逻辑抽象等阶段来完成。在认识这些解题思路的初始阶段,有效利用直观动作思维来呈现,有助于建立模型,让学生感悟三种思路模型中的内在联系与区别。在比较反思中验证模型时,可以通过思维导图来比较思路模型的异同,帮助学生进一步感悟、理解数学模型,积累模型经验。

如在探究时,如果只出示题目,就让学生列式解答,不符合二年級学生以直观形象思维为主的特点。因此,可以设计从原来条件中依次选择条件进行重组,然后用箭头图的形式展示出来,并把先选用的2个条件框出来,突出可以先算什么。这样,在学生叙述的基础上,把他们的思维过程通过操作直观呈现出来,有助于理出三种思路模型,有助于在较反思中抓住两步计算实际问题的数学模型思想。
正所谓,“知其然,更要知其所以然”。在经历数学建模的过程后,要注重比较反思,结合具体的生活情境,来解释验证数学模型。在本节课中,基于生活经验,一般先上后下,符合学生的逻辑顺序,这是生活模型的一种数学运用;也可以采用先上后下的逆向思维,这种思维超越了生活经验,是源于生活又高于生活的体现;还可以利用数量之间的关系建立数学模型,先求出上车比下车多的人数,再和原来的人数相比较,在比较反思中促进理解,这是建模的灵魂。
四、实践应用,巩固模型——建模的延展
在学习新的数学模型后,要引导学生及时运用所学知识来解决生活中的一些实际问题,进一步巩固数学模型,体验数学模型的应用价值,提高解决问题的能力。因此,练习的设计形式要多样,要凸显两步计算的实际问题的延展,在练习中逐步帮助学生形成具有可操作性的解决两步计算实际问题的数学模型,将学生已有的知识、经验、方法融为一体,丰富解决问题的方法、途径、手段。
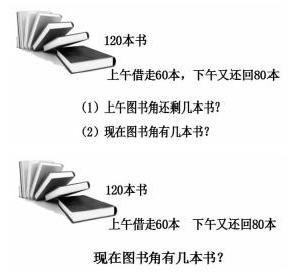
如在练习时,可以精心设计习题的呈现形式,关注前后知识间的联系与区别,注重在比较中把握两步计算的解决问题的一般方法。
1.箭头图
可以把例題和这题联系起来比一比,例题中是2次变化后比原来多了3人,所以要用原来的人数加3人,就是离站时车上的人数;而试一试中是2次变化后比原来少了2包,所以要用原来的包数减2包,就是还剩的包数。这题是例题的延续,通过比较这两题,可以进一步完善解决两步计算的实际问题的一般模型。
2.直条图
为学生创设插花情境,让学生根据条件来提问题并能灵活地解决。通过这样的形式,让学生进行直观地比较,明确要根据问题的不同特点,要选择合适的条件来解决,理解和掌握其中蕴含的一步计算应用题的数学模型与两步计算应用题的数学模型的内在联系。
3.图文结合
针对书上的西瓜问题,可以巧妙地进行修改设计,加强单元整体的教学。通过比较发现左边一题是以前学的连续两问的实际问题,右边一题是今天学的两步计算的实际问题,而且两步计算中的第一步求的就是连续两问中的第一个问题。在比较练习中,进一步帮助学生理解和理清连续两问应用题的数学模型与两步计算应用题的数学模型的内在联系。
4.表格。
书上的表格题直接呈现了包含两个小问题的一个大问题,对于二年级的学生来说,理解和解决起来都难度较大。为此,可以进行修改设计,先解决小西提出的问题“我们班不会打棒球的有多少人?”,再让学生自己提问并解决“我们班不会打篮球的有多少人?”。在此基础上,以变魔术的形式,让学生直观感受,两个小问题是如何合并成一个大问题的,从而理解在更复杂的两步计算应用题中如何运用数学模型。

在探究和学习力初步的数学模型思想后,要引导学生把所学的数学模型推广运用到生活中的一些情境中去,在巩固的过程中进一步理解数学模型。在练习中,这样的练习设计凸显了两步计算实际问题的应用和延展,通过应用让学生真正走入生活,掌握两步计算实际问题蕴含的数学模型,培养学生的应用意识、创新意识、实践意识,逐步完善解决问题的数学模型的体系,这是建模的延展。
随着新课程的改革,数学模型思想越来越成为课堂教学的指导理念,同时也是知识与生活的沟通桥梁。因此,要聚焦数学模型思想,精心设计课堂教学,从以下几个方面入手:创设情境,感知模型——叙述思路,建立模型——比较反思,验证模型——实践应用,巩固模型。在解决问题的教学中渗透模型思想时,要关注建模的起点、建模的关键、建模的灵魂、建模的延展,这些都有助于学生更好地掌握数学模型思想,进一步提高学习数学的兴趣和应用模型思想的意识。
【参考文献】
[1] 冼鉴民,新课程学习[J]. 利用数学模型,搭建学生学习的脚手架,2013.
[2] 陈建和,新教育时代电子杂志(学生版)[J].关于小学数学教学中渗透模型思想的思考,2016.
[3] 张春莉,小学教学[J].数学模型思想与小学数学教学,2016.
[4] 国彩霞,读写算(教研版)[J].如何在教学中渗透数学模型思想,2015.
[5] 莫杰益,小学科学(教师版) [J].小学数学教学如何培养学生的模型思想,2017.

