感知旋转方法，感悟模型应用

薛琼

[摘  要] 图形旋转是三大几何变换之一，图形旋转的过程中蕴含着众多的数学规律，以图形旋转为依托构建的解题方法是数学几何重要的方法之一，文章将以一道典型问题为例，提炼旋转模型，探究旋转法的解题应用，提出相应的教学思考，与读者探讨.

[关键词] 几何;图形旋转;旋转法;线段长;模型

典型问题的解答

题目  图1所示的四边形ABCD中，AE⊥BC，∠BAE=∠ADC，BE=CE=2，CD=5，AD=kAB （k为常数），则BD的长为______（用k表示）.

解答  连接AC，由于BE=CE，AE⊥BC，故△ABC为等腰三角形，即AB=AC（等腰三角形三線合一）. 由∠ABE+∠BAE=90°，∠BAE=∠ADC，可得∠ABE+∠ADC=90°. 将△ACD绕点A顺时针旋转至点C与点B相重合，再连接DF，如图2所示，进而可证△ADC≌△AFB，由全等性质得∠AFB=∠ADC，BF=CD，∠BAC=∠DAF，进一步可证△FAD∽△BAC，所以∠AFD=∠ABC，∠BFD=90°. 由AD=kAB可得DF=kBC=4k，在Rt△BDF中由勾股定理可得BD2=BF2+DF2，因此BD=.

解题模型的提炼

上述考题在求解过程中采用了图形旋转的方式，将△ACD绕点A顺时针旋转了一定的角度，使得AC与AB边相重合，使两个不相邻的角结合在一起，且获得Rt△BFD，其中的直角∠BFD在整个解题中起着重要的作用，是构建代数方程的关键. 上述解题过程利用到了几何内容最为重要的一种模型——旋转模型，旋转模型对于构建等角、等边、图形相似与全等有着重要的意义，而这些条件是后续解题突破的基础，下面将深入探析几何的旋转模型.

旋转模型用到的基本理论是几何旋转的性质，在图形旋转过程中图形的形状不变、图形全等、对应边、对应角相等，且对应点到旋转中心的距离相等，边的旋转角度也相等.

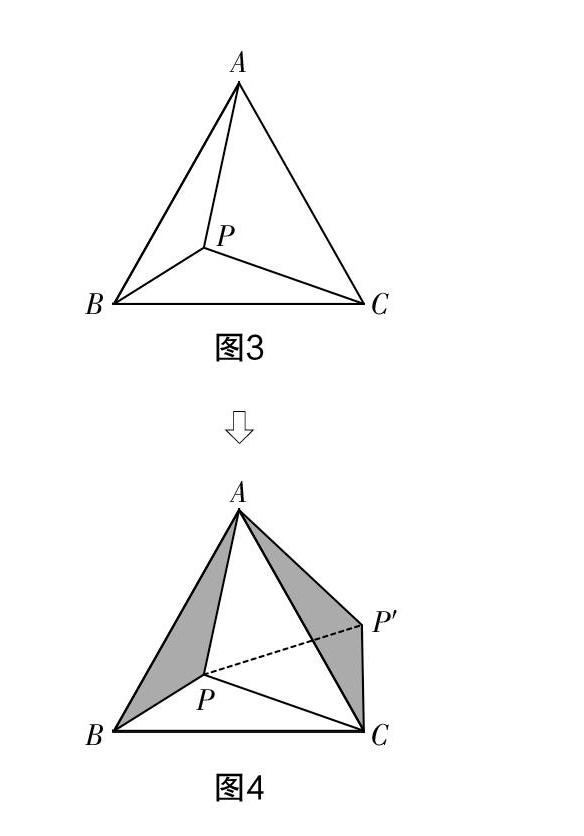
上述考题是关于基本三角形的旋转，以图3所示的△ABC为例，在图形旋转过程中必须明确旋转的三要素——旋转中心、旋转方向和旋转角度. 在等边三角形ABC的内部存在一点P，将△ABP绕点A逆时针旋转∠BAC，则AB将与AC相重合，AP=AP′，AB=AC，BP=CP′，∠BAP=∠CAP′，∠ABP=∠ACP′，∠APB=∠AP′C，△ABP≌△ACP′，即两个阴影图形全等，对应边和角均相等. 图形旋转后获得了新的四边形ABCP′，在该复合图形中有一个特殊的等边三角形△APP′（AP=AP′=PP′），出现了多个复合角：∠BCP′，∠BAP′，∠PCP′和∠PAP′，这些新出现的几何元素可以成为问题解答的关键条件.

旋转模型的应用

几何旋转法是为了解决特定的问题，考虑到旋转过程变化的对象较多，构建的新模型具有多种特征，因此在使用时必须明确旋转图形的目的，通过旋转可以构建怎样的图形，解决哪些问题.

通过上述旋转模型的分析我们可以发现构建了复合角，实际上是将两个不相邻的角紧密地联系起来，同时也可以将不共线的线段转换在同一直线上，即实现角度的“互补”、线段的“互补”. 第二种用途则是构建特殊的图形和几何关系，如等边、等腰三角形和全等、相似三角形，因此图形的旋转过程实际上就是线段、角度、图形重构的过程，旋转模型最为普遍的用途是求解线段长、几何角度和分析图形形状. 利用旋转法进行解题时可以遵循如下思路：判断是否旋转→确定旋转三要素→分析旋转重构条件→重组问题条件→构建解题思路，从而将原始条件与旋转性质条件充分结合起来，为后续的解题突破提供帮助. 下面结合一道考题深入讲解旋转模型的利用.

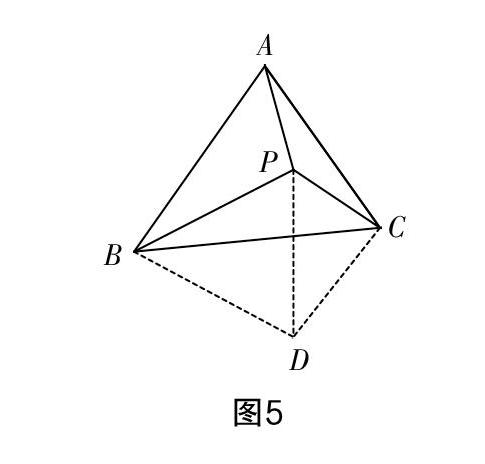
例1  图5所示等边△ABC的内部有一点P，已知∠APB，∠BPC和∠CPA的大小之比为5 ∶ 6 ∶ 7，则以线段长PA，PB和PC三边组成的三角形的内角大小之比为________（由小到大）.

分析：

第一步：判断是否旋转.

由问题出发进行分析，要求解△ABC内部三条线段所构三角形的内角之比，考虑到三条线段没有形成闭合图形，显然需要通过旋转的方式将其连接成三角形.

第二步：确定旋转三要素.

将△ABP以点B为旋转中心，顺时针旋转60°得到了△CBD，连接PD，如图5所示.

第三步：分析旋转重构条件.

由于△ABP通过旋转得到了△CBD，旋转前后AB=BC，BP=BD，AP=CD，∠BDC=∠BPA.

第四步：重组问题条件.

结合∠BPD=60°可得△PBD为等边三角形，有PD=PB，则以线段PC，PD和CD为三边的△PCD就是题干要求组成的三角形，求三角形内角大小之比就是求∠PDC，∠CPD和∠PCD的大小之比.

第五步：构建解题思路.

根据条件“∠APB，∠BPC和∠CPA的大小之比为5 ∶ 6 ∶ 7”可得∠APB=100°，∠BOC=120°，∠CPA=140°，则∠PDC=∠BDC-∠BDP=40°，∠CPD=∠BPC-∠BPD=60°，进而求得∠PCD=80°，所以∠PDC，∠CPD和∠PCD的大小之比为2 ∶ 3 ∶ 4，即以PA，PB和PC三边组成的三角形的内角大小之比为2 ∶ 3 ∶ 4.

旋转模型的拓展

从上述考题的分析可知旋转模型可以用于三角形类型题中的边长和角度分析，对于其他多边形我们也可以采用旋转的方式来构建解题模型，求解一些较为特殊的问题，如求解面积、关系式证明等. 下面我们以正方形题型为例进一步探究旋转模型的应用.

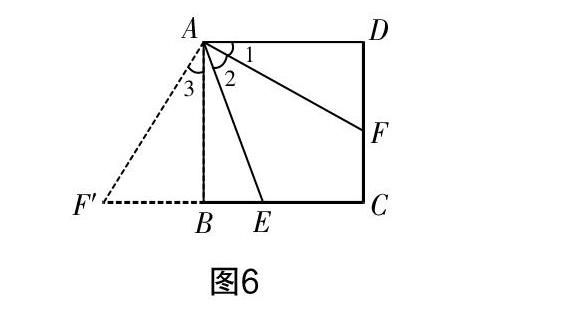
例2  四边形ABCD为正方形，点E是BC边上的一点，AF平分∠EAD与CD相交于点F，试证明AE=BE+DF.

解析  求证AE=BE+DF，考虑到三条线段长分散在不同的三角形中，无法直接构建线段长关系，可以采用图形旋转的方式将其转化到同一三角形中. 现将△ADF绕点A顺时针旋转90°，如图6，则点D将与点B重合，而点F移动到F′的位置. 根据旋转模型的性质可得△ADF≌△ABF′，进一步可知∠AFD=∠AF′B，∠3=∠1，DF=F′B，则BE+DF=F′B+BE=F′E，只需要证明F′E与AE相等即可.

由圖6可知∠1+∠ABE+∠2=90°，因∠3=∠1，故∠3+∠ABE+∠2=90°=∠F′AE+∠2，又知∠AF′B+∠3=90°，结合∠1=∠2=∠3，可得∠AF′B+∠2=90°，即∠F′AE=∠AF′B，由等角对等边可得F′E=AE，得证.

上述考题揭示了使用旋转法最为关键的一点，即将不共线的线段转移到同一直线上，进而将旋转模型的应用拓展到多边形中，不再局限于传统的三角形，只需遵循图形旋转的三要素即可. 另外对于旋转模型性质的利用可以从以下两个方面来理解：一是传统意义上的旋转前后图形对应元素相等，二是从图形全等的角度，旋转前后的两个图形满足全等的条件，由图形全等的性质同样可以获得诸多旋转性质. 因此可以将旋转模型法拓展到所有的几何图形中，不受题型和旋转图形的限制.

方法教学的思考

1. 形成旋转模型使用的逻辑思维

数学的解题方式有很多，考虑到图形旋转过程中发生位移变化的对象较多，因此使用该方法进行解题需要严格遵守使用原则. 首先要根据题干的条件和问题来判断是否可以采用旋转模型，然后遵循旋转要素进行合理旋转，并根据旋转模型的性质挖掘隐含条件从而完成解题条件的重组，最后充分利用重组条件开展解题突破. 因此进行几何旋转法教学实践时可以按照“方法判断→实施旋转→条件挖掘→重组条件→构建思路”的步骤进行，使学生形成旋转法解题思路的深刻记忆.

2. 形成几何旋转法的本质认识

图形旋转前后所获得的是全等图形，因此可以说利用图形旋转来解题实际上是对全等性质的拓展运用，旋转法与图形的全等和相似之间有着紧密的联系，这也是教材将两大内容编排在一起的根本原因. 在教学图形旋转法时就需要引导学生重温几何全等的性质，以及图形旋转过程中“变”与“不变”的性质，从全等和不变性两个角度引导学生进行旋转法的探索学习，充分理解该方法的理论依据，认识旋转模型的性质本质，从而深刻认识该方法的数学内涵.

3. 形成几何旋转模型的思想认识

数学的解题方法都具有一定的理论思想，是在对应数学思想的指导下构建的解题方法，对于几何旋转法同样不例外. 几何图形旋转过后会得到一个全新的图形，因此图形旋转的过程实际上就是数学建模的过程，图形旋转就是在数学模型思想指导下完成的. 在方法教学中不能单纯地向学生传达方法的使用步骤，还应该依托具体的教学内容渗透数学的模型思想，使学生体会使用数学模型解决实际问题的优势. 可以借助几何画板完成旋转模型的构建，使学生充分参与模型思想方法的辨析讨论，提升动手能力的同时获得数学思想的提升.

结束语

从图形旋转法的本质内容来看，该方法属于“空间与图形”的教学范畴，因此在该方法的教学中需要遵从“观察感知、动手实践、内涵理解”的理念，即教学中要使学生掌握该方法的使用依据、具体操作和思想内涵. 图形旋转的过程蕴含着数学特有的美感，因此依托考题开展方法教学，不仅可以使学生体会数学方法的解题魅力，还可以激发学生学习数学的兴趣，充分调动学生的数学思维，后者对于学生的发展具有深远的意义.