基于变式 构造模型
——“圆的拓展应用”课堂实录与评析
陈世文,时爱荣
(浙江师范大学附属嘉善实验学校;浙江省嘉兴市教育学院)
2017年11月24日,笔者在浙江省名师课堂展示暨嘉善县第五届课博会上成功开设“圆的拓展应用”展示课,课堂从一个基本模型出发,通过变式题组推进,让学生逐步感悟并掌握解题的思想方法,最后通过拓展提高,将学生的思维进一步升华.整节课衔接自然、流畅,题目设计精巧、有梯度,注重学生思维的提升和能力的培养.受到与会教师的一致好评,现将本节课的实录与点评呈现如下,期待与同行分享、交流.
一、课堂实录
1.提炼模型
师:在之前的学习中,我们经常会遇到求最值的问题,大家回顾一下,求最值常用到哪些知识与方法?
生1:利用两点之间线段最短求最值.
生2:利用三角形两边之和大于第三边,两边之差小于第三边求最值.
生3:建立二次函数模型,利用二次函数求最值.
……
师:非常好!看样子大家对求最值已经有了一定的经验积累,本节课我们就来学习利用辅助圆求最值.
题目1如图1,⊙O的半径r=2,P为⊙O外一点,且OP=5,A为⊙O上一动点,求PA的最大值和最小值.
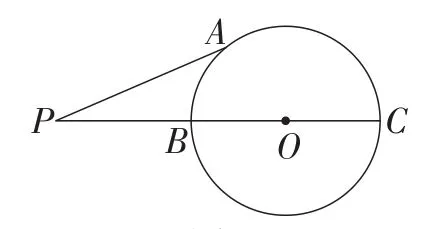
图1
生4:当点A位于点B时,PA最小,最小值为3;当点A位于点C时,PC最大,最大值为7.
师:能说一下理由吗?
生5:如图2,连接OA,当点A与点B,C不重合时,根据三角形两边之和大于第三边,两边之差小于第三边,可得PO-OA<PA<PO+OA,即PB<PA<PC.所以当点A位于点B时,PA最小,当点A位于点C时,PA最大.
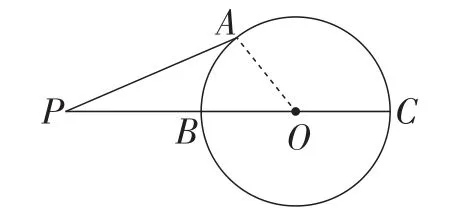
图2
【评析】利用学生熟知的、简单的问题,激活学生的思维与已有认知,提炼出圆外一点到圆上动点距离的最值几何模型,为后续学习做好准备.
2.应用模型
题目2如图3,在Rt△ABC中,∠B=90°,AB=6,BC=4,以AB为直径的半圆交AC于点D,P是上的一个动点,连接CP,则CP的最小值是多少?
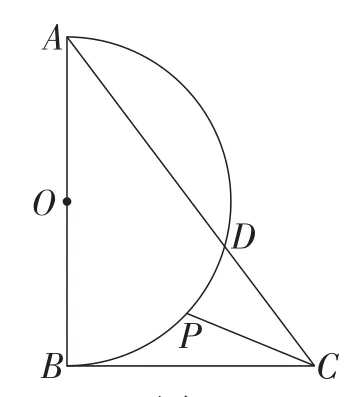
图3
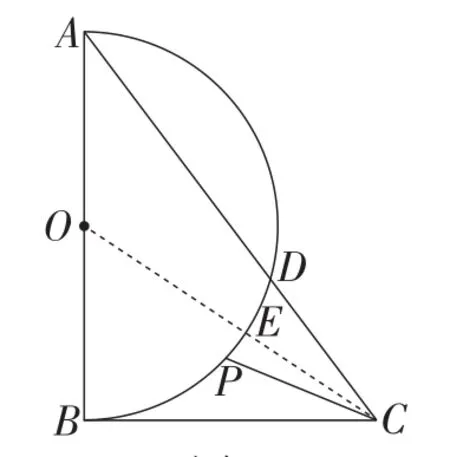
图4
生6:如图4,连接OC与⊙O相交于点E,由刚才的模型可知当点P运动到交点E时,CP取得最小值,最小值为5-3=2.
【评析】在最近发展区内,以基本模型为固着点,设计一个低起点问题,及时运用、巩固基本模型,强化学生的模型思想与意识.
变式1:如图5,在Rt△ABC中,∠B=90°,AB=6,BC=4,D是AB的中点,E是线段BC上的动点,将△BDE沿DE所在的直线折叠得到△B′DE,连接B′C,则B′C的最小值是多少?
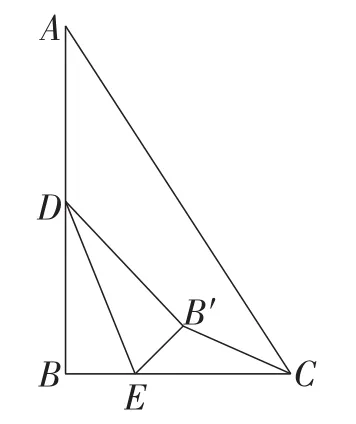
图5
生7:如图6,点B′在以点D为圆心,BD长为半径的圆上,连接CD,当点B′位于CD与⊙D的交点时,B′C取得最小值,且最小值为2.
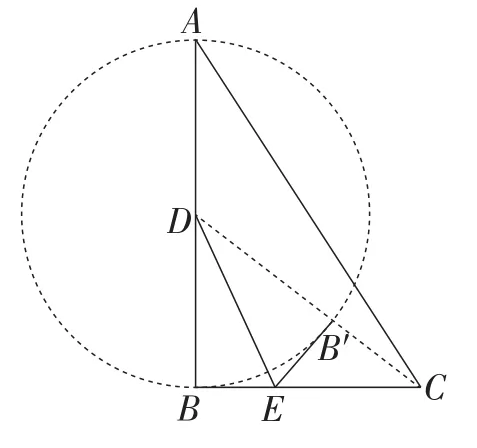
图6
师:点B′为什么在以点D为圆心,BD长为半径的圆上?
生8:因为B′D=BD=3,到定点的距离等于定长,所以点B′在以点D为圆心,BD长为半径的圆上.
师:非常好!由此可见,大家觉得求CP最小值的关键是什么?
生9:关键是确定动点B′的运动路线,若其运动路线是圆,则将问题转化为圆外一点到圆上动点距离的最值模型.
【评析】通过变式1,让学生感悟、体会解决此类最值问题的关键是确定动点的运动路线,若其运动路线是圆,则将问题转化成圆外一点到圆上动点距离的最值模型.而确定动点的运动路线主要根据圆的定义.
变式2:如图7,在Rt△ABC中,∠B=90°,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP长的最小值是多少?
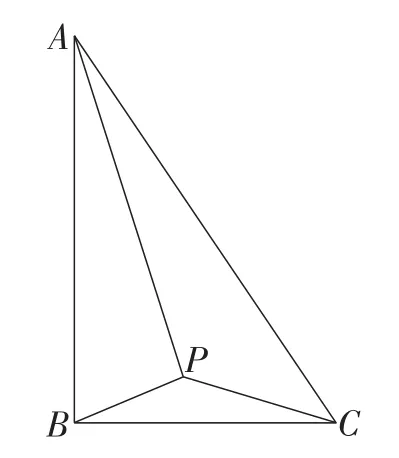
图7
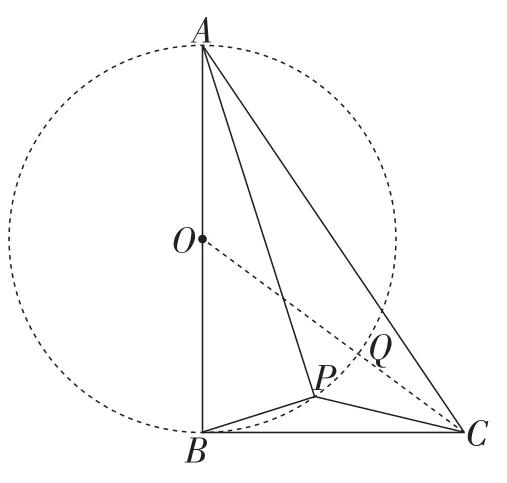
图8
生10:如图8,点P是在以AB为直径的圆上运动,设AB的中点为点O,连接CO与⊙O相交于点Q,则当点P位于交点Q时,CP取得最小值,且最小值为2.
师:非常好!此时点P为什么在以AB为直径的圆上运动呢?
生11:因为 ∠PAB=∠PBC,∠PBC+∠PBA=90°,所以 ∠PAB+∠PBA=90°.所以 ∠APB=90°.根据直角三角形斜边的中线等于斜边的一半,可知点P到AB的中点的距离始终等于,所以点P在以AB为直径的圆上运动.
师:还有其他方法可以确定点P在以AB为直径的圆上运动吗?
生12:∠APB=90°,根据直径所对的圆周角是直角,可知点P在以AB为直径的圆上运动.
【评析】通过变式2,从不同的视角来探求确定圆的条件,让学生感悟、体会确定运动路线的方法除了定义外,还可以根据圆的性质——直径所对的圆周角是直角.同时起到承上启下的作用,为变式3做好思维的铺垫.
变式3:如图9,在等边三角形ABC中,,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP长的最小值是多少?
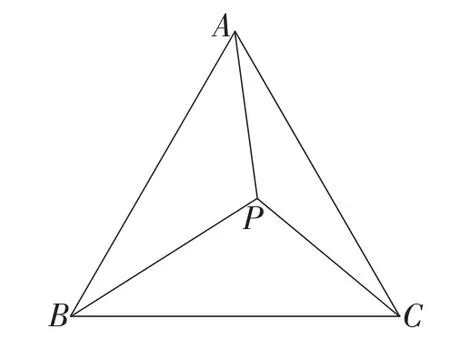
图9
生13:因为∠PAB=∠PBC,∠PBC+∠PBA=60°,所以∠PAB+∠PBA=60°.所以∠APB=120°.所以点P的运动路线也是圆.
师:为什么呢?
生14:因为同弧所对的圆周角相等,所以∠APB应该是圆周角.所以点P的运动路线也是圆.
师:非常好,这样只要画出点P的运动路线(圆),就可以将其转化成圆外一点到圆上动点距离的最值模型了.
师:最后大家总结一下,通过这三道变式,你觉得确定动点的运动路线(圆),主要有哪些方法?
生15:根据圆的定义和同弧所对的圆周角相等.
【评析】变式3是变式2的拓展与一般化,让学生进一步感悟、体会确定运动路线的方法:只要当一条线段所对的张角是定值时(并不要求一定是直角),角的顶点运动路线就是圆.同时通过教师的追问,及时总结、归纳出确定动点运动路线的方法.
3.拓展提高
题目3如图10,边长为的等边三角形ABC的顶点A在x轴的正半轴上移动,顶点B在y轴的正半轴上移动,求顶点C到原点O的最大距离.
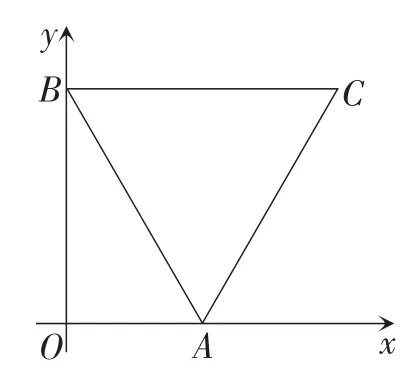
图10
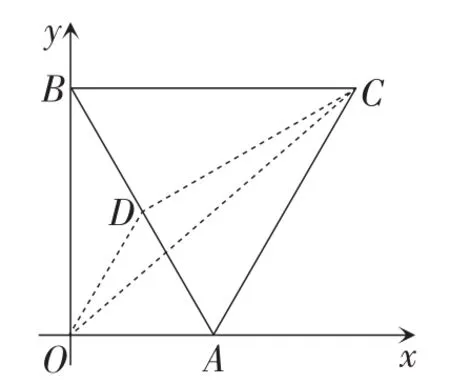
图11
生16:如图11,取AB的中点D,连接OD,CD,OC,则.所以顶点C到原点O的最大距离是.
师:能否将其转化为圆外一点到圆上动点距离的最值模型?
生17:我发现点C的运动路线不是圆,所以不能运用刚才的模型.
师:我们知道相对运动,点C的运动路线不是圆,那么能否将点C固定,只让点O运动呢?
生18:可以,将△ABC固定,点O运动,因为∠AOB=90°,所以点O的运动路线是以AB为直径的圆.
师:非常好,这样就转化成了圆外一定点到圆上动点距离的最值了,接下来大家自己完成.这种解决问题的方法我们称为“动静互化”.
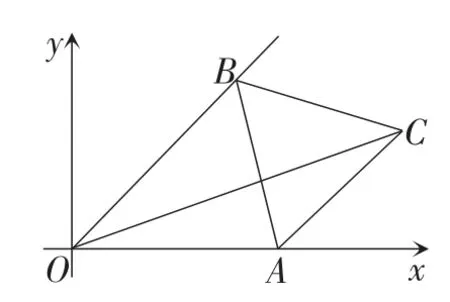
图12
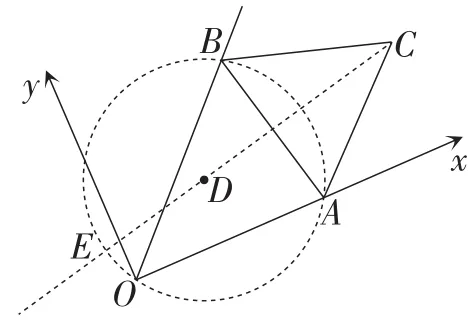
图13
生19:假设△ABC不动,点O运动,由于AB固定,∠AOB=45°,所以点O的运动路线是圆.如图13,作△ABO的外接圆⊙D,连接CD并延长,交⊙D于点E,则当点O运动到点E时,CO取得最大值.
师:非常好!生19运用动静互化,确定出点O的运动路线,从而将这道题目转化成了圆外一点到圆上动点距离的最值模型.
【评析】从单点运动到多点运动,给学生造成思维的障碍,引发认知冲突,从而自然引出动静互化的解题方法.
4.巩固练习
练习:如图14,已知∠MON=30°,矩形ABCD的顶点A在OM上运动,顶点B在ON上运动,且AB=2,BC=1,求点C到点O的最大距离.
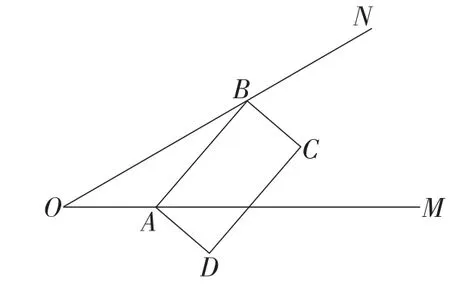
图14
【设计意图】将直角坐标系的背景去掉,同时将45°角变为30°角,难度进一步加大,深刻考查学生对动静互化和定弦、定角确定运动路线(圆)方法的理解和掌握情况.
二、课堂点评
1.基于变式,知识自然生长
本节课利用题目1,让学生在运用“三角形两边之和大于第三边”“三角形两边之差小于第三边”等知识来分析、解决问题的过程中提炼出“圆外一点到圆上动点距离的最值”模型,再通过题目2、题目3,及其变式题组,一步一个台阶,层层推进,让学生不断经历构造几何模型、运用几何模型来分析问题和解决问题的过程,在这个过程中学生逐步掌握了构造模型和动静互化的方法,体会了转化思想和数形结合思想.
这种从最简单处入手,逐渐变式生长,不断拓展深化的教学设计,形式简洁、立意高远、清新自然.充分调动了学生的学习热情、学习主动性和积极性;培养了学生灵活、深刻、广阔、发散的数学思维能力,以及大胆创新、勇于探索的精神,从而真正把学生能力的培养落到实处.
2.构造模型,渗透数学方法
在学习平面几何的过程中,学生经常会遇到无法直接解答的难题.这时,构造辅助图形对于解题就显得非常重要,而大部分学生在解答平面几何问题时,常常会“想当然”的作出错误的辅助线,或是不知道从何下手.因此,教师要引导他们明确如何构造辅助图形,合理的构造辅助图形在解题过程中一般起着某种桥梁作用,将已知条件和求证结合起来,形成一条逻辑证明的思维通道,能使所求问题得到更好的解决,在这个过程中,重要的是掌握思想方法,学会如何构造.
本课例中构造辅助圆(即动点的运动路线),将问题转化成基本模型是解题的关键,教师通过题目2的三道变式让学生逐步感悟、总结、归纳出确定运动路线——辅助圆的方法:(1)到定点的距离等于定长;(2)定线段、定角度.在这个过程中学生掌握了解决动态问题的本质方法——抓住变中不变的量.例如,线段长度不变、角度大小不变.同时体会、领悟了数学中构造、转化的方法,积累了数学知识和活动经验,提升了解题能力.
3.问题驱动,引发深度思考
问题驱动是指学生在问题的启发下进行独立思考、发展思维的探究性学习.问题驱动下的数学教学是用数学问题组织教学,通过问题驱动学生学习数学知识.苏格拉底认为,教学生不是直接教给学生知识,而是将原本存在在学生心灵深处的知识引导出来;问答式教学应该教学生认识真理的方法,而不是直接将现成的真理教给学生,教师在引导学生认识真理的过程中起助产的作用.
本课中,教师以“问”为导向,层层设问.用“问”让学生理清思路;用“问”来追溯本源;用“问”来引领学生深入思考;用“问”来引导学生及时归纳概括.
这种问题驱动的学习模式不以教学为中心,而是以问题为中心,通过对问题的回答反映学生的学习成效,引发学生的深度思考.在学生学习的各个阶段,学习过程必须基于已学知识,以及学科知识的学习或学习框架的构建,将学生的思维能力、解决问题的能力,以及掌握学习方法的能力加以提高,促进了学生自主学习的能力,从而提升学生的数学核心素养.

