初中数学解题后的反思策略探究
沈晓生
(福建省诏安县怀恩中学)
在初中数学教学中常存在这样一个现象:多数学生做数学题时想方设法去解题,但解题后没有进行归纳总结,也就是没有把解题前的探索与解题后的反思紧密地结合起来,达不到提高解题能力的理想效果.事实上,就优化数学解题思维、提高解题能力的重要性而言,解题后的反思不亚于解题前的探索.因为解题后的反思过程是学生自觉地对自身活动进行回顾、思考、总结、评价和调节的过程.下面,笔者就如何引导学生进行解题后反思谈几点建议.
一、反思审题,是否弄清楚问题的特征
解决问题要找准突破口,而抓住了问题的主要特征也就打开了突破口.数学题目往往具有某种特征,它是正确解题的重要因素.在审题时,只有充分挖掘、分析、理解题目的特征,明确条件和目标,才能快速形成正确的解题思路.在教学中,教师要启发学生在解题后全面观察、综合分析问题的主要特征,弄清楚已知条件告诉了我们什么,目标要求什么,如何从中寻找解决问题的关键,最终获取最佳方法,正确解答.
解题时能否弄清楚题目的特征,重点是对题目给出的条件的分析是否到位.如果对条件和结论的理解认识不全面,特别是对题目中的条件(尤其是隐含条件)考虑不周全,那么就会导致错解.
例1若实数m,n满足,且m,n恰好是等腰三角形ABC的两条边的边长,则△ABC的周长是( ).
(A)12 (B)10 (C)8 (D)6
解析:根据绝对值和二次根式的非负性,得m-2=0,n-4=0.解得m=2,n=4.再根据m,n是等腰三角形ABC的两条边的边长,分情况讨论:①若腰为2,底为4,由三角形两边之和大于第三边,可知此时不能构成三角形,舍去;②若腰为4,底为2,周长为10.故选B.
此题是求等腰三角形的周长,它的主要特征是要确定能形成等腰三角形的腰和底的长,因此当腰和底不明确时则需要进行讨论.像这类题目,只要抓住已知条件的特征进行理解、辨析,就能达到“见题有法,逢题获解”的功效.
因此,教师应引导学生认真对待解题后的反思,对题目条件、结论进行再认识,特别是对条件与结论之间存在的数量关系或位置关系等特征进行分析,检查逻辑推理是否科学,思考是否抓住了问题的本质.
二、对解题思路进行反思
解题思路的反思重点可以从三个方面进行:(1)是否理解题意并提取有用的信息,如数式特点,图形结构特征等;(2)能否从已有知识中提取出相关的信息,如有关的公式、定理、基本模型等;(3)能否将上述两组信息进行有效整合重组,生成一个合乎逻辑的解题思路.
例2已知:m2-2m-1=0,n2+2n-1=0,且mn≠1,则的值为_______.
解析:此题中,观察两个方程中系数符号的异同是关键.将n2+2n-1=0变形,即1-2n-n2=0.进而变形为.对照第一个方程可判断其结构相似,据此可得m,是方程x2-2x-1=0的两个根.由根与系数的关系,可得.代入原式,得.
对于这类题目,学生往往会在解题过程中,只用概念或公式、法则、定理中的某个条件进行解题,导致解题错误.因此,解题时必须对相关条件的相似情况或异同点加以关注,对重要信息进行分析,结合方程、不等式、函数基本模型进行求解,周密思考问题的本质,形成正确的解题思路.
三、对解题方法进行反思
教师可以给学生提供多渠道的思考方式,运用一题多解、一题多变、直观思维(形)与抽象思维(数)相互转化的方法,引导和启发学生,让学生进行反思,力求解中求多、多中求妙,有效促进学生养成良好的学习方法,培养学生灵活运用知识的能力.
1.一题多解,培养学生的发散思维
例3如图1,在△ABC中,D是AB上任意一点,在AC的延长线上取一点E,使CE=BD,连接DE交BC于点F.求证:FD∶FE=AC∶AB.
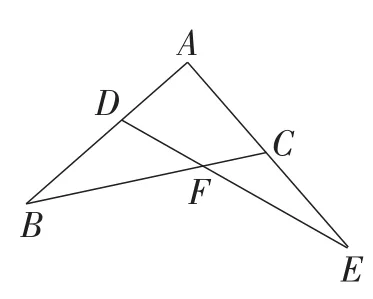
图1
解法1:如图2,过点D作DG∥BC,交AC于点G,则.
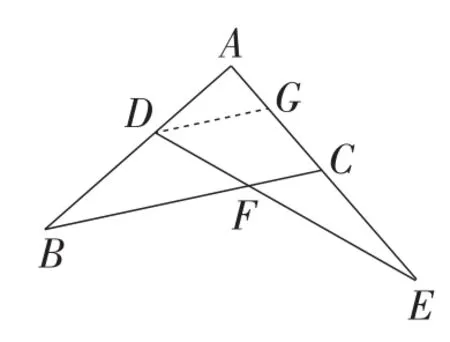
图2
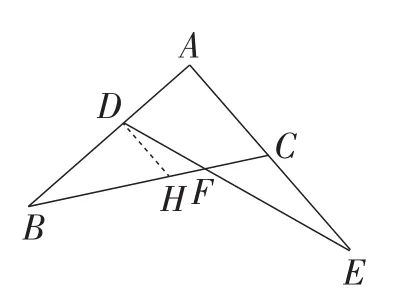
图3
解法2:如图3,过点D作DH∥AC,交BC于点H,则.
解法3:如图4,过点E作EK∥CB,交AB的延长线于点K,则.
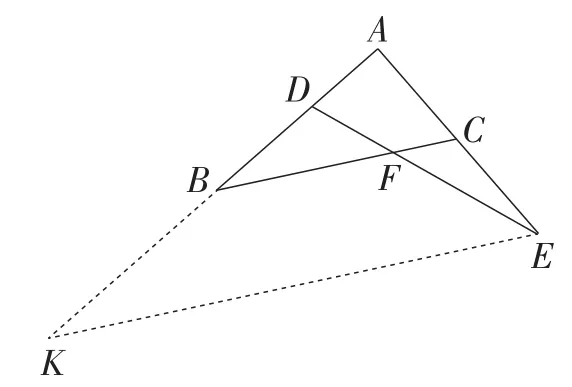
图4
解法4:如图5,过点E作EM∥BA,交BC的延长线于点M,则.
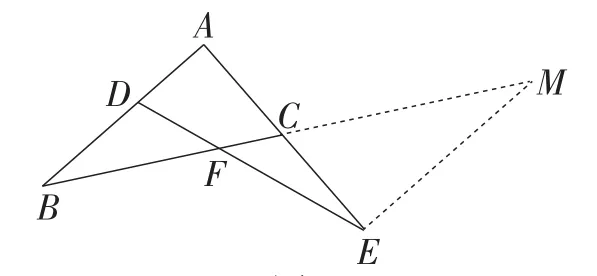
图5
证明此题的关键在于判断比例式中的线段是否在同一直线上,若是,则可以从线段的端点引平行线,获得所需的比例式,因此可有多种解法.
一题多解重在对学生进行多向思维训练,贵在化繁为简,择优解法.利用一题多解引导学生从不同方面,运用不同途径去解决同一类题,既可以巩固已有知识,又能拓宽解题思路.
2.一题多变,培养学生的变通性
例4如图6,已知a∥b,c∥d,∠1=115°.
(1)求∠2与∠3的度数;
(2)你能得到∠1与∠2之间是什么关系?
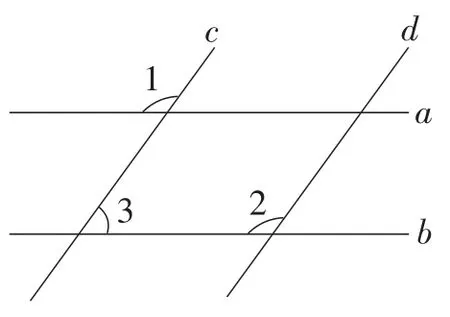
图6
此题通过平行线的性质求解角的度数及角与角之间的关系,熟悉平行线的性质是解题的关键.
在师生共同解答后,笔者将题目改为:如图6,已知:a∥b,c∥d,求证:∠1=∠2.笔者让学生写出证明过程,并说出各自不同的证法.由于与此题紧密相关的内容是平行线的判定,因此又可以有如下变化.
变式1:如图6,已知a∥b,∠1=∠2,求证:c∥d.
变式2:如图6,已知c∥d,∠1=∠2,求证:a∥b.
变式3:如图6,已知a∥b,问∠1=∠2吗?
通过对题目的条件或结论进行合理的变化,把原题加以变形、延伸,进行从一个问题到一类问题的变式训练,灵活运用所学的知识解决问题,促进学生对基础知识的巩固,培养学生的发散思维和创新能力,达到发展数学能力的目的.
3.对直观思维(形)与抽象思维(数)相互转化的反思,培养数形结合思想
解数学问题离不开直觉,在推理中需要直观能力的帮助,这是因为证明所用的逻辑材料很多,需要通过直觉选择这些材料构成数学建模.有些数学问题可以利用画图来解决,它能化隐性条件为显性条件,启发直观思维.有些代数问题条件中的数量关系具有明显的几何意义,或用某种方法可以与几何图形建立联系.因此,若能将已知条件中的数量关系寓于特定的几何图形中,则能快速地找到解题途径.所以,数形结合就是根据问题实际由数思形,以形助数,适时转化,相互作用.因此,在教学中,教师应该有意识地引导学生学习这种转化方法.
(1)利用图形解数学题.
例5如图7,在物理课上,老师将挂在弹簧测力计下端的铁块浸没于水中,然后缓慢匀速向上提起,直至铁块完全露出水面一定高度,则能反映弹簧测力计的读数y(单位:N)与铁块被提起的高度x(单位:cm)之间的函数关系的大致图象是( ).
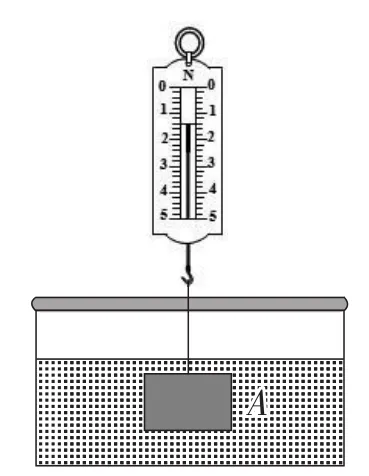
图7
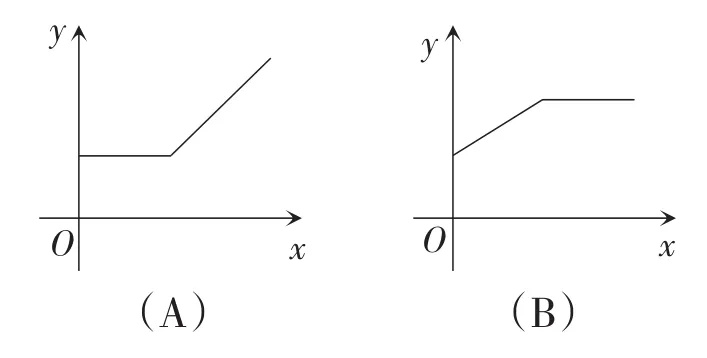
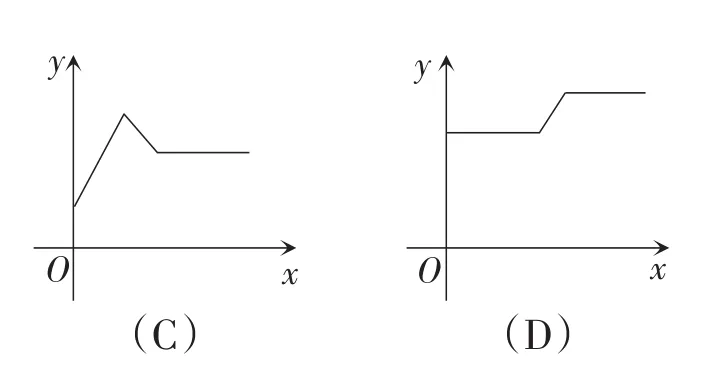
解析:根据题意,铁块露出水面以前,浮力不变,故此过程中弹簧测力计的度数不变.当铁块开始慢慢露出水面时,浮力逐渐减小,则拉力逐渐增加,当铁块完全露出水面后,拉力等于重力.故选D.
图象信息题既能考查学生的运算能力、抽象能力、空间观念和应用意识,也能体现数形结合思想.解题时,首先,要熟悉已学的几种常用的函数图象性质,即正比例函数、一次函数、二次函数和反比例函数;其次,要求学生能根据具体的问题情境,抓住问题中的变量,变量与图中的数据的对应关系,明确它们的几何意义,再根据图象的特点,用数形结合的方法求解.
(2)几何题的代数解法.
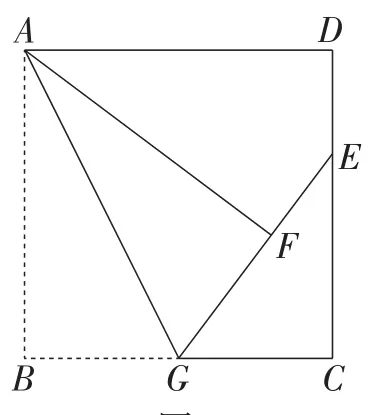
图8
例6如图8,正方形ABCD中,AB=6,G是BC的中点.将△ABG沿AG对折至△AFG,延长GF交DC于点E,则DE的长是( ).
(A)1 (B)1.5
(C)2 (D)2.5
解析:根据翻折变换的性质和正方形的性质可得Rt△AFE≌Rt△ADE.所以EF=DE.设DE=FE=x,则EC=6-x.因为G为BC的中点,BC=6,所以CG=3.在Rt△ECG中,根据勾股定理,得(6 -x)2+9=(x+3)2.解得x=2.故选C.
几何题一般采用逻辑推理来求解,但在有些情况下,用代数方法解更为简捷.从例6可以看出,用代数方法解几何题的一般思路是,对于有提供边角关系、直角三角形、折叠对称等求数量关系的类型,可以通过分析已知条件各元素之间的数量关系和图形的几何特征,运用有关定理和公式建立数量关系,然后借助代数方法求解.
总之,解题反思就是解题后围绕审题、解题思路、解题方法等,展开多角度、多层次的反思,而不是简单的回顾.科学的解题反思是提高学生解题能力的有效方式.

