曲线约束摩擦力速度问题的求解

何 健

(绵阳师范学院数理学院，四川 绵阳 621000)

利用自然坐标系处理含约束的质点动力学问题是大学物理中常见的类型。此类问题通常配合使用双坐标形式，以自然坐标系描写力，直角坐标系描写约束体几何形状，其中二次型曲线(如周衍柏《理论力学》[1]中钢索类)、曲面(如程守珠《普通物理学》[2])占了主要内容。该类型问题对于拓宽学生视野，练习多种数学工具的使用，加深对牛顿定理求解问题的理解都十分有益。然而目前的情形是：几乎所有的例题、习题都对其中的摩擦力进行了回避——题设中必定出现“‘界面光滑’，‘滑动摩擦因数为零’……云云”。究其原因，是因为考虑摩擦后，由于约束的影响，会使得力学方程变为一组耦合的非线性方程组，而且由几何因素的介入，会使得形态复杂，不易求解，因此对含摩擦的情形避而不谈。然而笔者认为此类做法欠妥，因为“摩擦”作为一种常见力，自中学开始便是学生学习讨论的重点对象之一，对于这样熟悉的领域，相关问题已经成功地解决多次，教学上不应一味回避，否则只会挫伤学生的信心，进而对物理理论产生不信任感，无疑对今后的教学十分不利。本文便就此问题进行展开，抛砖引玉，期望获得同行们更多更好的意见建议。经过分析，笔者认为此类型问题只要考虑好约束体的几何特征，经过一些巧妙变化，是可以将方程做简易的、不脱离学生实际情况的线性化处理的。

1 理论推导

1.1 典型问题

(此处选自周衍柏《理论力学》[1]，为方便计算，参数略有改变)

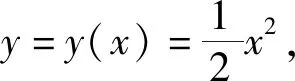
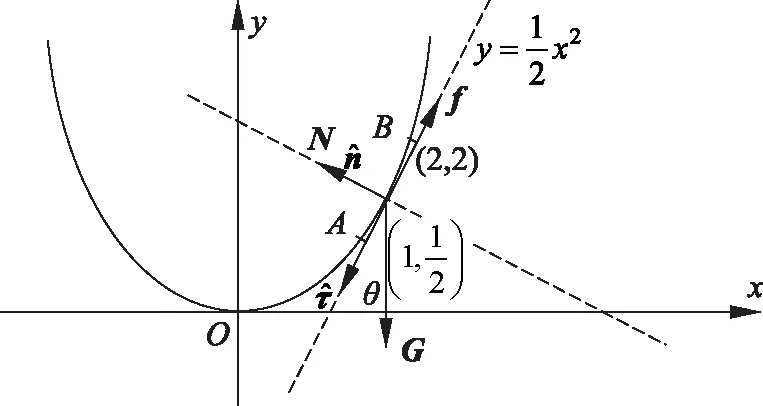
图1 钢索形态示意及小环受力分析图

在钢索上建立自然坐标系，如图1所示，以小环滑动方向为切向(以便在进行速度的投影时确保速率的值恒正)，将动力学方程在自然坐标系中投影为分量形式：

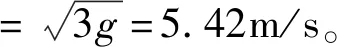
此问题容易求解的原因在于两个方向没有耦合，体现出来的是微分方程性质为线性的，且为可直接变量分离、进行积分的形式。这是目前大学物理教学给予学生的常见习题(及例题)。在此基础上的问题变形基本可分为3大类：(1)钢索开口向下，由顶点开始给予小环一冲击使其获得初始速度，讨论之后的运动情况；(2)转换为半约束的问题，如程守珠《普通物理学》[2]，此类型问题因为是处理一些特殊点，往往最终化为代数方程讨论；(3)更换曲线形态，这种情形除具体处理中考虑一些几何因素之外并无实质的变化。然而一旦去掉“光滑”这一特殊条件之后，情形就变得艰难：

受力分析须考虑摩擦力部分，故牛顿第二定律变为：G+N+f=ma，同样在自然坐标系中进行投影，得：

其中，因为钢索形态描述为连续可导函数，因此与小环接触面视为小平面，故滑动摩擦力沿切线反方向(与速度相反)，同时注意到小环受到滑动摩擦力与钢索给予的正压力满足简单关系：

f=μN

(3)

因此：

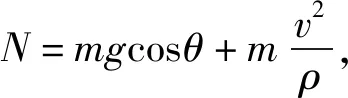
(4)

v2项的引入使得切向方程性质变为非线性，正余弦两个角参量的介入也使得该方程难以直接进行变量分离，同时还得考虑与钢索形态有关的曲率半径项，这都使得直观上要给出该方程解析解似乎是不可能的。经过分析，笔者认为此问题的关键在于解决v2项以及找到对曲率半径的复杂表示进行化简的技巧，而且基于“多数类似题目中的约束体形态都是二次型”这一事实，我们提出沿着不同的路径进行的两种办法：化为可分离变量的形式进行积分求解以及构造成标准一阶线性常系数非齐次微分方程，以通解形式给出结论。

1.2 解法一： 分离变量法

前面提到，因为在大学物理阶段学生遇到的问题中约束体形态较多情形下均为二次型，同时就求解微分方程而言，学生在对数学工具掌握还不够系统熟练的时候，总是期望能以大学物理课本上所演示的办法进行变量分离后再积分。因此，我们首先尝试这一操作办法，将证明当约束体为二次型曲线时，原切向方程可化为以分离变量求解的形式。

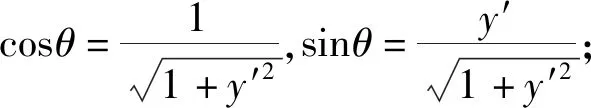
(5)

此处的重要技巧便是对v2项进行变形处理：

(6)

选择vx为新变量，将原方程右侧变形为

(7)

注意其中角参量增向与s增向刚好相反[3](这是由于我们希望保持速率本身恒正所做的切向选择所导致的结果),故：

(8)

代入，得

化简得：

(9)

若y″>0，则：|y″|=y″

移项得：

于是获得可分离变量的形式：

(10)

式(10)化为

(11)

至此，我们证明了当约束体为二次型曲线时，原切向方程可化为以分离变量求解的形式。

积分，得：

(12)

由约束的几何性质，得：

(13)

1.3 解法二： 一阶线性化方程法

当约束体不再是二次型，而是具备更高阶的导数的形态时，由前所述，无法再进行直接的变量分离。但依然不想就此放弃解析法而转向数值计算，因此希望找到具有普适性意义的“线性化办法”。(与法一推导重复部分略)由：

此处关键步骤在于，为线性化方程，需考虑将速率平方作为新变量，而为了达到此目的且同时将复杂的几何参量一并消减，需对右侧部分使用一些形变技巧：

于是，得：

令φ=φ(x)=v2

得φ′+P(x)φ=Q(x)

(16)

其中，

可见我们成功地将原切向方程化为关于φ(x)的一阶线性非齐次微分方程，至此便有了求解此类问题的一般化方法：

首先求解该方程对应的齐次方程φ′+P(x)φ=0，得通解

(17)

再用常数变易法[3]给出特解：

(18)

其中常数C0需由初始条件定出。

2 计算结果

(1) 解法1：以原题为例，根据实验规律，无润滑的钢面摩擦因子在0.1～0.12之间，此处取μ=0.1，与已知条件一并代入计算，得：

(19)

(2) 解法2:

因此

(20)

(3) 对比：

解法一：vA=5.13m/s；解法二：vA=5.15m/s；不带摩擦情形：vA=5.42m/s；可见考虑滑动摩擦后，在题设情形下小环到达A点的速率会略微下降，两种办法解的值差异来源于数值计算与解析计算不同具体过程，尤其在精度的取舍上有所差别。因相对误差小于0.3%，符合物理情景。另外，解法二虽具有普适性，针对具有任意阶导数的约束体均可使用，但在求解过程中遇到的积分形式通常会比较困难。同样针对二次型，解法一可给出解析解，解法二虽给出了解的表达，但积分部分依然需要用到数值计算。

(4) 为更清晰的看到摩擦因数的影响，以及小环在钢索上不同位置的速率情况，以原题为模型作3D图像给予展示(其中摩擦因数取值范围从0～0.25，见图2)。

Plot3D[{9.8*((5/(1+x2))*ⓒ2*μ*(ArcTan[x]-ArcTan[2])-1)*(1+x2)},{x,0,2},{μ,0,0.25},AxesLabel→{"x","μ","v2"}]

图2 v2-x-μ图像

3 分析

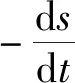
依然可进行变量分离:

这里需特别注意的是，当打开绝对值号后，必须同时考虑路程增量与角参量增量方向变为一致，消去之前方程右侧的负号，才能求解，否则将无法因式分解。

(3) 解法二的核心思想是：将原方程化为一阶线性非齐次常微分方程。主要技巧：(1)考虑变量关系，将关于s(t)的二阶非线性常微分方程组化为关于v(t)的一阶方程；(2)再以速率平方为变量去掉二次项，进一步化简为线性方程；(3)利用轨道的几何特征，找到若干变量之间的约束关系进行化简；(4)利用数学中成熟的处理一阶线性常微分方程的办法——常数变易法进行求解。而这些办法均为学生在高等数学中已经掌握的基本方法，通过这样的计算会极大地增强他们解决问题的信心并从中获得自我肯定。

(4) 从图2可见，当钢索光滑时，小环下滑的速度随高度的下降单调增大，这与机械能守恒定律相符；但考虑摩擦后，由于能量的损耗，导致小环速度的增势不再呈单调性，而是出现拐点，从图2中大致可见：当摩擦因子μ达到0.1时，拐点约出现在x=0.75附近；且随着μ的增大，拐点也向增大的方向变化。整体而言，拐点在3D图像上的分布呈一近直线的形态(曲率较小)。

4 结语

本文针对“大学物理课程中对含钢索类约束的质点动力学问题均未考虑滑动摩擦的影响”这一现状，分析了造成此情况的原因：方程的非线性特征导致求解的困难。对此，本文提出了变量分离及线性化方程两种解决办法，通过论证，表明当约束体为开口向上的二次型曲线时，原切向方程可化为以分离变量求解的形式，而二次型曲线作为常见情形，使得这一处理技巧虽不具备普适性但仍有重要意义；然后针对一般约束体的情形，指明了只要该约束体满足连续可导的数学特征，均可通过变量代换对方程进行简单的线性化，进而导出了一阶线性非齐次常微分方程，并给出解的积分表达式。最后以一典型题目为例，讨论了摩擦力的具体影响。