量纲理论与量纲分析法的教学方案的探讨

魏 环 许贺菊

(华北理工大学理学院，河北 唐山 063210)

量纲分析是物理与工程研究中的一种重要的科学分析方法。科学方法的教育价值主要体现在对学生能力的培养上，所谓“授人以鱼，只供一饭之需，授人以渔，则终身受用无穷”, 就是对科学方法的教育价值的最通俗的表述。学生的学习能力、研究与解决问题的能力乃至创新能力不仅依赖于他们所掌握的知识，更依赖于他们对科学方法的认知程度。

量纲分析法在西方许多大学物理教材中都有较长篇幅的详细介绍[1]，反观我国的基础物理教学，对量纲分析理论的重视程度还远远不够，赵凯华先生在1991年出版的《定性与半定量物理学》一书中就谈到：“在通常的物理教科书中，量纲理论往往只是顺便提及和一带而过。关于量纲的应用，在教学中也只介绍单位的换算、检查公式的对错等少数方面[2]。”时至今日，20多年过去了，赵先生所谈之状况仍未有多少改变。追寻导致“一带而过”这种教学现状的原因，本文认为，主要是在我国的大学和研究生院的课程设置中，很少有院校把量纲分析当作一门课程来开设，那些教授和使用量纲分析法的也仅仅是涉及传热学、力学等极少数专业的教师和学生，因此，许多从事物理教学的教师本身就对量纲分析法及其应用缺乏了解和研究，物理课堂上的量纲问题最终就只能“一带而过”了。

量纲分析理论具有重要的教育教学价值，这是一个能够使学生长期受用的知识和方法，在大学物理课程中不应“一带而过”，而要给予足够的重视，这也是作者撰写此文的初衷。

1 量纲分析法的理论基础

1.1 量纲的意义

每个物理量都有两个基本特征，那就是它的大小和属性，物理学中的单位和量纲就是与此相关的两个概念。其中，物理量的单位是为了度量物理量的大小而人为规定的参考标准[3]，而量纲则是为了表征物理量的基本属性以及辨识物理量的种类而采用的术语。在任何一个单位制中，都会有一组物理量被选作基本量，每个基本量均具有独立的量纲，导出量的量纲由基本量的量纲组成。

1.2 物理量的量纲式[1，4-6]

一个导出量的量纲由单位制中基本量纲幂次的乘积来表示。按照国际标准，一个物理量Q的量纲记为dimQ，其量纲式为：dimQ=AαBβCγ…，其中，A，B，C …表示某个单位制中的基本量纲，α，β，γ…为实数，称为物理量Q的量纲指数。在国际单位制中共有7个基本物理量，对应有7个独立的基本量纲(L、M、T、I、Θ、N、J)。因此，物理量Q的量纲式为

dimQ=LαMβTγIδΘεNξJη

(1)

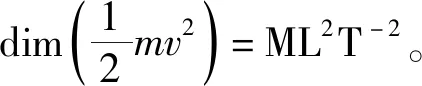
物理量按其属性分为两类：一类是物理量的大小与选用的单位制有关，称之为有量纲量，例如长度、时间、能量、动量；另一类是物理量的大小与所选用的单位制无关，这类物理量的特征是其量纲指数均为零，故称无量纲量，例如，两个同类物理量的比值、角度、指数和对数等超越函数的变量、精细结构常数，等等，均为无量纲量，此类物理量均用纯数来表示。

1.3 量纲和谐原理

量纲的运算服从指数运算法则：两个物理量相乘时其对应的量纲指数相加，相除时其对应的量纲指数相减。比较物理量的大小只有在属性相同(即量纲相同)的物理量之间进行才有意义，同样，只有量纲相同的物理量才能相加、相减或相等。

物理规律必须具有度量单位变换的不变性，因此，一个正确反映客观规律的物理方程，其等号两端必然是量纲一致的，即物理方程式中各代数项的量纲必须相同。这个量纲法则又称“量纲和谐原理”[5,6]。

1.4 量纲分析法

物理规律指的是在某个物理现象或物理过程中，存在于原因与结果之间的必然联系，从量纲的角度看，反映因果规律的物理方程必然服从量纲和谐原理。当选定了某个单位制后，每个物理量也随之有了确定的量纲式，此时，“量纲和谐”作为法则必然对原因与结果的物理量之间的依存关系构成制约，即，量纲和谐原理从量纲的角度已然规定了一个过程中各个物理量之间的内在关联。因此，该原理当然就能够成为分析和判断物理现象中因果关系的重要依据，即：从量纲和谐原理出发能够分析和寻找物理现象中的客观规律，或者依据该原理可以去寻找解决复杂问题的线索。

所谓量纲分析法，就是利用物理量的量纲所提供的信息，根据量纲和谐原理这个法则去确定一个物理过程中各个物理量之间的因果关系并建立数学模型的方法[4-6]。

1.5 两种常用的量纲分析方法

1) 瑞利分析法

瑞利(L.Rayleigh)积极提倡使用量纲分析法，他给出了一种直接利用量纲和谐原理建立量纲等式来确定物理量之间因果关系的分析方法[7]，该方法基本步骤如下：

(1) 对于待求物理量，确定对其构成控制或影响的相关物理量以及所涉及的基本量纲。譬如设p为待求物理量(因变量)，p1，p2，…，pn为影响p的n个物理量(自变量)，用k表示为自变量和因变量中所涉及到的基本量纲的数目。

(2) 建立物理量之间指数乘积形式的因果关系式。即设

(2)

其中，λ是无量纲的未知系数，a1，a2，…，an为待定幂指数。

(3) 依据量纲和谐原理，写出式(2)的量纲等式：

(3)

(4) 根据每个物理量在所选用单位制中应有的量纲式以及量纲等式(3)，列出a1，a2，…，an所满足的方程组。这里以力学问题为例，采用国际单位制则基本量纲的数目k=3，涉及到的基本量纲为L、M、T，因此，可设

代入式(3)，有

可得以a1，a2，…，an为未知量的方程组：

(4)

(5) 解方程组，确定幂指数a1，a2，…，an的取值，获得含有未知系数λ的因果关系式(2)。

λ是需要通过实验或理论分析来求取的，故采用瑞利分析法只能得到定性的因果关系。此外，基本量纲的数目k决定了由量纲恒等式列出的代数方程的个数，当n>k时，将无法唯一确定a1，a2，…，an的取值。因此，瑞利分析法受到物理量个数n的限制，它更适合处理n≤k的问题。

2) Π定理与无量纲化分析法

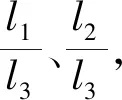
在量纲分析法中，对相似的物理现象的共同特征，也采用一组相似特征数来表征。但是，与对几何相似性的描述不同的是，由于控制或影响一个物理现象的物理量可以有多个，而且属性也不同，因此，这组无量纲的相似特征数通常是由属性不同的物理量组合而成的[4]。

由于过程中相关物理量之间有着确定的因果联系，因此表征该过程的相似特征数之间也必然存在着确定且等价的函数关系。1914年，E. Buckingham从量纲和谐原理出发，推导和证明了“有量纲的物理量之间的因果关系与无量纲的相似特征数之间因果关系的等价性”[8]，该定理表述如下。

如果某个物理问题中涉及n+1个物理量p0，p1，p2，…，pn(其中可以包含物理常数)和k个基本量纲(n+1>k)，则由此可以组成n+1-k个无量纲的量Πi(i=0，1，2，…，n-k)。而在物理量p0，p1，p2，…，pn之间存在的函数关系式

p0=f(p1，p2，…，pn)

(5)

可以等价地表达成相应的无量纲形式

Π0=F(Π1，Π2，…，Πn-k)

(6)

Πi即相似特征数(由于它们都用Π表示，此定理又称Π定理)，式(6)也称相似特征数方程。Π定理表明，任何一个有量纲的物理方程改写为无量纲量组成的方程时，其规律性不变。

相似特征数Πi的构成方法如下：如果问题中共涉及k个基本量纲，则可在n+1个物理量p0，p1，p2，…，pn中选择k个具有独立量纲的物理量作为一组基本量去度量其余的物理量，即可得到n+1-k个无量纲量。比如，取p1，p2，…，pk作为一组基本量，则

其中ai1，ai2，…，aik为一组待定幂指数，可以根据每个物理量的量纲式以及Πi的零指数性质，确定出ai1，ai2，…，aik的取值。结合式(6)、式(8)，有:

(9)

由于相似特征数均独立于单位制，也与实际问题中物体本身的大小和运动规模等具体物理量无关，具有客观性，因此，相似特征数方程反映的是彼此相似的同一类物理现象所遵循的规律。

3) 模型试验与物理相似原理

利用三角形的几何相似性，古埃及人测出了金字塔的高度。同样，对于那些不适于直接针对实物进行实验的复杂的工程技术问题，人们采取了用模型实验来代替对原型(即工程实物)直接进行实验的研究策略。模型实验是指在模拟的环境中，针对经过缩减的实物模型、运用简化及可控制的方法再现和研究实物实际发生的物理现象。由Π定理可知，相似特征数方程代表了同一类物理现象的本质规律，因此，当模型实验和原型实验满足物理相似的条件时，就可以通过模型实验来发现原型的规律。

由式(6)可知，当模型(用下标m表示)与原型(用下标p表示)中同名的相似特征数对应相等时，即

(10)

模型与原型必然遵循相同的规律，故，同名的相似特征数大小相等是两个物理现象相似的充分必要条件。式(10)是模型实验必须遵循的相似原则，也称物理相似原理[2，4，9-10]。

针对飞机模型、高速列车模型所设计的风洞实验，针对水坝模型、桥梁模型所设计的水流实验等等皆属模型实验。利用模型实验，人们一方面可以再现原型实际会发生的物理现象，另一方面，人们还可以通过对模型的改动来达到对设计系统的原始设计要求。在实践中，相似特征数可以通过量纲分析获得，其具体数值则由模型实验来确定，这些数值可以直接应用于原型以及其他相似的物理现象中。可见，Π定理与物理相似原理是模型实验的理论依据。

4) 对两种量纲分析法的评析

第一，无论是瑞利分析法还是无量纲化分析法，都是将量纲和谐原理作为探寻事物间因果规律的根本原则。这种观察和分析问题的视角、原则与逻辑，不需要已知具体的物理定律和机理，甚至并不要求研究者具备足够的专业知识，因此，当人们面对那些物理机理尚不清楚、亦无现成数学模型可用的复杂现象时，量纲分析将能提供行之有效的建模途径。

第二，在上述两种分析法中，式(2)中的系数λ及式(6)中函数F的具体形式均不能依靠量纲分析法来确定，而是需要通过具体实验或理论分析才能获得。因此，量纲分析法仅限于对物理问题进行定性的分析。

第三，在瑞利法中只需要通过实验确定一个系数λ即可，而Π定理提供的无量纲化分析法可以使自变量的个数由n个减少为n-k个，二者均能够大幅减少实验环节的工作量。

2 量纲分析理论的三层次教学方案

2.1 确立“完整且有深度”的教学目标

从教学的角度看，量纲分析理论的特点之一可以用“基本”二字概括：首先是概念基本，量纲是对一个物理量属性的描述，而属性是每个物理量的基本特征之一；其次是原理基本，量纲和谐原理是任何一个正确反映客观规律的物理方程都要遵从的基本法则；第三是应用基本，利用量纲概念可以在同一单位制中进行单位换算，利用量纲和谐原理可以检验方程中各个物理量之间的关系是否正确。量纲概念及其基本法则是每个物理学习者登堂入室所必须掌握的基础知识。

特点之二，作为一种研究方法，量纲分析法有着独特的视角和非常规的思维方式：它既不依赖已知的物理定律，也不采用从已知物理定律出发进行逻辑分析最后得出结论的常规思维方式，而是选择量纲作为考察与分析问题的视角、将“量纲和谐”这一基本法则作为在探寻客观规律时进行逻辑分析与判断的基本依据。正是这种独特的视角和非常规的思维方式，使之成为人们在处理机理尚不清楚且无现成数学模型可用的复杂的物理和工程问题时首选的研究方法[4，11-15]，事实表明，这种方法往往能够发挥非常重要而有效的作用。

此外，量纲分析不受具体专业的限制，是具有普适性的方法，这是其特点之三。

对于量纲分析这个基本且重要的科学方法，大学物理课程理应对其作出完整且有深度的介绍。在此，“完整”是指对量纲不能只介绍它的基本功能，还要介绍量纲分析法的核心理论——Π定理；而 “深度”是强调，在教学环节中不仅要有通透的理论分析以揭示方法的内涵，还要有恰当的示例以展现其应用的价值。只有这样才可能让学生对这种方法形成良好的认知。深度与完整是相互关联的，不完整则无法有深度。

2.2 关于“三层次教学设计方案”

基于上述目标，并且依照量纲分析理论的内在逻辑，设计如下3个教学层次：

第一个层次，介绍量纲的基本概念、原理和最基础的应用功能，使学生建立起量纲的概念，接受量纲和谐的思想和量纲分析的基本法则；

第二个层次，介绍瑞利分析法。基于Π定理的无量纲化的分析方法虽然更为基本，但它同时也很抽象，而瑞利分析法逻辑简洁明了，是对量纲和谐原理的直接运用，把对它的讨论作为第二个教学层次，会让学生在逻辑思维的衔接上感觉连贯和顺畅，既有利于学生的理解，也有助于巩固和强化学生对量纲法则的认知。

第三个层次，介绍Π定理及物理相似原理。由Π定理提供的无量纲化的分析方法更加普适，特别是它与相似原理的联合运用，不仅成为模型实验的理论依据，也成为了目前广泛应用的数值模拟方法的理论基础。因此，介绍Π定理与相似原理是量纲分析理论在当今的大学物理课程中应该达到的教学深度。

上述3个教学层次是按照量纲分析法的内在逻辑组织构建的，因此，知识脉络清晰分明。此外，尽管量纲分析法需要学习者具备一些基本的物理常识，但是方法本身并不需要依赖具体的物理规律，所以，完全可以在大学物理课程之初的力学部分中，将这3个教学层次集中作为一个独立授课单元去讲授。因为，对于有着高中物理基础的大学生而言，介绍量纲分析法无需更多知识来铺垫。

物理学是具有方法论性质的基础学科，科学知识与科学方法应该是大学物理课程中两个平行的主体内容。科学方法涉及的是人们认识世界的思维方式与行为方式，承载着与知识不同的教育内涵与教育价值[16]。教育的一个重要特点就是有意识、有目的的影响人。拿出一定的学时明确完整地教授一种科学研究方法，这种具有明确目的的教学设计可以促使学生有意识地接受科学方法的训练，也有助于学生对科学方法形成全面和系统的认知[17]。

3 3个量纲分析示例的教学赏析

例题分析的作用重在点化学生，教师通过对精心挑选的示例展开分析讨论，以期达到启迪学生心智、深化其认知和拓展其思维的教学目的。

示例1：用量纲分析法证明勾股定理[2，11]。

证明：面积S的量纲为dimS=L2，由图1可知，当直角三角形的斜边长度一定时，其面积还取决于锐角θ的函数f(θ)。由于角度θ及其函数f(θ)均无量纲，根据量纲和谐原理，斜边长为c的直角三角形的面积可表示为S=c2f(θ)。

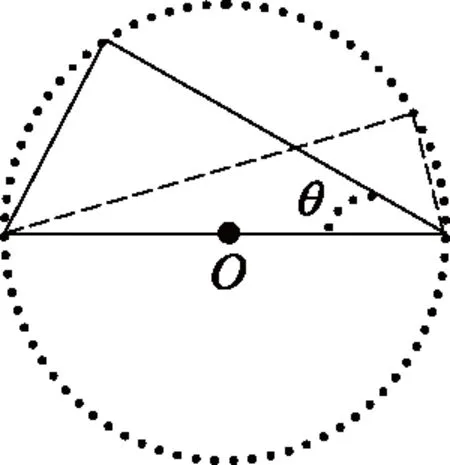
图1 直角三角形的面积

图2 证明勾股弦a、b、c的关系

如图2所示，对直角三角形的斜边做垂线，可将该三角形分成左右两个与之相似的直角三角形，这两个小的直角三角形的面积亦可以表示为

S左=a2f(θ)，S右=b2f(θ)

由于S=S左+S右，得到：c2f(θ)=a2f(θ)+b2f(θ)，消去f(θ)，即有c2=a2+b2成立。

教学赏析：

示例1运用量纲分析的思想、以简洁明快的物理方法对学习者早已熟悉的数学定理给出了精彩的证明，这让初学者在对量纲分析法的功能感觉奇妙和兴奋的同时，也大大激发了他们进一步了解和学习这种方法的兴趣，这样的教学效果在作者多年的教学实践中屡试不爽，将此示例作为激发学生兴趣的首例当是绝佳选择。

此示例依据量纲和谐原理以及面积和角度这两个物理量的量纲完成了对直角三角形面积的数学表达，这是整个逻辑推理过程的第一步也是最为关键的一步，它对学生学习从量纲的视角观察和分析问题具有引导和示范的作用。另外，逻辑分析的线索是量纲，论证过程也与单位无关，表明量纲的“功能”是无法由单位取代的，在此可引导学生体会量纲的意义、厘清量纲与单位在功能上的分别。

示例2：利用瑞利分析法研究物体做自由落体运动的时间。

解：由于地球引力导致了物体下落，故根据经验推测，物体自由下落的时间t应该与物体的下落高度h、物体的质量m以及当地的重力加速度g有关，可设：t=λhαmβgγ，采用国际单位制，有量纲等式

T=LαMβ(LT-2)γ=Lα+γMβT-2γ

结论：第一，自由落体运动的时间与下落物体的质量无关；第二，如果在考虑地球引力作用对时间的影响时，选择的是地球质量 而非重力加速度，则此方法无解，这是量纲分析法本身的局限性，准确找出影响和控制物理过程或现象的因素是有效运用量纲分析法的前提和关键。

教学赏析：

示例2不仅展现了量纲分析法本身的逻辑顺序，同时也将它的许多特性展现给了学生：(1)定性分析的特征；(2)不依赖已知的物理规律；(3)方法本身的局限性。

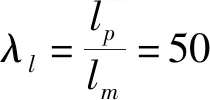
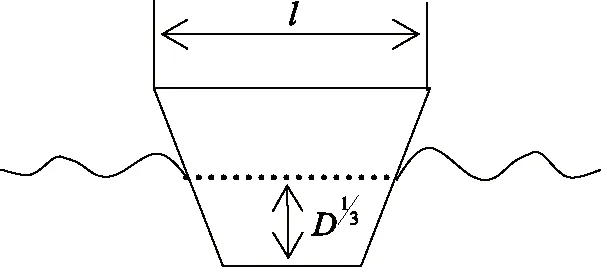
图3 船舶的阻力

解：在水面行进的船舶所受到的阻力F由两部分组成，一是由水施加的黏滞阻力，二是行进中的船舶造成水面波浪因消耗能量而形成的波浪阻力，为重力效应。因此，与阻力F有关的是表征船舶外形的特征长度l、与载重量有关的排水体积D、船舶行进速度v、水的密度ρ、水的黏性系数μ及重力加速度g。故，

F=f(l,D,v,ρ,μ,g)

本例只涉及力学的3个基本量纲，根据Π定理，在影响阻力F的6个变量中选取l、v、ρ这 3个具有独立量纲的量为基本量，则阻力F的无量纲表示式为

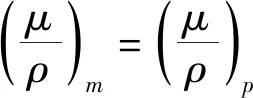
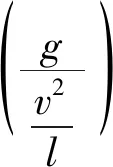
必须要求：

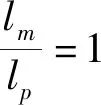
(1)Fp=503×0.02=2500(N)

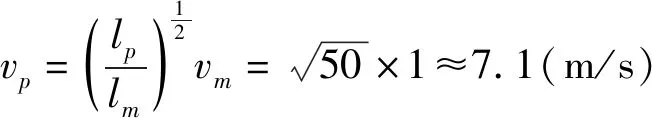
教学赏析：

示例3是流体力学中的一个典型模型实验问题，对它的分析与推理，既涉及了对Π定理和物理相似原理的具体运用，也涉及了在解决实际问题时对物理学的近似原则与方法的运用，因此，这是一个能够较为全面地展示如何运用量纲分析法解决复杂的物理与工程问题的理想的教学示例。

本示例不是一个纯粹的物理学基础理论问题，而是一个与模型实验相关的具体工程案例。这样设计的宗旨如下：第一，展示运用量纲分析法解决工程技术问题的逻辑和步骤。量纲分析理论在基础物理学中有着许多重要的应用，但是此方法在研究物理现象中的未知规律时具有独特的作用，为非物理专业的理工科学生提供用量纲分析法解决工程问题的案例，对他们的吸引力以及思维方式的影响会更大。第二，通过对实例的感受，化解理论的抽象。由于以Π定理为代表的无量纲化分析法较为抽象，因此，选择此示例的目的，是希望通过对这个具体案例的教学分析，能够起到化解理论的抽象性、降低学生认知难度的作用。

本示例主要不是为了让学生学习流体力学的相关理论而是展示无量纲化的分析方法，尽管学生对于描述流体黏性的物理量比较陌生，但是不会因此增加他们对方法本身在应用方面的理解难度。可以将其放在大学物理的力学部分，完成对量纲分析法的第3个教学层次的教学目标。

本文为三层次教学方案推荐了3个示例，一层一例，由浅入深，由简到繁，能够基本实现完整且有深度的介绍量纲分析法的教学宗旨。

4 结语

对理工科学生而言，是否具备了运用科学知识、科学的思维方式和行为方式分析和解决实际问题的能力，是评判其科学素质优劣的一个重要尺度。本文以加强科学方法教育、培养学生创新能力为目的，针对目前在物理教学中仍被忽视的量纲分析法，阐述了量纲分析法的核心教学内容与教育教学价值，同时，结合作者多年教学实践经验以及相关研究成果[15]，对完整而有深度的讲授量纲分析法提出了教学建议，希望本文能够对推动量纲分析法的物理教学研究发挥一定的作用。