牛顿环实验的数据处理改进及图像分析

朱晓梅 向伟铭 姜向东

(西南交通大学物理科学与技术学院，四川 成都 611756)

牛顿环是光的一种薄膜干涉图样，最早是由牛顿于1675年首先观察得到的，当用单色光照射牛顿环装置时，在视觉上为一系列明暗相间的同心圆环。这些圆圈的距离不同，随着到中心点的距离增加而逐渐变窄，它们是由球面上与平面上反射的光线相互干涉而形成的干涉条纹。以往实验室通常使用的逐差法处理实验数据，过程较为繁杂，其计算结果也不够准确。在牛顿环实验中获得的某组数据通过逐差法计算牛顿环透镜曲率，其相对扩展不确定度为0.82%，由于“逐差”先两两相减使得自由度减半，即重复测量或组合测量时计算实验标准偏差所用的独立残差个数减半，未能充分利用测得的有效数据信息，这不符合实验设计随机化原则的思路。本文通过线性拟合法处理实验数据，并利用GUI建立一个可进行数值分析以及图像动态分析的交互式界面，不仅可以得到更精确的实验结果，其相对扩展不确定度为0.65%，还能结合实际选择牛顿环实验参量以观察到不同的实验现象，简便易行，应用范围广。

1 牛顿环实验理论

牛顿环装置如图1所示，牛顿环干涉的明暗条纹条件满足：

得到牛顿环暗纹公式[1]

由于单色光的波长λ已知，测量得到第k级的暗环半径，可以计算得到牛顿环凸透镜的曲率半径。由于中心切点处的压力形变或残留粉尘作用，实际方程式由上式修正为

(1)

图1 牛顿环装置示意图e指的是牛顿环装置中的凸透镜和底面平板之间的厚度距离

2 传统实验数据处理方法——逐差法

考虑到凸透镜和平面镜表面的尘埃和凹陷，以及波长误差、平晶不平度、部分余弦(投影)误差、被测面偏离理想球面等误差使得显微镜观察下的牛顿环中心将会是一个圆斑。于是改为测量牛顿环的各暗环直径即可避免这种误差。若求得了第m级及第n级的暗环直径Dm,Dn，记m-n=25即可得到计算公式：

(2)

此时已知单色光源为钠光灯，其波长λ=589.3nm，通过逐差法即可计算得到曲率半径R。具体的逐差法计算结果见表2所示。(其中XL,XR分别表示某暗环中心在牛顿环左侧和右侧的位置)

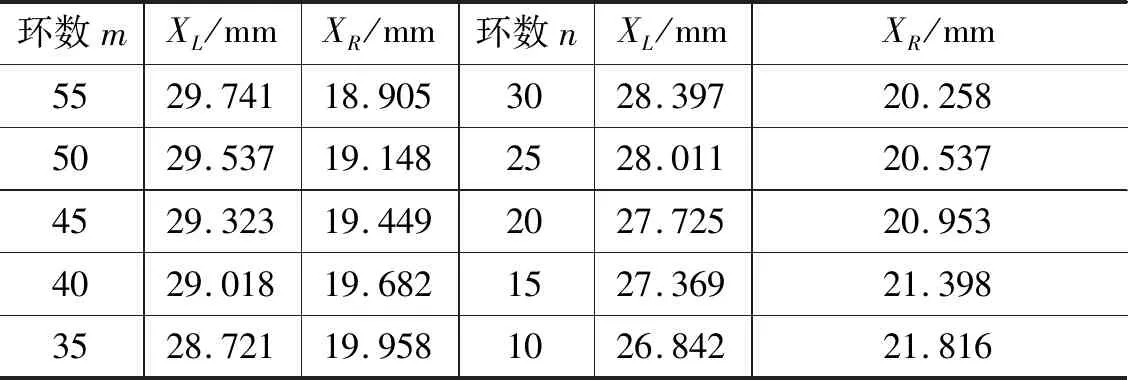
表1 牛顿环各级暗环半径位置记录表

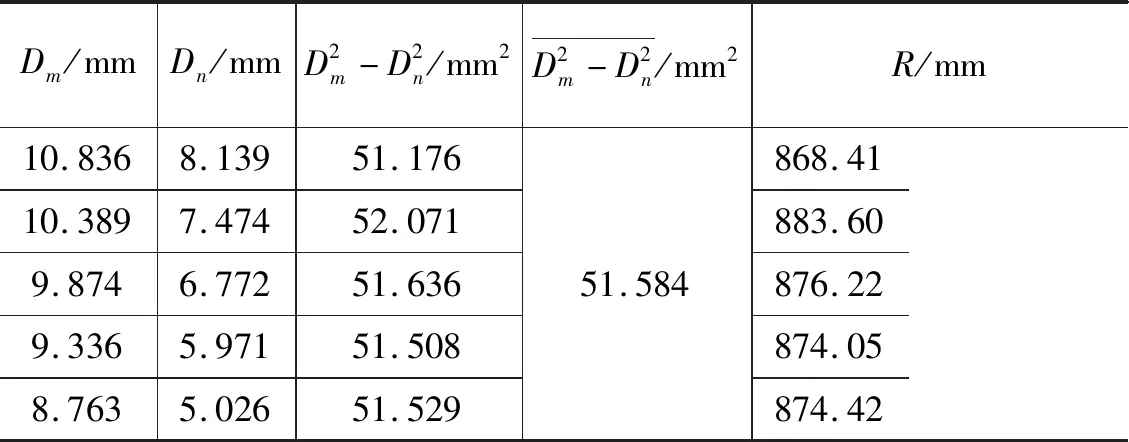
表2 逐差法处理数据结果

(3)

其中UDka即瞄准误差限，通常是直径测量不确定度的主要因素之一[3]。

先考虑到仪器误差限带来的B类不确定度分量，实验使用的是含有滚珠丝杆和1级螺纹副的测量显微镜，其误差限ΔINS≈0.05,由B类仪器误差限分量的相对不确定度公式得到B类相对不确定度第一项分量：

再考虑到瞄准误差限带来的B类不确定度分量，由B类瞄准误差限分量的相对不确定度公式得到B类相对不确定度第二项分量：

下面计算逐差法的B类方和根，使用扩展不确定度的计算公式[2]：

其中t为自由度ν=n-1=4，在置信水平0.95时的学生氏t分布的值，满足下列公式

(4)

B类相对不确定度合成为

此外，符合1-α=0.95的A类相对扩展不确定度为tsb1/b1=0.8%

3 实验数据处理的改进技术和方法

考虑到“逐差”先两两相减使得自由度减半，因而未能充分利用测得的有效数据信息。并且其操作计算步骤不具有简便性。由式(1)知：

将离散的牛顿环曲率半径平方值与暗环级数画在一个坐标图中，如图2所示。

图2 牛顿环暗环半径平方与暗环级数散点图

由图2知二者近似地成一次关系。对这些离散的点进行线性拟合所得曲线的斜率代表凸透镜曲率半径R和单色入射光的波长λ之乘积。因此牛顿环凸透镜曲率半径R亦可通过线性拟合法计算得出。

4 线性拟合处理实验数据

根据上述计算原理计算得到最后的拟合结果，通过自制的GUI界面直观方便地呈现，如图3所示。

图3 牛顿环曲率半径计算GUI界面

计算透镜曲率半径值为：R=873.15mm。

针对瞄准误差限带来的B类不确定度分量，由线性拟合斜率扩展不确定度的计算公式[2]：

sb1为拟合直线斜率b1的标准差。满足下式：

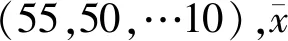
5 实验结果分析对比

对两种处理得到结果的相对不确定度进行分析比较，由相对不确定度的计算公式：

(5)

表3 逐差法和线性拟合处理数据相对扩展不确定度的对比表

6 牛顿环图像动态分析模拟

除了上述数值分析的模拟之外，对牛顿环图像的分析也可通过该GUI界面进行模拟。利用计算机进行牛顿环图像的仿真处理[4]， 仅考虑通过对干涉光强的模拟而绘制图像，并未结合实际情况中入射单色光波长与凸透镜曲率半径的取值，造成图像分析较为片面。考虑到实际选取的入射光波长有一定的取值范围，该界面提供两种波长的选取方式。可以模拟实验室进行牛顿环实验的常用单色光，如钠灯、汞灯，通过弹出式菜单即可选取；亦可通过滑动条任意选取位于可见光范围内的波长。移动各滑动条就可以改变凸透镜的曲率半径取值。

牛顿环图像的模拟选取波长为420nm的单色光照射，凸透镜的曲率半径为520mm，得到牛顿环图像如图4所示。实测暗环第5环、第15环、第25环的直径依次是：2.087mm、3.621mm、4.669mm。

图4 初始牛顿环图像

图5 改变曲率半径参量后的牛顿环图像

控制波长不变，增大凸透镜的曲率半径至1325.5mm，得到牛顿环图像如图5所示。实测暗环第5环、第15环、第25环的直径依次是：3.335mm、5.778mm、7.457mm。

控制曲率半径不变，增加单色光的波长至739.6nm，得到的牛顿环图像如图6所示。实测暗环第5环、第15环、第25环的直径依次是：2.772mm、4.804mm、6.196mm。

图6 改变单色光波长参量后的牛顿环图像

可见由GUI界面所呈现的牛顿环图像得到得以下结论均与实验结果相符：

(1) 若控制单色光波长参量不变，牛顿环各环半径将随着凸透镜曲率半径的增大而增大。

(2) 若控制凸透镜曲率半径参量不变，牛顿环各环半径将随着单色光波长的增大而增大。

7 结语

采用线性拟合法从相对不确定度的相关理论处理牛顿环的实验数据，得到结果的相对扩展不确定度为0.65%，更精确且符合实验设计随机化原则的思路。并且采用计算机程序进行实验的数值与图像模拟，将实验室中繁杂的测量、计算、数据处理过程通过简单的GUI界面表示，排除实验过程中遇到的包括透镜与平面镜之间的压力形变以及调整实验参量进行动态分析较困难的问题。通过计算机模拟与GUI界面的结合，提高实验的准确程度，便于总结牛顿环的实验规律，可以得到更广泛的应用。

致谢: 本文在实验数据的不确定度分析方面得到了清华大学物理实验中心朱鹤年教授的悉心指导，在此表示对朱教授的真诚感谢。

本文在选题、研究和修改过程中得到了西南交通大学物理实验中心姜向东教授的支持和帮助，在此表示对姜老师的真诚感谢。