凸显联系沟通构建数学模型

徐彬

【摘   要】小学数学“解决问题”教学中，“回顾”即再现研究历程，关注思路与结果的合理;“反思”即思考研究过程中的问题和策略，积累活动经验，形成良好的认知结构。“回顾与反思”板块的教学视角，分别是检验解决问题的结果、审视解决问题的思考过程、沟通方法之间的联系、构建不同问题的数学模型。

【关键词】解决问题;回顾与反思;联系沟通;构建模型

一、背景陈述

人教版小学数学教材将“解决问题”分为三个教学板块，即“阅读与理解”“分析与解答”和“回顾与反思”。在日常教学中，教師往往重视阅读与理解、分析与解答，而对于“回顾与反思”板块，教学过程中则是简略带过，似乎可有可无。百度百科中，对于回顾、反思的解释是：回顾指回想过去，思考过去发生的事件;反思指思考过去的事情，从中总结经验教训。而在小学数学“解决问题”教学中，“回顾”可以理解为再现研究历程，关注思路与结果的合理;“反思”即进一步思考研究中的问题和策略，积累活动经验，以形成良好的认知结构。

笔者曾执教《用方程解决问题》（人教版五年级上册第五单元《简易方程》P79例5）一课，特别关注“回顾与反思”板块的设计与实施。为更好地了解学生的基础，笔者对杭州市江干区220名五年级学生进行检测（已学习过《用方程解决问题》一课）。

（一）检测内容和目的

测试内容：甲地到乙地相距3000米，小王和小明两人相向而行，小明每分钟走80米，小王每分钟走120米，问两人几分钟后相遇？（请你把完整的解决过程表示出来）

测试目的：换一种问题情境，要求学生表示出用方程解决问题的完整过程，主要考查学生如何思考，能否解决问题。

（二）检测数据和典型错误

（三）检测分析

关于“回顾与反思”的情况，分析可知：（1）学生缺乏检验的意识，题目明确要求表示完整解决问题的过程，仅有36.8%的学生进行了检验。（2）学生缺乏检验的方法，典型错误3000÷120+3000÷80，一个人行走都只需要25分钟或37.5分钟，两人相向而行怎么会需要更多的时间，求出的答案明显不合理。（3）情境改变后，部分学生没有形成解决这类问题的模型，采用画图分析和检验的学生更是寥寥无几。

基于上述分析思考，笔者在省、市、区教研员的指导下，重点对《用方程解决问题》“回顾与反思”环节展开教学研究，几易其稿后，最终在研讨活动中呈现了一个比较好的课堂结构，广受好评。

二、实践探究与反思

（一）检验解决问题的结果

在教材编写上，对于解决问题检验的习惯培养是非常重视的，从低段开始，一年级上册P46，就第一次呈现了“图里有什么，怎么解答，解答正确吗”。因此，在教学中，要有意识地培养学生检验的习惯，以提升学生解决问题的能力。常见的检验方法有3种：（1）估算，看看解决的结果是否合乎情理;（2）代入，把结果当成已知条件，检验结果是否与已知条件相符;（3）另解，用另一种方法解决问题，检验答案是否一致。

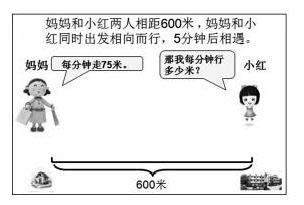
出示题目：“妈妈和小红两人相距600米，妈妈和小红同时出发相向而行，5分钟后相遇。妈妈每分钟行75米，问小红每分钟行多少米？”学生在用多种方法解决问题后，教师这样引导。

师：用方程解决问题，我们怎样可以保证求得的结果一定是正确的？

生：检验。

师：是的，检验是必不可少的。怎么检验？

生：把45代入原方程进行检验。

生：这样能保证这个方程的解正确，但不能保证问题解决是否正确。

生：把问题当成条件代入原来的题目中来算一算。

生：把小红每分钟行45米这个问题当成条件，求两人相距多少米。

师：那就请你们自己动手来检验一下。

生：75×5+45×5=600（米），和原来条件两人相距600米相一致。

生：（75+45）×5=600（米），和原来条件两人相距600米相一致，前面解决问题的结果是正确的。

（二）审视解决问题的思考过程

张丹教授在《“问题解决”目标的内涵及实现》一文中提到，学生在问题解决中的失败常常不是由于他们缺乏数学知识，而是由于他们不能有效地应用所学知识。好的问题解决者常常监控并调整他们解决问题的过程。

在“回顾与反思”环节，就要引导学生不断去回顾解决问题的步骤和解决问题的策略。当然，这时候的回顾主体要明确，不是教师来回顾梳理，而应该是学生在经历解决问题的基础上通过反思，进一步明晰思考程序。

如在例题教学后，教师通过2个问题的驱动，引导学生回顾用方程解决问题的整个过程和加深对解决问题策略的感知，见以下教学片段。

师：同学们很厉害，用两种不同的方法解决了这个问题。我们来回顾一下，刚才是怎样用方程解决问题的？

生：用方程解决问题，首先要找到等量关系—根据等量关系，设未知数列方程—解答并检验。

师：那有什么好办法可以帮助我们找到等量关系呢？

学生通过回顾线段图和等量关系的联系，感受通过画线段图可以清楚地分析数量之间的相等关系，初步形成“画图分析—找等量关系—列方程”的一般过程，进一步深化画图解决问题的策略。

（三）沟通方法之间的联系

众所周知，用方程解决问题的关键是正确理解题意，快速有效地找到等量关系，然后根据等量关系列出方程。在平时教学中，学生常常对复杂的题目无从下手，因为他们不会主动去写出等量关系，对于等量关系的重要性感受不够。本课巧用“回顾与反思”环节，让学生把结果当成条件代入原题进行编题检验，形成多个问题。通过变式编题讨论，既进行了基本练习巩固，更让学生通过每个问题2种方法的比较和4个问题方法之间的沟通，感受到用方程解决问题的等量关系的一致性。

1.变式改编

师：前面检验中，同学们把小红的速度每分钟45米当成已知条件，可以算出总路程，你觉得还能解决什么问题？

学生编出：“妈妈和小红相距600米，妈妈和小红同时出发相向而行，5分钟后相遇，小红每分钟行45米，问妈妈每分钟行多少米？”

“妈妈和小红相距600米，妈妈和小红同时出发相向而行，妈妈每分钟行75米，小红每分钟行45米，问几分钟后相遇？”

2.尝试解决，基本巩固

学生解决问题后，全班交流，通过列方程得出妈妈的速度是75米/分钟，相遇的时间是5分钟，和原来的条件是一样的，也可以检验出我们前面解决问题的结果是正确的。

3.观察比较，感受等量关系的重要性

师：我们刚才解决的这些不同的问题，有什么是相同的？

学生讨论交流后，进一步理解每个问题的2种方法，明确各自的数量关系。还发现，同一情境下的4个问题，它们的基本等量关系是相同的，都是利用“妈妈的路程+小红的路程=总路程”或“速度和×相遇时间=总路程”。一个等量关系可以解决这么多问题，让学会体会到用方程解决问题的优越性。

（四）回顾与反思，构建不同问题的数学模型

周玉仁教授指出，小学生在解决问题的过程中，实际上完成了认识上的两个转化。第一个转化指从纷乱的实际问题中，收集、观察、比较、筛选有用的信息，抽象成数学问题。第二个转化是根据已抽象出来的数学问题，分析其中的数量关系，探究解决问题的方法并求解，进而在实践中检验，必要时还能反思自己解决问题的全过程。

在教学中，教师往往会重视第二个转化，忽略第一个转化，也就是我们所呈现的问题已经从实际问题中抽象出来，没有无效信息和多余信息，指向性明确。而以上两者转化的能力在解决问题中是相辅相成、缺一不可的。本课在新课和练习环节中，创设了5个不同的生活情境，以期让学生能在用方程解决问题中，尝试进行这两个转化。并且让学生在解决散步问题、挖隧道问题、购物问题、面积问题后（问题见下图），与前面的行程问题进行回顾沟通。

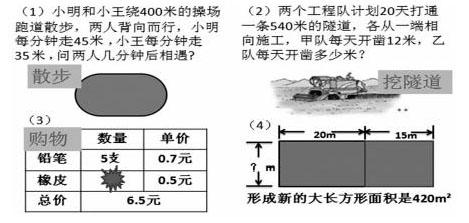
师：这些问题好像都不一样，有没有相同的地方？

生：用方程解决问题的步骤和方法是一样的。

生：这几个问题所列的等量关系都差不多。

師：既然说这5个问题都是相同的，那你能不能用一个含有字母的式子来表示我们今天学的所有的方程？

生：ax+bc=d。

即使购物问题中铅笔和橡皮的数量不同，学生也能感受到这一系列问题内在的等量关系是一致的，都可以用一个含有字母的式子来表示。这能帮助学生找到这些题目之间的内在联系，让学生初步体会两积之和逆解问题的基本模型，建立起解决这一类问题的数学模型。

总而言之，“回顾与反思”的意识和水平，在学生解决问题能力的培养上起着很大的作用，“回顾与反思”其实就是对于学生“元认知”的培养，教师要在解决问题教学中引导学生从不同的角度进行“回顾与反思”，从而提升解决问题的能力。

参考文献：

[1]陈美洁.浅谈小学数学解决问题中的回顾与反思[J].新课程（上），2018（5）.

[2]朱向明.在回顾与反思中提升数学思维——苏教版教材“回顾与反思”的内容编排与教学建议[J].小学数学教育，2015（Z4）.

[3]张丹.“问题解决”目标的内涵及实现[J].江苏教育，2014（11）.

[4]周玉仁.从“应用题”到“解决问题”[J].小学数学教师，2010（7-8）.

（浙江省杭州市东城第二实验学校   310020）