抛物线高考考点扫描

廖庆伟

抛物线是高中数学中的重要内容，也是高考考查的重点，主要考查定义、标准方程、几何性质等基础知识，考查基本技能与基本方法的运用。

一、知识扫描

平面内与一个定点F和一条直线l（l不过F）的距离相等的点的集合叫作抛物线。这个定点F叫作抛物线的焦点，这条定直线l叫作抛物线的准线。其数学表达式为|MF|=d（其中d为点M到准线的距离）。

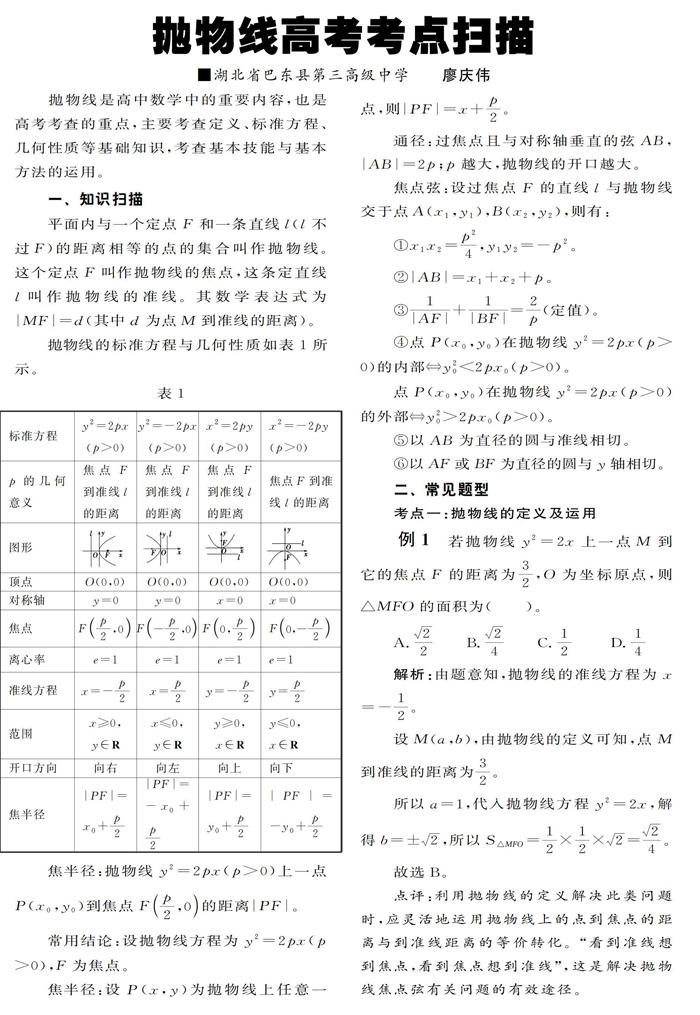
抛物线的标准方程与几何性质如表1所示。

焦半径：抛物线y2=2px（p>0）上一点P（x0，y0）到焦点F（上，0）的距离|PF|。

常用结论：设抛物线方程为y2=2px（p>0），F为焦点。

焦半径：设P（x，y）为抛物线上任意一点，则|PF|=x+-p

通径：过焦点且与对称轴垂直的弦AB，|AB|=2p：p越大，抛物线的开口越大。

焦点弦：设过焦点F的直线l与抛物线交于点A（x1，y1），B（x2，y2），则有：

⑤以AB为直径的圆与准线相切。

⑥以AF或BF为直径的圆与y轴相切。

二、常见题型

考点一：抛物线的定义及运用

例1?若抛物线y2=2x上一点M到它的焦点F的距离为3/2，0为坐标原点，则△MFO的面积为（）。

A.√2/2

B.√2/4

C.1/2

D.1/4

解析：由题意知，抛物线的准线方程为x2。

设M（a，b），由抛物线的定义可知，点M到准线的距离为3/2

所以a=1，代入抛物线方程y2=2x，解得b=±√2，所以S△MPO=1/2X1/2X√2=√2/4。

故选B。

点评：利用抛物线的定义解决此类问题时，应灵活地运用抛物线上的点到焦点的距离与到准线距离的等价转化。“看到准线想到焦点，看到焦点想到准线”，这是解决抛物线焦点弦有关问题的有效途径。

考点二：抛物线的标准方程

例2?如图1，抛物线的顶点在坐标原点，焦点为F，过抛物线上一点A（3，y）作准线l的垂线，垂足为B，若△ABF为等边三角形，则抛物线的标准方程是（）。

A.y2=1/2x

B.y2=x

C.y2=2x

D.y2=4x

解析：设抛物线方程为y2=2px（p>0），则F（ （p/2 ，0 ），B（-p/2，0）。

将A（3，y）代入抛物线方程得y2=6p，y=√6p。

由于△ABF为等边三角形，故kAF=√3，即 √6p-0 /3-p/2=√3 ，解得p=2。

所以抛物线的标准方程是y2=4x，故选D。

点评：求抛物线方程主要有两种方法。

①定义法：根据条件确定动点满足的几何特征，从而确定p的值，得到抛物线的标准方程。

②待定系数法：根据条件设出标准方程，再确定参数p的值，这里要注意抛物线标准方程有四种形式。从简单化角度出发，焦点在x轴的，设为y2=ax（a≠0），焦点在y轴的，设为x2=by（b≠0）

考点三：抛物线的几何性质

例3?如图2，设抛物线y2=4x的焦点为F，不经过焦点的直线上有三个不同的点A，B，C，其中点A，B在抛物线上，点C在y轴上，则S△BCF/S△ACF=（）。

A.|BF|-1/|AF|-1

B.|BF|2-1/|AF|2-1

C.|BF|+1/|AF|+1

D.|BF|2+1/|AF|2+1

解析：如图3所示，抛物线的准线DE的方程为x=-1。

過A作AE⊥DE于E，交y轴于N;过B作BD⊥DE于D，交y轴于M。

由抛物线的定义知|BF|=|BD|，|AF|=|AE|。

所以|BM|=|BD|-1=|BF|-1，|AN|=|AE|-1=|AF|-1。

所以S△BCF/S△ACF=| BC|/|AC |=xB/xA= |BF|-1/|AF|-1故选A。

点评：本题需结合平面几何中同高的三角形面积比等于底边比，抛物线上的点到准线的距离等于其到焦点的距离求解，在平面几何背景下考查圆锥曲线的标准方程及其性质，是高考中小题的热点。

考点四：拋物线中的最值

例4 ?抛物线y2=2px（p>0）的焦点为F，已知点A，B为抛物线上的两个动点，且满足∠AFB=120°。过弦AB的中点M作抛物线准线的垂线MN，垂足为N，则 | MN|/|AB |的最大值为（ ）。

A.√3/3

B.1

C.2√3/3

D.2

解析：设|AF| = =a ，| BF | =b。

由余弦定理得|AB|2=a2+b2-2ab·cos120° = a2 +b2+ab= （a+b）2-ab≥（a+b）2- （ a +b/2）2=/43 （a+b）2。

因为a+b= |AF|+ | BF| =2 |MN| ，所以|AB|2≥3/4|2MN|2，所以 |MN|/|AB|≤ √3/3。故其最大值为 √3 /3，应选A。

点评：解决圆锥曲线中的最值问题一般有两种方法：一是几何意义，特别是用圆锥曲线的定义和平面几何的有关结论来解决，非常巧妙：二是将圆锥曲线中最值问题转化为函数问题，然后根据函数的特征选用参数法、配方法、判别式法、三角函数有界法、函数单调法以及均值不等式法求解。本题是利用抛物线性质及余弦定理、基本不等式等知识求最值的。注意由于抛物线上的点到焦点的距离与到准线的距离相等，所以抛物线的顶点到焦点的距离最小。考点五：拋物线中的定值问题