杯状电极下大电流故障燃弧仿真分析

吴展鸿，周铭标2，陈学军

(1.莆田学院 机电工程学院，福建 莆田 351100；2.国网三明供电公司，福建 三明 365000)

电弧是绝缘体被电压击穿后，由不导电变成导电并发光发热的自然现象。故障电弧是一团高温高压的等离子体，核心温度达到1×104K以上。现阶段大部分绝缘材料都难以承受电弧的核心温度，即使金属材料也难以承受如此高温[1-2]。故障电弧是电气线路中常见的安全隐患，经常发生在线路绝缘不良或接触不良处，也可能发生在松动的电线连接处，以及老化或破损的线路中和电器线路的连接处。由于绝缘缺陷或者人为误操作，开关柜内部也会产生故障燃弧现象，对设备和操作人员的人身危害巨大。研究和控制故障燃弧过程的电弧形态，对减少故障燃弧所接触的面积，减少故障燃弧带来的损失、抑制因故障燃弧引起的大面积故障有重要的意义。

基于电极形状对故障电弧形态的影响，采用仿真与实验结合的方法，研究了杯状电极下直流10 kA故障电弧的发展和稳定燃烧的状态，分析其形状成因。首先在有限体积法的基础上，通过磁流体动力学模型[3-4]结合湍流模型、辐射模型，完成多物理场耦合的大电流直流电弧仿真计算、数值计算获得杯状电极间的电弧的温度、压力等分布参数，然后对比仿真结果与实验结果，验证仿真的有效性从而获得电弧的形态发展过程和最终燃弧状态，为电器制造行业设计提供指导。

1 实验电路及电极模型

实验电路如图1所示，电路为简单的直流回路，由高压直流源、开关、电极和电阻组成，其中电极放置在实验腔体内。

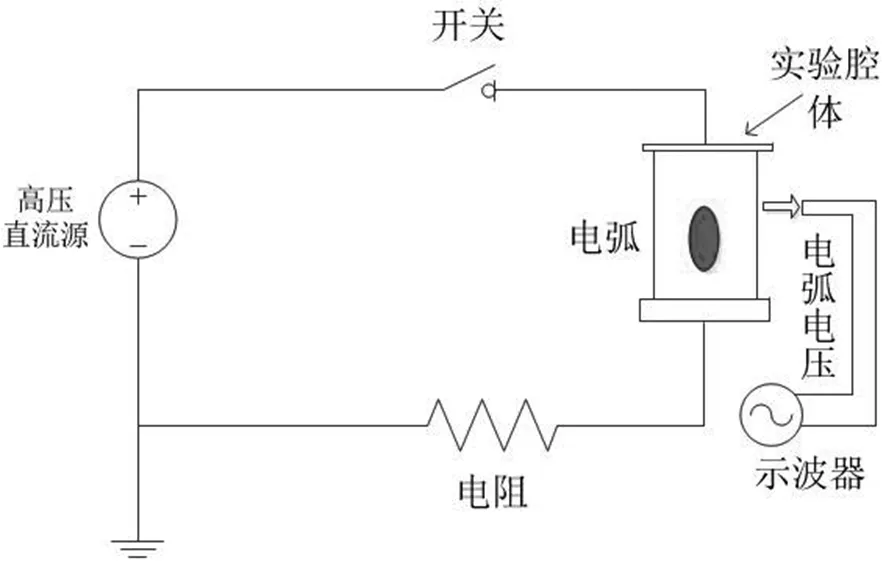
图1 实验电路图Fig.1 Experimental circuit diagram

杯状电极结构及其燃弧区域如图2所示。杯状电极有凹槽部分和外沿部分，杯状电极的外径为50 mm，内径为30 mm，高为50 mm，极间距为30 mm。

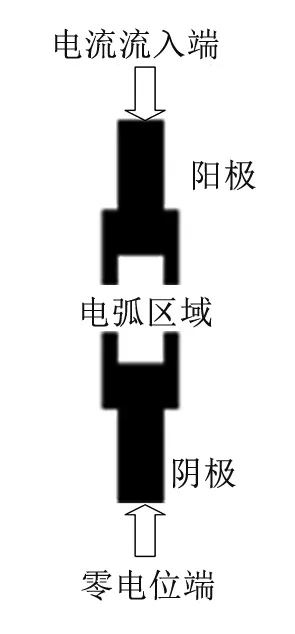
图2 电极结构示意图Fig.2 A schematic view of the electrode structure

实验时，在电极间接入细小铜丝，细小铜丝在大电流的作用下熔化开断形成电弧，施加电流为10 kA。进行电弧的数值仿真计算前，需在物理模型的基础进行网格剖分，生成计算所需的网格模型，对于电极间的电弧核心计算区域，需要进行网格局部加密，以适量降低计算收敛的难度。

2 数学模型建立

2.1 模型假设

空气电弧的物理化学过程非常复杂，为了减小仿真计算的复杂度，引入一些合理的假设[5-8]：首先，空气电弧等离子体满足局部热力学平衡条件；其次，仿真中不考虑电弧对电极的烧蚀作用。

2.2 控制方程

(1)质量守恒方程(连续方程)

(1)

式中，t、ρ、U分别为时间、流体密度、流体运动的速度矢量。

(2)动量守恒方程

(2)

(3)能量守恒方程

(3)

式中h、λ、cp、Sh分别为焓、热导率、定压比热、能量源相。

(4)电磁场控制方程为磁矢位方程[9]

B=×A

(4)

E=-φ

(5)

(6)

(7)

式中A、φ分别为磁矢位、电位。

(5)辐射方程

采用的辐射模型为简化T4法，利用黑体辐射的斯蒂芬-玻尔兹曼定律[10]进行辐射能量的计算，定律中黑体的总发射能量与黑体热力学温度的4次方成正比，表示为

(8)

式中α、k、T、T0分别为斯蒂芬-玻尔兹曼常数、吸收系数、电弧温度和环境温度。

2.3 边界条件

(1)温度边界

非金属壁面的温度软件设为一维导热方程。

(9)

式中q、qrad、λw、d分别为器壁出的热流密度、辐射热、器壁材料的导热率和器壁厚度。

(2)压力边界

上下两边与外界相连，设置为压力出口边界条件，出气口面上的压强为大气压强。

(3)电磁场边界

在阳极和阴极导电杆末端界面上设置电场边界，如图2中所示，阳极的导电杆末端设置为电流输入，其电流大小为10 kA，阴极的导电杆末端设置为零点位。建模时导电杆长度较长，电流的输入端界面离电弧区域较远，对于阳极则假定的输入电流密度均匀分布，则给定电流I有

(10)

式中ji、Si、N分别电流密度，阳极输入端上每个单元面的面积和总单元数。

磁场边界设置通过设置边界单元的磁矢位A的值来实现，对于边界单位的磁矢位设置为0。

3 仿真结果分析

3.1 温度分布

电极间的电弧温度分布随时间变化如图3所示，从电极间的电弧温度分布可见，电极间的电弧经历了膨胀扩散到稳定燃烧程。

图3 极间电弧的温度分布Fig.3 Arc temperature distribution between arc electrodes

在1.62 ms时刻，电弧的温度场在电极间呈对称分布，核心最高温度在20 000 K左右并沿电极横向对称轴向外扩散；到3.89 ms时，电弧的温度场开始呈现向上扩散的趋势；4.19 ms时电弧的高温区域到达阳极的外沿部分，该处空气电导率上升，极小部分电流开始从阳极外沿部分经电弧高温区域到达阴极；4.59 ms时阳极处电流完成从阳极凹槽底部向路径更短的阳极外沿转移，阳极凹槽处不再是电弧高温区域；从5.59 ms到12.59 ms的温度场分布可以得到，阳极凹槽处的温度分布经历由低温到再次充满高温气体的一个过程，部分电流再次流经阳极凹槽底部，该过程较电流从阳极凹槽转移到阳极外沿过程要缓慢的多，最后电弧呈现出阴极收缩，阳极扩张的形态稳定燃烧，从起弧到稳定燃烧的过程历时十几个毫秒。

3.2 气压分布

电极间的气体压力分布随时间变化如图4所示，其值为表压。气压分布的变化与温度分布的变化相对应。从图中，我们可以发现3.89 ms到4.59 ms的时间内，气压变化的过程最为激烈，这与电弧在该段时间内的形态变化相关；在时刻4.59 ms后，电极间的气压分布形态在电极间靠近阳极处维持一个锥形的高压区域，该高压区域在一定程度阻止了电弧高温气体向阳极凹槽处扩散，电弧进入一个缓慢的趋向稳定燃烧的过程，直至稳定燃烧。

图4 极间电弧气体压力分布Fig.4 Arc gas pressure distribution between electrodes

3.3 气流场速度分布

图5为4.59 ms和26.59 ms时刻的电极间电弧气流场速度的矢量分布图，图5(a)与图4中4.59 ms时刻的气压分布相吻合，由于锥形高压区域的存在，电弧气流由中心向两边分流，将高温气体吹向阳极的两侧，高温气体无法到达阳极凹槽底部，阳极凹槽底部温度较低，与图3中的4.59 ms时刻的温度分布相吻合。

图5(b)的气流场速度分布是稳定燃弧阶段的气流场，该时刻的锥形高压的气压值相对较小，高温气流能够到达阳极凹槽底部，阳极凹槽底部充满高温气体，温度升高凹槽处电导率上升，部分电流流经阳极凹槽底部，电弧到达稳定燃烧的状态，电弧的温度场、气流场和气压场维持一个相对稳定的状态。

图5 不同时刻电极间的速度场Fig.5 Velocity field between electrodes at different time

3.4 仿真电弧分析

从仿真结果分析可得，杯状电极间的故障燃弧经历了膨胀到稳定燃烧的过程，稳定燃烧的电弧呈现阴极收缩阳极扩张的状态，且电弧阴极弧根处于电极凹槽底部，在多物理场的作用下，高温气体由阴极吹向阳极并在靠近阳极处向两边分散，杯状电极间的电弧固定在电极间而不向外部运动。

4 仿真有效性评估

为了验证仿真模型的有效性，将仿真数据与实验数据进行对比。实验中，电弧开断过程中电弧的温度分布、气压分布和气流场分布难以直接测量到，电弧区域的各物理场分布会直接影响电弧区域的电导率，电导率随电弧的发展过程时刻变化，而电导率大小直接影响电弧电压大小，因此比较电弧电压可以直观反映仿真模型是否正确。

实验数据的获得如图1中所示，通过示波器记录电弧电压，将收集到的电压数据与仿真得到的电压数据进行对比并在同一表格中显示，如图6所示。

图6 电压曲线Fig.6 Voltage curve

从图6可见，两条电压曲线的趋势是一致的，在起弧几个毫秒后电弧电压开始下降，在10 ms后仿真电弧电压和实验电弧电压值基本都稳定在130～140 V之间。实验测得的电弧电压曲线尽管有波动，但都围绕着仿真电弧电压上下波动，因此，所建立的仿真模型有效。

5 结论

针对杯状电极间10 kA直流电弧，完成了基于磁流体动力学模型的电弧数值仿真计算，得到了实验无法获得的电弧温度分布、气压分布以及气流场速度的矢量分布，研究杯状电极间电弧的发展过程和稳定燃烧的形态，通过实验验证，证明仿真模型有效，所得结论如下：

1)证明数学模型的假设和数学控制的控制方程合理，数值计算的电压与实验电压相一致。

2)在杯状电极间的电弧形状呈现阴极收缩，阳极扩张的状态，且阴极的弧根处于凹槽底部而非路径更短的外沿处；阳极则凹槽处和外沿处充满高温气体，呈现弥散的状态。

3)电弧稳定燃烧后，核心电弧高温区域仅分布在电极间区域。