非线性矩阵方程双对称解的牛顿-MCG算法

(福建工程学院 应用技术学院，福建 福州 350000)

双对称矩阵在信息理论、马尔可夫过程、物理工程等领域中有广泛应用，很多学者研究了矩阵方程(组)的双对称解问题[1-9]。在控制理论、随机滤波分析[10-12]等领域，会遇到形如求矩阵方程

X+E1X-1F1+E2X-2F2+E3X-3F3=G(1)

的特殊解问题，其中Ei,Fi,G,X∈Rn×n(i=1,2,3)。本文拟用牛顿-修正共轭梯度算法(牛顿-MCG算法)求解矩阵方程(1)的双对称解。

1 求解方程(1)双对称解的牛顿算法

定义1划分n阶单位矩阵I=(e1,e2,…,

en)，称Sn=(en,en-1,…,e1)为n阶次单位矩阵。若X∈Rn×n满足SnXSn=X且XT=X，称X为双对称矩阵，用BSRn×n表示双对称矩阵集合。

令X=X-1,则方程(1)可以改为

X-1+E1XF1+E2X2F2+E3X3F3=G

为了方便书写，引入下列矩阵函数：

因为

E3(XYX+X2Y+YX2)F3-X-1YX-1

所以记

E3(XYX+X2Y+YX2)F3-X-1YX-1

E3(XY2+Y2X+YXY+Y3)F3

容易导出

ψ(X+Y)=ψ(X)+φX(Y)+γX(Y)

(2)

这里φX(Y)是ψ(X)在“点X”沿着“方向Y”的Frechet导数。

引理1[8]设X∈BSRn×n是方程(1)的近似解，则求方程(1)双对称解X可转化为求校正值Y∈BSRn×n使得ψ(X+Y)=O，并可以线性化为求Y∈BSRn×n使得

φX(Y)=-ψ(X)

(3)

在引理1中，φX(Y)=-ψ(X)的解Y∈BSRn×n一般不是ψ(X+Y)=O的精确解，从而由X*=X+Y确定的X*∈BSRn×n也不是ψ(X)=O的精确解，但是可以看作一个近似解。借鉴牛顿算法的原理，建立求方程(1)双对称解的牛顿算法如下：

第1步：给定矩阵X(k)∈BSRn×n，置k∶=1。

第2步：若ψ(X(k))=O，计算停止；否则，求Y(k)∈BSRn×n，使得

φX(k)(Y(k))=-ψ(X(k))

第3步：计算X(k+1)=X(k)+Y(k)，置k∶=k+1，转第2步。

文献[13]中给出了关于牛顿迭代法求非线性矩阵方程的收敛性结论：假设X*是方程(3)的解，则由牛顿算法生成的矩阵序列{X(k)}收敛于X*。此外，牛顿算法的关键是求解线性矩阵方程(3)。但由于截断误差的存在，对牛顿法中的某个迭代步k，矩阵方程(3)可能没有双对称解，此时可求它的最小二乘双对称解，这也是牛顿-MCG算法的一个特点。

2 求线性矩阵方程(3)双对称解的MCG算法

记

A1=E1,B1=F1,A2=E2X,B2=F2,A3=E2,B3=XF2，

A4=E3X,B4=XF3,A5=E3X2,B5=F3,A6=E3,B6=X2F3，

A7=-X-1,B7=X-1,F=-(X-1+E1XF1+E2X2F2+E3X3F3-G)

下面建立求方程(3)双对称解和最小二乘双对称解的MCG算法，考虑方程(3)的一般形式

(4)

其中Ai,Bi,Ci,Di,F∈Rn×n(i=1,2,…,7)。

问题Ⅰ当方程(4)有双对称解时，求Y∈BSRn×n，使其满足方程(4)。

问题Ⅱ当方程(4)无双对称解时，求Y∈BSRn×n，使得

(5)

当方程(4)有双对称解时，称问题Ⅰ相容；否则称问题Ⅰ不相容。

参考文献[8]的算法原理，通过修改矩阵Qk的类型，在共轭梯度法的基础上建立求解问题Ⅰ的MCG算法如下。引入记号：

算法1(求解问题I的MCG算法)

第1步：任意给定初始矩阵Y(k)∈BSRn×n，置k∶=1，计算

第2步：如果Rk=O，或者Rk≠O而Qk=O，则停止计算；否则计算

第3步：计算

βk+1Qk

第4步：置k∶=k+1，转第2步。

显然，算法1中的矩阵Y(k),Qk∈BSRn×n。下面给出算法1的基本性质，证明算法1在有限步计算之后停止，具体证明过程参考文献[14]。

性质2设k≥2，对算法1中的矩阵Ri和Qj，有

定理1设问题Ⅰ有双对称解，任意给定初始矩阵Y(1)∈BSRn×n，算法Ⅰ可在有限步计算后求得问题Ⅰ的一组解。问题Ⅰ无双对称解的充要条件是存在正整数k，使得在算法1得到的Rk≠O而Qk=O。

定理2设问题Ⅰ有双对称解，选取初始矩阵Y(1)∈BSRn×n如下

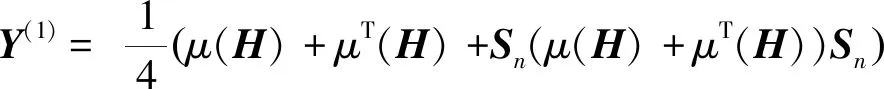
(∀H∈Rn×n)

则在有限步迭代计算后可得问题Ⅰ的唯一极小范数解。

3 求解问题Ⅱ的MCG算法

根据定理1，在算法1中，当Rk≠O而Qk=O时，算法1中断，表明线性方程(4)无双对称解，需要求解方程(4)最小二乘双对称解。下面把问题Ⅱ的求解转化为求解等价正规方程双对称解问题。参照算法1，建立求方程(4)最小二乘双对称解的迭代算法。

引进记号：

f(Y)=w(μ(Y))+[w(μ(YT))]T+

Sn(w(μ(SnYSn))+[w(μ(SnYTSn))]T)Sn

N=w(F)+[w(F)]T+Sn(w(F)+[w(F)]T)Sn

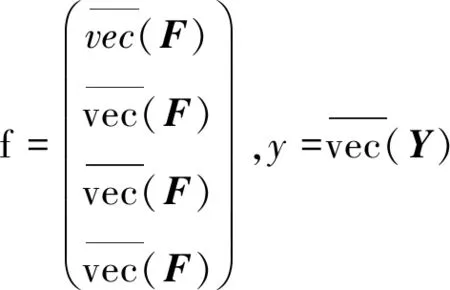
定理3问题Ⅱ的解等价于线性矩阵方程f(Y)=N的双对称解，而且此线性矩阵方程必有双对称解。

证 问题Ⅱ的求解等价于求Y∈BSRn×n，使得

(6)

下面证明求极小值问题(6)等价于求矩阵方程f(Y)=N双对称解。将矩阵方程组

(7)

参照算法1以及文献[11]的算法原理，建立求矩阵方程f(Y)=N双对称解，即求解问题Ⅱ的MCG算法如下。

算法2(求解问题Ⅱ的MCG算法)

第1步：给定矩阵Y(k)∈BSRn×n，置k∶=1，计算

第2步：若Rk=O，则停止计算；否则计算

第3步：计算

第4步：置k∶=k+1，转第2步。

易见，在算法2中矩阵Y(k),Qk∈BSRn×n，对于算法2有类似于算法1的收敛定理。

定理4给定初始矩阵Y(1)∈BSRn×n，算法2在有限步迭代计算后可得问题Ⅱ解，即矩阵方程(4)最小二乘双对称解。

4 数值算例

下面给出两个算例，在例1中，通过改变矩阵的阶数，说明文中建立的算法1和算法2是可行的，且具有很高的效率。在例2中，通过和文献[15]的算法(简称Li算法)作比较，说明本文中建立的牛顿-MCG算法适用范围更广，且能求出此类矩阵双对称约束解。用t表示计算时间(s)、n代表矩阵的阶数、k1代表算法1迭代次数、k12代表算法1中断次数、k2代表算法2迭代次数、error代表实际误差的范数。

采用如下计算步骤：

第1步：给定矩阵X(1)∈BSRn×n，置k∶=1。

第2步：若ψ(X(k))=O，计算停止；否则，采用算法1求矩阵方程(4)的双对称解；若方程(4)无双对称解，则采用算法2求Y(k)∈BSRn×n，使得

‖φX(k)(Y(k))+ψ(X(k))‖=min

第3步：计算X(k+1)=X(k)+Y(k)，置k∶=k+1，转第2步。

例1 用本文建立的算法1和算法2求矩阵方程(1)的一组双对称解和最小二乘双对称解，取方程(1)系数矩阵均为n阶方阵，系数矩阵、终止准则如下：

E1=E2=F1=F2=I，E3=-2IT,F3=2I，G=I，X1=I，ε=10-9(终止准则)，

选取初始矩阵Y1=O，按计算步骤求得矩阵方程(1)的双对称解，结果如表1(MATLAB软件2014版-PIV3.0 GHz微机)。

表1 方程(1)的双对称解计算结果

当n=4时，可得矩阵方程(1)的双对称解为

例2 用本文算法1、算法2和文献[15]的Li算法求方程(1)的特例X-A*X-3A=Q，取该特例方程系数矩阵、初始矩阵X1、终止准则如下：

A=I，G=I，X1=I，ε=10-9(终止准则)，

(1)选取初始矩阵Y1=O，按照算法1和Li算法求阵方程X-A*X-3A=Q的一组双对称解，结果如表2。

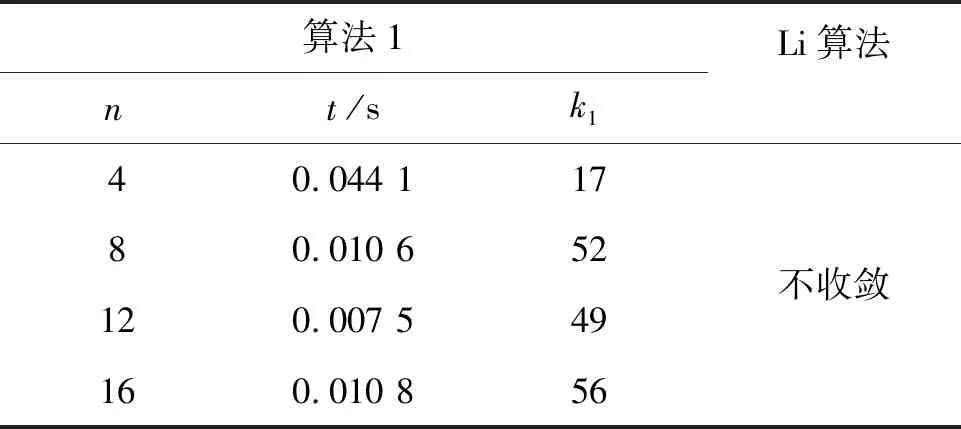
表2 算法1与Li算法比较结果

(2)当矩阵G为元素全为1的n阶方阵时，文献[15]中的Li算法失效，因为矩阵G不正定，不满足文献[15]中算法条件。但本文中的牛顿-MCG算法有效，能求出方程(1)的双对称解，结果如表3。

从表1可以看出，算法1和算法2求解矩阵方程(1)是有效的，当方程(1)有双对称解时，可以求出其双对称解。当算法1中断时，可以通过算法2计算方程(1)的最小二乘双对称解。从表2，3可以看出，与文献[15]中的Li算法比较，本文建立的牛顿-MCG算法适应范围更广，能求出矩阵方程(1)特例方程的双对称解。

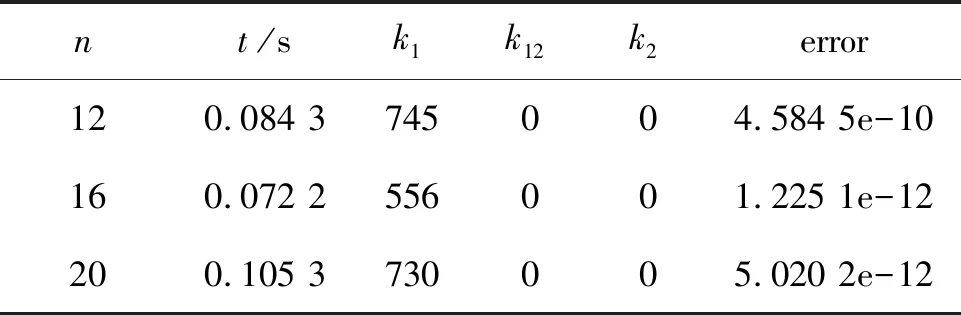
表3 牛顿-MCG算法求方程(1)特例的双对称解计算结果

5 结论

本文建立基于牛顿算法和共轭梯度算法原理建立的单变量非线性矩阵方程(1)双迭代算法，文中采用的MCG算法不同于通常的共轭梯度法，它不要求涉及的等价线性矩阵方程(3)的系数矩阵对称正定、可逆或者列满秩，因此总是可行的。本文建立的迭代算法仅要求方程(1)有双对称解，不要求方程(1)的双对称解唯一，也不要求由牛顿算法每一步迭代计算导出的矩阵方程有双对称解。将牛顿-MCG算法运用于其他非线性矩阵方程，这是下一步的研究的重点。