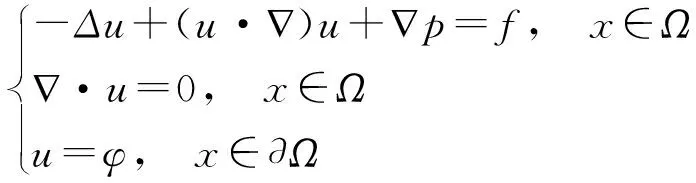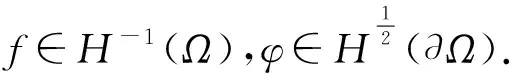千禧问题之一: 不可压缩Navier-Stokes方程
韩丕功
(1. 中国科学院 数学与系统科学研究院, 北京 100190; 2. 中国科学院大学 数学科学学院, 北京 100049)
1 历史背景
下述三维不可压缩Navier-Stokes方程描述了黏性不可压缩流体的运动规律.
(1) ∂tu-νΔu+(u·)u=-p+f, (x,t)∈3×(0,T),
其中ν>0表示流体的黏性系数,u=(u1,u2,u3)(x,t),p=p(x,t)分别表示流体运动在时空点(x,t)处的速度场和压强,f表示给定的外力向量场函数. 方程(1)~(2)分别表示Newton流体力学的动量守恒和质量守恒(即不可压缩条件). 在恒温的情况下, 若速度场适当光滑, 利用方程(1)~(2), 可以推导出不可压缩流体的能量守恒方程, 即能量守恒是动量守恒和质量守恒的推论. 这些方程建立了流体的粒子动量的改变率(加速度)和作用在液体内部压力的变化和耗散黏滞力(产生于分子的相互作用)以及引力之间的关系.
1821年, 法国桥梁工程师Navier在讲授工程学和应用数学时, 开始思考与流体有关的数学问题. 1827年, 他以适当分子模型为基础, 只考虑了不可压缩流体的流动, 建立了一个方程, 不幸的是, Navier的数学推导很快被发现有缺陷, 但是基于工程师的直觉, Navier最后的结论依然正确. 随后, 由于Poisson (1831年提出可压缩流体的运动方程), de Saint Venant, 特别是Stokes等独立提出黏性系数为一常数的形式, 他们以连续介质力学为基础, 给出了正确的推导. 在推导过程中, 他们对流体作了几个假设. 第一个假设是流体是连续的. 这强调它不包含形成内部的空隙, 例如, 溶解的气体气泡, 而且它不包含雾状粒子的聚合. 第二个假设是所有涉及到的场, 全部是可微的, 如压强、速度、密度及温度等. 此外, 控制体积可以在空间中固定, 也可能随着流体运动. 这个方程组被后人合称为Navier-Stokes方程. 图1生动地表示出Navier-Stokes方程导出的过程(根据牛顿(Newton)第二定律).
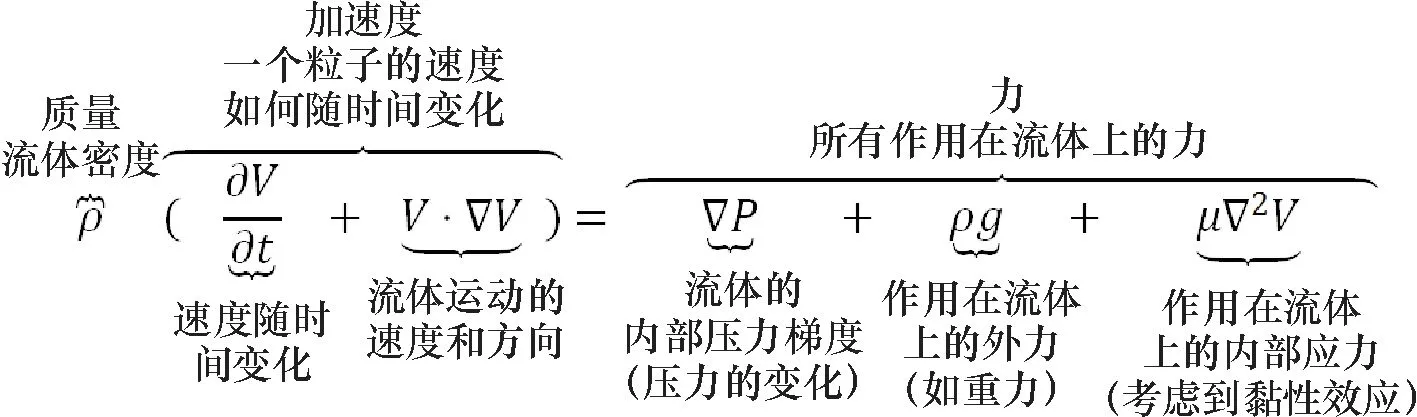
图1 牛顿(Newton)第二定律导出Navier-Stokes方程的过程
Fig.1 The process of Navier Stokes equation derived from Newton’s second law
通常情况下, 考虑的流体密度变化不大, 一般假定密度不变, 即密度为常数. 当时没人了解这个方程的重大意义, 直到一百多年后, 人们才意识到: 这个方程从诞生起, 就开启了一个新的时代.
到了19世纪末, 人们终于开始触及流体运动最核心的本质, 关于流体运动(Navier-Stokes方程)的完整理论开始初步形成. 从理论上讲, 有了包括Navier-Stokes方程在内的基本方程组, 再加上一定的初始条件和边界条件, 就可以确定流体的流动. Navier-Stokes方程是由一组二阶非线性非标准抛物型和一阶椭圆型偏微分方程组成的混合型方程组, 方程组本身不能做任何的改动, 求解非常困难和复杂, 求出该方程的精确解是几乎不可能的, 在求解思路或技术没有进一步发展和突破前, 只有在某些十分简单的特例流动问题上才能求得其精确解. 例如, 求得精确解的最简单情况是平行流动, 这方面代表性的流动是圆管内的哈根-泊肃叶(Hagen-Poiseuille)流动和两平行平板间的库埃特(Couette)流动. 此外, 在部分情况下, 可以简化方程而得到近似解. 例如,当雷诺数(Reynolds number)充分大时, 绕流物体边界层外的黏性力远小于惯性力, 此时方程中黏性项可以忽略, 将Navier-Stokes方程简化为理想流动中的欧拉(Euler)方程; 而在边界层内, Navier-Stokes方程又可简化为边界层方程等. Navier-Stokes描述了大量对学术和经济有用现象的物理过程, 特别是在计算机问世和迅速发展以来, Navier-Stokes方程的数值求解有了较大的发展, 人们不仅能准确地制作出天气预报, 还可以在飞行器和车辆的设计、血液循环的研究、电站的设计、污染效应的分析, 以及在生活、环保、火箭发射、航空航天、国防军工、石油勘探、水利工程、电气工程, 甚至医疗器械等方面都发挥了中流砥柱的作用. Navier-Stokes方程现已成为非线性偏微分方程、数值分析和动力系统研究的推动力量, 是当今非线性科学研究中的重点和热点问题.
Navier-Stokes方程概括了黏性不可压缩流体流动的普遍规律, 因而在流体力学中具有特殊意义. 自然界中大量的流体模型, 例如,具有热传导效应的流体动力学模型、磁流体动力学模型、海洋动力学模型以及描述血液在动脉和静脉中的流动等管道流的数学模型, 其主部均为Navier-Stokes方程. 尽管Navier-Stokes方程已经被提出近两百年, 但是数学上却一直无法找到它的精确解. 目前取得的重大科技突破都源自于计算机的近似模拟计算, 因此, 破译Navier-Stokes方程解的密码将带来对流体运动本身最深刻的认知, 从而推动科技文明跨入新的时代. 正如一篇散文里所写, 起伏的波浪跟随着正在湖中蜿蜒穿梭的小船, 湍急的气流跟随着现代喷气式飞机的飞行. 数学家和物理学家深信, 无论是微风还是湍流, 都可以通过理解Navier-Stokes方程的解, 来对它们进行解释和预言. 虽然Navier-Stokes方程是19世纪写下的, 笔者对它们的理解仍然极少. 挑战在于对数学理论作出实质性的进展, 以能解开隐藏在Navier-Stokes方程中的奥秘.
美国Clay研究所在2000年把三维不可压缩Navier-Stokes方程具有有限能量光滑初值整体正则解的存在性或在有限时间内爆破列为七个“千禧难题”(又称世界七大数学难题)之一. 2002年, Fefferman专门为这个千禧难题作了介绍和评论, 并断言: 如果没有新的分析工具和数学思想, 这个问题是很难完全解决的. 此外, Smale (Fields奖得主)均把该模型作为本世纪需要解决的重大问题之一.
“研究三维不可压缩Navier-Stokes方程光滑解的整体存在性和稳定性, 为航空航天飞行器、外形气动布局、气候异常环流解、海洋层流的运动等科学问题研究提供理论基础. ”(摘自国家数学交叉中心网站)
李大潜等在《物理学与偏微分方程》专著中写道:“Navier-Stokes方程是一个相当复杂的非线性方程组, ……, 具有极大的重要性, ……. 预期在今后相当长的一段时间内, 无论在理论上还是在数值解法上, 都将是非常热门的研究对象.”
目前, 国际上许多著名数学家都对Navier-Stokes方程进行了广泛深入的研究, 获得了许多丰富的、重要的成果. 例如,Caffarelli (美国科学院院士, Wolf奖得主), Fefferman (美国科学院院士, Fields奖得主), Lions (法国科学院院士, Fields奖得主), Nirenberg (美国科学院院士, Abel奖得主), Temam (法国科学院院士), Tao (Fields奖得主), Giga (ICM45分钟报告), Schonbek (美国), Sohr (德国)等.
2 存在性
笔者首先给出几类弱解的定义. 考虑Navier-Stokes方程的Cauchy问题(n≥2):
(1)

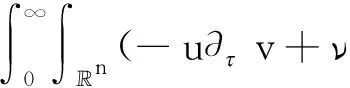
(u·)u·v)(x,)dxd=
如果弱解u满足下述能量不等式, 即对几乎处处的时间t∈[0,∞), 包括t=0, 成立
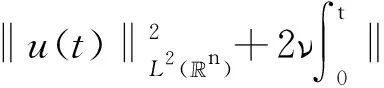
则称u为问题(1)的Leray-Hopf弱解.
如果弱解u满足强能量不等式, 即对于几乎所有的s≥0, 包括s=0, 以及所有的t≥s, 成立
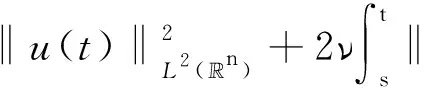
则称u为问题(1)的湍流解(turbulent solution).
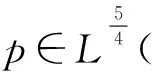
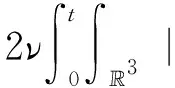
(|u|2+2p)u·φ)dxd+
则称(u,p)为问题(1)的适当弱解(suitable weak solution).
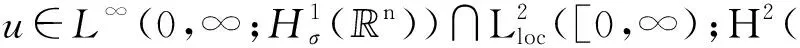
关于不可压缩Navier-Stokes方程的Cauchy问题, 真正系统的数学理论研究始于20世纪30年代. Leray[1]在1934年的开创性工作中, 建立了黏性不可压缩流体力学的数学理论基础. Leray首次构造了在二维、三维情形下, 问题(1)存在具有有限能量的一类整体弱解,并且当初始向量函数光滑时, 存在常数T0≥δ>0, 使得弱解在时间区间(0,δ)∪(T0,∞)内是光滑的. Leray还进一步分析了他所构造的弱解u关于时间的可能奇异点集合的Hausdorff测度估计, 即
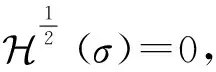
1951年, Hopf[2]证明了问题(1)在三维情形下具有有限能量整体弱解的存在性. 因此,Navier-Stokes方程的弱解通常也称之为Leray-Hopf弱解.
Temam[3]在其专著中, 利用Galerkin方法、弱收敛定理和紧性理论, 也证明了问题(1)在二、三维情形下存在整体弱解且满足能量不等式, 即Leray-Hopf弱解的存在性.
1984年, Kato[4]利用Picard序列方法, 假定初始函数u0在L3范数意义下比较小, 证明了问题(1)在三维情形下存在整体光滑解(关于时空变量), 也就是通常所说的Navier-Stokes方程的Cauchy问题存在整体光滑的小解.
3 正则性
迄今为止, 在三维情形下, 尽管已有很多重要的结果, 但是问题(1)的Leray-Hopf整体弱解的正则性仍然不清楚, 目前仍然是流体力学理论中的一个基础性的公开问题.
Foias[5]、Lions等[6]、Prodi[7]和Serrin[8-9]对n维Navier-Stokes方程Cauchy问题的Leray-Hopf弱解u的正则性进行了系统的研究, 建立了如下正则性准则, 即
如果u∈Ls(0,∞;Lq(n)),其中,
(2)
则u关于时空点(x,t)是光滑的, 即u∈C∞(n×(0,∞)), 这里n≥2.
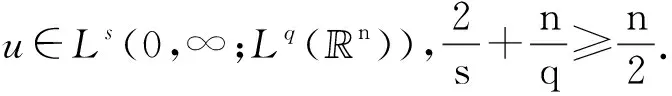
需要指出的是, 如果Leray-Hopf弱解u在端点空间L∞(0,T;L3(3))中, 长期以来一直都不清楚u是否是正则的. 2003年, 利用抛物方程的倒向唯一性定理和连续性方法, 在L∞(0,T;L3(3))中, Escauriaza等[11]证明了Leray-Hopf弱解u的正则性, 当然也是唯一的. 这在Navier-Stokes方程解的正则性研究方面是一个重要的进展和突破, 即
如果u∈L∞(0,T;L3(3)),则u∈C∞(3×(0,T)).
Escauriaza等[11]在建立上述正则性的过程中, 所用的创新方法主要是爆破分析技巧和下面两个重要的引理.
引理1 (Backward uniqueness) 记QR=(3BR(0))×(-1,0),R>0. 假定u,∂tu,2u∈L2(QR)且
(|∂+u(x,t)-Δu(x,t)|≤C1(|u(x,t)|+
|u(x,t)|≤C2eC3|x|2, ∀(x,t)∈QR;
u(x,0)=0, ∀x∈3BR(0).
则u(x,t)≡0,∀(x,t)∈QR.
注在上述引理1中不需要边值条件.
引理2(Unique continuation) 记DR=BR(0)×(-1,0),R>0. 假定u,∂tu,2u∈L2(DR)且
(|∂+u(x,t)-Δu(x,t)|≤C4(|u(x,t)|+
u(x,t) (|x|2-t)-k∈L∞(DR), ∀k∈,
则u(x,t)≡0,∀(x,t)∈BR.
关于三维不可压缩Navier-Stokes方程, Scheffer[12-14]从1976年起发表了一系列论文, 开始研究适当弱解的奇异点集合的结构, 即部分正则性问题. 这里称时空点(x,t)是可测函数v的奇异点, 是指在(x,t)的任何一个小邻域Q上, ‖v‖L∞ (Q)=∞. 反之, 时空点(x,t)为函数v的正则点.
设(u,p)满足Navier-Stokes方程(经典或广义意义下). 令
uλ(x,t)=λu(λx,λ2t),pλ(x,t)=λ2p(λx,λ2t),
则(uλ,pλ)满足Navier-Stokes方程. 这是不可压缩Navier-Stokes方程本身具有的独特性质——伸缩不变性. 充分利用这一伸缩不变性, Caffarelli等[15]在1982年证明了适当弱解的奇异点集的一维Hausdorff测度为零, 这是一个极为深刻的结果, 首次揭示了所有可能的时空奇异点只能分布在一根时空轴线上. 到目前为止, 这是关于部分正则性问题方面最好的研究结果. 需要说明的是, 在文献[15]里, 定义了一类适当弱解, 他们在有界区域上, 利用磨光函数的性质, 还证明了这类整体适当弱解确实是存在的. 确切地讲, 记Qr=Qr(x0,t0)为时空点(x0,t0)的抛物邻域, 即
Qr={(x,t)∈3×(0,∞)│|x-x0|<
r,t0-r2 假定X⊂3×1,k为非负整数. 定义(详情见文献[15]) 其中 可知Fk是正则的Borel测度. Hausdorff测度Hk也是用类似的方式定义, 只是在上述定义中的Qri被3×1中任意的闭子集合(其直径不超过ri)代替. 显然,k≤C(k)k. 记S⊂3×(0,∞)为三维Navier-Stokes方程适当弱解的所有可能的时空奇异点构成的集合. Caffarelli等[15]证明了1(S)=0. 注关于三维Navier-Stokes方程正则性研究, 相对于文献[15]的结果, Tian等[16]在1999年给出了一些新的充分必要条件(在伸缩不变意义下). 例如, 其中一个假设条件是弱解旋度的局部L2范数适当小, 另外一个是速度场的局部L2行为小条件假设. Lin[17]在1998年利用调和函数的性质, 极大地简化了Caffarelli-kohn-Nirenberg的证明过程, 得到了同样的正则性结果. Constantin等[18]在1993年给出了一个几何正则性准则, 即如果旋度比较大时, 旋度的方向是Lipschitz连续的, 则Leray-Hopf弱解是正则的. 具体表述如下: 记ω=×u表示速度场u的旋度,表示向量ξ(x+y,t)在向量ξ(x,t)的垂直方向上的投影. 假定存在常数Ω>0和ρ>0, 使得如果|ω(x,t)|>Ω和|ω(x+y,t)|>Ω,x,y∈3,0≤t 则Navier-Stokes方程的Leray-Hopf弱解u在3×(0,T)上光滑的. 下面简单介绍Navier-Stokes方程自相似解方面的研究结果, 这也是Leray[1]在1934年的论文中关注的一个重要问题. 假定(u,p)是三维Navier-Stokes方程的解, 则(ul,pl)也满足Navier-Stokes方程(方程的伸缩不变性), 这里 ul(x,t)=l-1u(xl-1,tl-2),pl(x,t)= l-2p(xl-1,tl-2). 如果成立: (u,p)=(ul,pl),∀l>0, 则称(u,p)是Navier-Stokes方程的自相似解. 容易验证自相似解(u,p)可以写成如下形式: u(x,t)=λ(t)U(λ(t)x),p(x,t)= 这里U(y)=(U1,U2,U3)(y),P(y)定义在3上, 且满足如下椭圆方程: -ΔU+aU+a(y·)U+(U·)U+ 1934年, Leray[1]提出Navier-Stokes方程的自相似解问题. 三维Navier-Stokes方程是否存在具有整体有限能量的自相似弱解? 即是否存在自相似弱解u, 满足如下有限能量 1996年, Necas等[19]证明: 如果U∈L3(3), 则U≡0. 该结论表明: 三维Navier-Stokes方程具有有限能量的自相似解只能是平凡解, 从而解决了Leray最初提出的自相似解问题. 这是因为L3(3)在伸缩意义下是不变空间, 即对几乎处处的t>0, 成立‖u(t)‖L3=‖U‖L3. 另一方面, 利用Sobolev嵌入定理和内插不等式, 可知对几乎处处的t>0, 成立u(t)∈L3(3). Tsai[20]进一步证明: 若U∈Lq(3),3 1934年, Leray[1]在其开创性的工作中, 对不可压缩Navier-Stokes方程建立了二、三维整体弱解的存在性, 并首次提出弱解u的能量是否大时间衰减到零? 即当t→∞时, 下述衰减是否成立, ‖u(t)‖L2→0. 这是一个十分困难且极具挑战性的公开问题, 需要新的思想及创新性的方法产生. Leray提出的这个公开问题经过五十余年后才被Schonbek[21], Wiegner[22]和Kajikiya等[23]分别独立解决, 所用方法主要是Schonbek创立的Fourier分离技巧,Wiegner建立的基本不等式以及 Miyakawa等建立的谱分析方法. (1)Schonbek[21]利用Fourier分离技巧(现在也称Schonbek方法), 以及Kajikiya等[23]利用谱分析方法, 分别独立证明了Navier-Stokes方程的Cauchy问题存在Leray-Hopf弱解, 其能量不仅衰减到零, 而且还给出了衰减速率, 即 定理1设u0∈Lσ2(n)(n≥2). 则问题(1)存在Leray-Hopf弱解u, 满足下面性质: (i)当t→∞时, ‖u(t)‖L2(n)→0. 和线性热方程的解eΔtu0比较, 定理1中得到的结果是最佳的. 事实上, 还有如下结果: 定理2如果u是定理1中得到的弱解,则 上述两个定理中的常数C仅依赖于n,‖u0‖L2 (n)和‖u0‖L1 (n),eΔtu0表示具有初值n)的线性热方程的解. (2)Wiegner[22]研究带外力函数的n维不可压缩Navier-Stokes方程Cauchy问题湍流解(自然也是Leray-Hopf弱解)的能量衰减估计, 即 (3) 其中,f=f(x,t)表示给定的外力场函数. Wiegner[22]首先建立了如下基本不等式: 假设u是上述问题(3)的湍流解. 则存在固定常数Cn>0, 使得对于任何函数g∈C([0,∞),+),t≥0, 成立 其中, 这里u0(t)表示具有相同初值条件(a,f)的热传导方程组的解, 即 利用上述基本不等式, 结合一些积分不等式, Wiegner[22]对任意的湍流解(自然也是Leray-Hopf弱解)建立了最优的L2-大时间衰减速率, 即 (2)进一步假定 ‖u0(t)‖L2(n)+(1+t)‖f(t)‖L2(n)≤ 则对任意的t≥0, 成立 (3)对任意的t≥0, 成立 注假定f≡0,a∈L1(n)∩Lσ2(n). 由卷积形式的Young不等式可知, ‖u0(t)‖L2(n)=‖etΔa‖L2(n)≤ (3)′‖u(t)-u0(t)‖L2(n)≤ 注和线性热方程基本解比较, 结合(3)′中的结论, 可知上述(2)′中的衰减速率是最优的. Schonbek[24]还进一步系统地研究了Leray-Hopf弱解的L2下界大时间渐近行为, 给出了很多深刻的结论; Borchers等[25-26]分别在经典的上半空间和外区域上建立了Leray-Hopf弱解的L2(上界)大时间渐近行为, Stokes算子在这两类经典区域上生成有界的解析算子半群; 此外, Borchers等[27]利用谱分析方法, 在一般的无界区域上, 给出了Leray-Hopf弱解的L2长时间衰减行为, 这是目前唯一的衰减结果, 主要困难在于不清楚由Stokes算子在一般无界区域上生成的算子半群是否满足Lq-Lr估计, 而Lq-Lr估计是研究Leray-Hopf弱解能量衰减的基本工具. 自从L2的衰减问题解决后, 人们开始在更一般的Lr空间里研究解的大时间渐近行为. 例如, Kato[4]对Navier-Stokes方程的Cauchy问题, 在Lr空间里证明了小初值整体光滑解的存在性, 并给出了Lr长时间渐近行为; Fujigaki等[28]在半空间建立了类似的衰减结果; He等[29-30], Han[31-33]在外区域上建立了各种情形的Lr(包括一、二阶和高阶导数情形)衰减性质. 上半空间作为一类经典区域, 具有特殊的结构. 例如, 平坦结构可以使用广义Fourier 变换作为研究工具. 一般讲, 对于标准的偏微分方程, 其研究(如正则性)都是先把研究的区域, 通过单位分解局部化, 再通过拉伸、旋转等方式(光滑的同构映射)转换为上半空间, 然后再进行分析研究, 最后把半空间上得到的结果再逆同构映射回去. 这种标准的研究方法对Navier-Stokes方程是失效的, 因为Navier-Stokes方程是一类椭圆和抛物组成的混合型方程组. 尽管在上半空间上已有众多的衰减研究结果, 但在端点空间中研究不可压缩Navier-Stokes解的长时间渐近行为一直没有任何结果, 这是一个具有挑战性的困难问题. 主要困难来源于上半空间的边界是非紧的, 通常所用方法在这类空间上不再适用 (如 Stokes算子的Lq-Lr估计在q=r=1时不成立); 同时, 在外区域(边界是紧的)上建立端点衰减结果中所使用的方法, 在研究半空间情形时也是失效的. 近几年, 在半空间情形下, Han[34-36]系统地研究并建立了Navier-Stokes方程的解在L1范数意义下的大时间渐近行为(包括解关于空间变量的一、二阶导数). 所用的研究方法主要是对Navier-Stokes方程的对流项找到了一种新的、有效的分解. 即 P((u·)u)=(u·)∂i∂j(uiuj), 结合Hardy空间, 利用广义Fourier变换、延拓理论等作为基本工具, 最终可以在端点空间中建立期望的衰减结果. 到目前为止, 关于三维Navier-Stokes方程, 还有很多挑战性的公开问题. 考虑如下三维Navier-Stokes方程的初边值问题: (4) 这里Ω是3的区域,ν>0为黏性系数, 0 关于Cauchy问题(4)的Leray-Hopf弱解正则性问题, 美国Clay研究所在2000年将其列为七大千禧问题之一, 悬赏一百万美元. 即三维不可压缩Navier-Stokes方程Cauchy问题具有有限能量光滑初值整体正则解的存在性或在有限时间内爆破. 到目前为止, 该问题仍未得到解决. 该千禧问题的撰写者, Fields奖得主Fefferman在2002年断言: 如果没有新的分析工具和数学思想, 这个问题是很难完全解决的. 当黏性系数ν→0时, 问题(4)的Leray-Hopf弱解uν是否(在某种意义下)收敛到下述Euler方程的解ue: (5) 目前, 上述收敛问题(5)也是一个极具挑战性的公开问题. 1984年, Kato[37]关于上述收敛问题只是给出了一些等价条件. 若Ω=n(n=2,3), 上述结论(5)成立, 见文献[38],n=2;见文献[39],n=3. 当Ω⊂n(n=2,3)为有界区域时, 适当调整Navier-Stokes方程的解uν, Euler方程的解ue满足的边界条件后, 目前已有很多收敛结果. 例如: uν,ue满足边值条件uν,ue|∂Ω=0, 简单的能量估计表明, 结论(5)是正确的. Iftimie等[40]证明: Iftimie等[41]证明了如下收敛速率: 当ν充分小时, 成立 Masmoudi等[42]证明了如下收敛结果: Xiao等[43]给出如下收敛结果: 存在T1≤T(二维情形下,T1=T), 成立 当Ω≠n(n=2,3), 从uν,ue分别满足的边界条件:上推断, 当ν→0时, 会产生边界层, 收敛估计问题(5)应该是不正确的, 详情参见Constantin[44]的综述性文章. 目前的猜测是, 当ν→0时,uν→v+ue(某种意义下), 其中v满足边界层方程. 假定Ω是具有一定光滑性(例如:Ω∈C2,α,0<α<1)的一般无界区域, 研究问题(4)的解在Lr(r≠2)空间范数意义下的大时间渐近行为. 注目前只有r=2情形的衰减结果, 即 Borchers等[27]利用谱分析方法建立的Leray-Hopf弱解的L2衰减结果, 尽管衰减速率不是最优的, 但却是目前唯一的衰减结果. 考虑定常Navier-Stokes方程: (6) 这里Ω是3中的有界区域. 这是Leray[45]在1933年关于定常Navier-Stokes提出的一个公开问题, 到目前为止已有八十余年悠久历史, 至今仍未得到解决, 即著名的Leray问题. 完全解决Leray问题, 需要在理论上有大的突破、方法上有大的创新. 对Leray问题的研究取得任何新的进展, 都具有非常重要的理论意义和实际应用价值, 都会引起国内外同行的极大关注.
4 衰减性
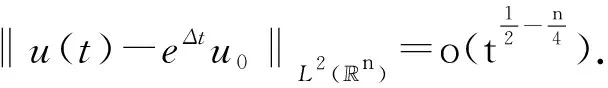
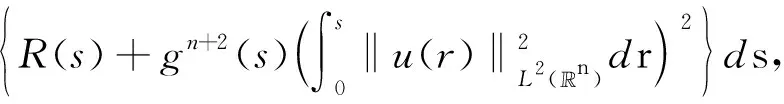
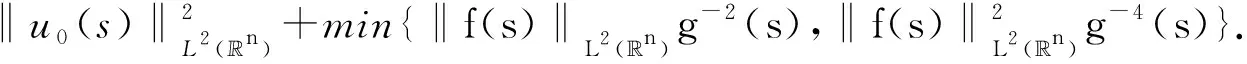
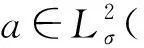
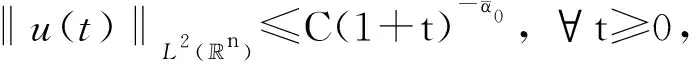
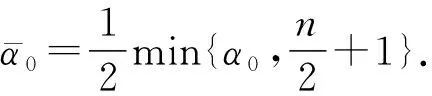
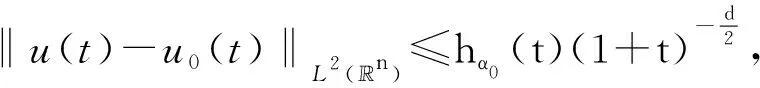
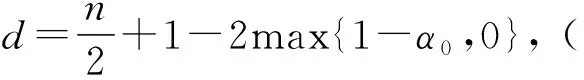
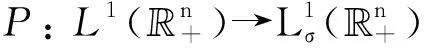
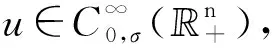
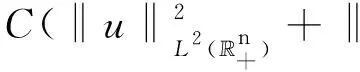
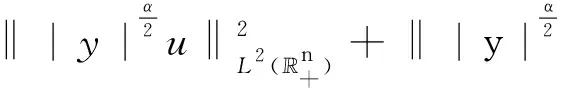
5 一些公开问题
5.1 千禧问题
5.2 黏性系数极限问题

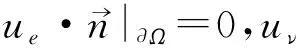
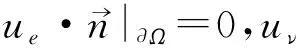
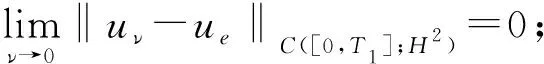
5.3 一般无界区域上的衰减问题
5.4 定常Navier-Stokes方程的Leray问题